Batas trigonometri cara menyelesaikannya, menyelesaikan latihan

Itu batas trigonometri Mereka adalah batas fungsi sehingga fungsi -fungsi ini dibentuk oleh fungsi trigonometri.

Ada dua definisi yang harus diketahui memahami bagaimana perhitungan batas trigonometri dilakukan. Definisi ini adalah:

- Batas fungsi "f" ketika "x" cenderung "b": itu terdiri dari menghitung nilai di mana f (x) mendekati sebagai "x" mendekati "b", tanpa menegaskan "b" ".

- Fungsi trigonometri: Fungsi trigonometri adalah fungsi sinus, cosinus dan tangen, yang dilambangkan dengan dosa (x), cos (x) dan tan (x) masing -masing.

Fungsi trigonometri lainnya diperoleh dari tiga fungsi yang disebutkan di atas.

Batas fungsi

Untuk mengklarifikasi konsep batas fungsi, kami akan melanjutkan untuk menunjukkan beberapa contoh dengan fungsi sederhana.

- Batas f (x) = 3 ketika "x" cenderung "8" sama dengan "3", karena fungsinya selalu konstan. Tidak peduli berapa banyak nilainya "X", nilai f (x) akan selalu menjadi "3".

- Batas f (x) = x-2 ketika "x" cenderung "6" adalah "4". Sejak saat "X" dekat dengan "6" lalu "x-2" mendekati "6-2 = 4".

- Batas G (x) = x² ketika "x" cenderung "3" sama dengan 9, karena ketika "x" mendekati "3" lalu "x²" mendekati "3² = 9" ".

Seperti yang dapat dicatat dalam contoh -contoh sebelumnya, menghitung batas terdiri dari mengevaluasi nilai yang “x” cenderung dalam fungsi, dan hasilnya akan menjadi nilai batas, meskipun ini hanya berlaku untuk fungsi berkelanjutan.

Apakah ada batasan yang lebih rumit?

Jawabannya iya. Contoh sebelumnya adalah contoh batas yang paling sederhana. Dalam buku perhitungan, latihan batas utama adalah yang menghasilkan ketidakpastian tipe 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 dan (∞)^0.

Dapat melayani Anda: identitas Pythagoras: demonstrasi, contoh, latihan

Ekspresi ini disebut ketidakpastian karena mereka adalah ekspresi yang secara matematis masuk akal.

Selain itu, tergantung pada fungsi yang terlibat dalam batas asli, hasil yang diperoleh saat menyelesaikan ketidakpastian mungkin berbeda dalam setiap kasus.

Contoh batas trigonometri sederhana

Untuk menyelesaikan batas, selalu sangat berguna untuk mengetahui grafik fungsi yang terlibat. Di bawah ini adalah grafik fungsi sinus, kosinus dan garis singgung.

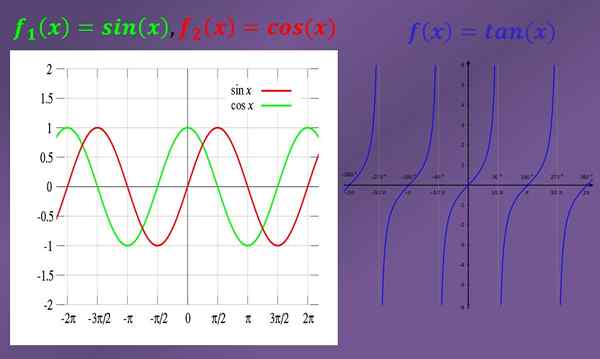
Beberapa contoh batas trigonometri sederhana adalah:

- Hitung batas tanpa (x) saat "x" cenderung "0".

Melihat grafik Anda dapat melihat bahwa jika "x" mendekati "0" (baik di sebelah kiri maupun kanan), maka grafik payudara juga mendekati "0". Oleh karena itu, batas dosa (x) ketika "x" cenderung "0" adalah "0".

- Hitung batas cos (x) ketika "x" cenderung "0".

Mengamati grafik cosinus dapat dilihat bahwa ketika "x" dekat dengan "0" maka grafik kosinus dekat dengan "1". Ini menyiratkan bahwa batas cos (x) ketika "x" cenderung "0" sama dengan "1".

Batas dapat ada (menjadi angka), seperti halnya dalam contoh sebelumnya, tetapi juga dapat terjadi bahwa itu tidak ada seperti yang ditunjukkan dalam contoh berikut.

- Batas tan (x) ketika "x" cenderung "π/2" di sebelah kiri sama dengan "+∞", seperti yang dapat dilihat dalam grafik. Di sisi lain, batas tan (x) ketika "x" cenderung "-π/2" di sebelah kanan sama dengan "-∞".

Identitas Batas Trigonometri

Dua identitas yang sangat berguna ketika batas trigonometri sedang dihitung adalah:

Dapat melayani Anda: pemrograman non -linier: metode dan latihan

- Batas "sin (x)/x" ketika "x" cenderung "0" sama dengan "1".

- Batas "(1-cos (x))/x" ketika "x" cenderung "0" sama dengan "0".

Identitas ini sangat sering digunakan saat Anda memiliki semacam ketidakpastian.

Latihan terpecahkan

Selesaikan batasan berikut menggunakan identitas yang dijelaskan di atas.

- Latihan 1

Hitung batas "f (x) = tanpa (3x)/x" ketika "x" cenderung "0".

Jika fungsi "F" dievaluasi dalam "0" ketidakpastian tipe 0/0 akan diperoleh. Oleh karena itu, kita harus mencoba menyelesaikan ketidakpastian ini dengan menggunakan identitas yang dijelaskan.

Satu -satunya perbedaan antara batas ini dan identitas adalah angka 3 yang muncul dalam fungsi sinus. Untuk menerapkan identitas, fungsi "f (x)" harus ditulis ulang sebagai berikut "3*(tanpa (3x)/3x)". Sekarang, argumen payudara dan penyebutnya sama.

Jadi ketika "X" cenderung "0", menggunakan identitas adalah "3*1 = 3". Oleh karena itu, batas f (x) ketika "x" cenderung "0" sama dengan "3".

- Latihan 2

Hitung batas "g (x) = 1/x - cos (x)/x" ketika "x" cenderung "0".

Ketika "x = 0" diganti dalam g (x) ketidakpastian tipe ∞ -∞. Untuk menyelesaikannya, fraksi dikurangi, yang memberikan sebagai hasilnya "(1-cos (x))/x".

Sekarang, dengan menerapkan identitas trigonometri kedua, batas g (x) adalah bahwa "x" cenderung "0" sama dengan 0.

- Latihan 3

Hitung batas "h (x) = 4tan (5x)/5x" ketika "x" cenderung "0".

Sekali lagi jika h (x) dievaluasi dalam "0" ketidakpastian tipe 0/0 akan diperoleh.

Menulis ulang sebagai (5x) sebagai tanpa (5x)/cos (5x) ternyata h (x) = (tanpa (5x)/5x)*(4/cos (x)))).

Itu dapat melayani Anda: sudut bertuliskan lingkaran: definisi, teorema, contoh

Menggunakan itu batas 4/cos (x) ketika "x" cenderung "0" sama dengan "4/1 = 4" dan identitas trigonometri pertama diperoleh bahwa batas h (x) ketika "x" cenderung "0" sama dengan "1*4 = 4".

Pengamatan

Batas trigonometri tidak selalu mudah dipecahkan. Dalam artikel ini hanya contoh dasar yang ditampilkan.

Referensi

1. Fleming, w., & Varberg, D. DAN. (1989). Matematika Prealculus. Prentice Hall Ptr.
2. Fleming, w., & Varberg, D. DAN. (1989). Matematika Prekalkulus: Pendekatan Pemecahan Masalah (2, ed ilustrasi.). Michigan: Prentice Hall.
3. Fleming, w., & Varberg, D. (1991). Aljabar dan trigonometri dengan geometri analitik. Pendidikan Pearson.
4. Larson, r. (2010). Prealculus (8 ed.). Pembelajaran Cengage.
5. Loyal, J. M., & Viloria, n. G. (2005). Geometri analitik datar. Mérida - Venezuela: Editorial Venezuela C. KE.
6. Pérez, c. D. (2006). Prequalculus. Pendidikan Pearson.
7. Purcell, e. J., VARBERG, D., & Rigdon, s. DAN. (2007). Perhitungan (Edisi kesembilan.). Prentice Hall.
8. Saenz, J. (2005). Perhitungan diferensial dengan fungsi transenden awal untuk sains dan teknik (Edisi kedua Ed.). Sisi miring.
9. Scott, c. KE. (2009). Geometri Pesawat Cartesian, Bagian: Analytical Conics (1907) (Cetak ulang ed.). Sumber petir.
10. Sullivan, m. (1997). Prequalculus. Pendidikan Pearson.