Karakteristik garis tegak lurus, contoh, latihan

A Garis tegak lurus Ini adalah salah satu yang membentuk sudut 90º sehubungan dengan garis, kurva atau permukaan lain. Perhatikan bahwa ketika dua garis tegak lurus dan pada bidang yang sama, saat dipotong mereka membentuk empat sudut yang identik, masing -masing 90º.

Jika salah satu sudut tidak 90º dikatakan bahwa garis itu miring. Garis tegak lurus sering dalam desain, arsitektur dan konstruksi, misalnya jaringan pipa dari gambar berikut.

Gambar 1. Pipa lurus -sudut dan banyak garis tegak lurus. Berapa banyak sudut 90º yang dapat dihitung dalam gambar ini? Sumber: Piqsels.

Orientasi garis tegak lurus dapat beragam, seperti yang ditunjukkan di bawah ini:

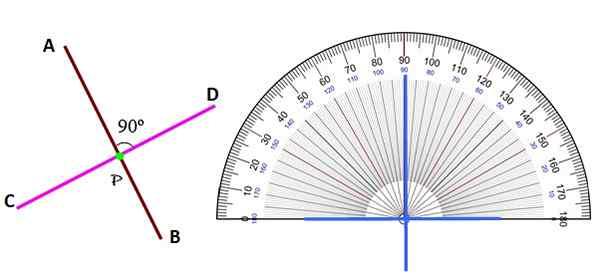
Gambar 2. Garis tegak lurus di pesawat. Sumber: f. Zapata.

Terlepas dari posisinya, garis tegak lurus dikenali dengan mengidentifikasi sudut di antara mereka sebagai 90º, dengan bantuan konveyor.

Perhatikan bahwa tidak seperti garis paralel di pesawat, yang tidak pernah berpotongan, tegak lurus selalu melakukannya pada titik p, yang disebut kaki dari salah satu garis di sisi lain. Oleh karena itu dua garis tegak lurus juga Secantes.

Jalur apa pun yang memiliki tegak lurus yang tak terbatas, karena hanya dengan menggusur segmen AB ke kiri atau kanan pada segmen CD, kami akan memiliki tegak lurus baru dengan kaki lain.

Namun, tegak lurus yang melewati titik tengah segmen disebut bisektris dari segmen tersebut.

[TOC]

Contoh garis tegak lurus

Garis tegak lurus sering di lanskap perkotaan. Dalam gambar berikut (Gambar 3) hanya beberapa dari banyak garis tegak lurus yang dihargai pada fasad sederhana bangunan ini dan unsur -unsurnya seperti pintu, saluran, langkah dan banyak lagi: Lainnya:

Dapat melayani Anda: Fourier Discreet Transformed: Properties, Applications, Contoh Gambar 3. Ada banyak garis tegak lurus di fasad bangunan umum seperti ini. Sumber: Richard Kang melalui Flickr.

Hal yang baik adalah bahwa tiga baris tegak lurus satu sama lain membantu kita menetapkan lokasi titik dan objek di luar angkasa. Adalah sumbu koordinat yang diidentifikasi sebagai Sumbu x, Sumbu y Dan Sumbu z, Terlihat jelas di sudut kamar persegi panjang seperti berikut:

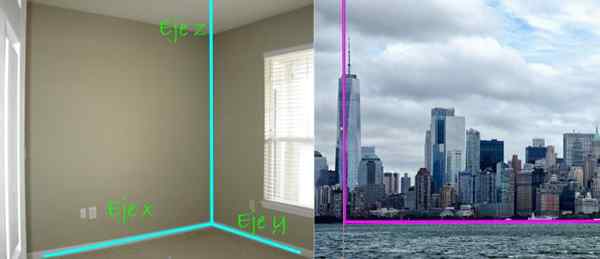Gambar 4. Sistem sumbu cartesian terdiri dari tiga garis tegak lurus satu sama lain, masing -masing memiliki arah preferensial di ruang angkasa. Kredit gambar kiri: Treybunn 2 melalui flickr. Gambar yang benar; Needpix.

Dalam pemandangan kota yang indah, di sebelah kanan, tegak lurus antara gedung pencakar langit dan tanah juga diperingatkan. Yang pertama akan mengatakan bahwa itu ditemukan di seluruh Sumbu z, Sedangkan tanah adalah pesawat, yang dalam hal ini adalah pesawat Xy.

Jika tanah merupakan pesawat Xy, Pencakar langit juga tegak lurus dengan jalan atau jalanan mana pun, yang menjamin stabilitasnya, karena struktur yang cenderung tidak stabil.

Dan di jalanan, di mana pun sudut persegi panjang, ada garis tegak lurus. Banyak jalan dan jalan memiliki tata letak tegak lurus, asalkan tanah dan kecelakaan geografis mengizinkannya.

Untuk secara tiba -tiba mengekspresikan tegak lurus antara garis, segmen atau vektor, simbol ⊥ digunakan. Misalnya, jika garis l₁ tegak lurus terhadap garis l₂, kami menulis:

L₁ ⊥ l₂

Lebih banyak contoh garis tegak lurus

- Dalam desain garis tegak lurus sangat ada, karena banyak objek umum didasarkan pada kotak dan persegi panjang. Quadrilateral ini ditandai dengan memiliki sudut internal 90º, karena sisi mereka dua hingga dua paralel:

Itu dapat melayani Anda: Persamaan Parabola Umum (Contoh dan Latihan)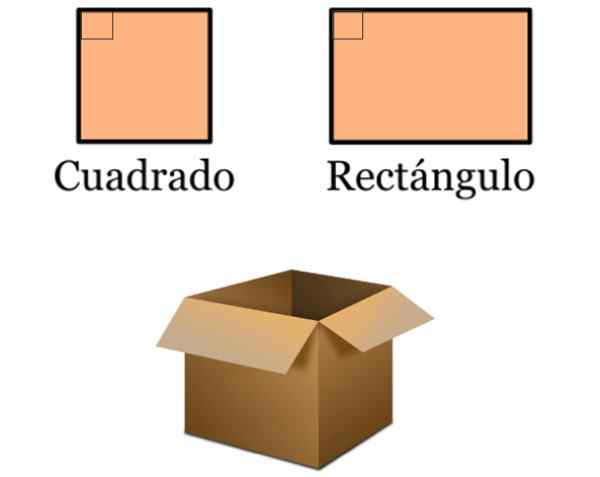 Gambar 5. Kotak dan persegi panjang adalah bagian dari berbagai desain, seperti kotak kardus sederhana ini untuk menyimpan barang dagangan. Sumber: f. Zapata.

- Pengadilan di mana berbagai olahraga dipraktikkan dibatasi oleh banyak kotak dan persegi panjang. Ini pada gilirannya berisi garis tegak lurus.

- Dua segmen yang membentuk segitiga persegi panjang saling tegak lurus. Ini disebut kategori, sedangkan garis yang tersisa dipanggil sisi miring.

- Garis vektor medan listrik tegak lurus terhadap permukaan keseimbangan elektrostatik.

- Untuk pengemudi yang dimuat, peralatan dan peralatan selalu tegak lurus terhadap medan listrik.

- Dalam sistem pipa atau saluran yang digunakan untuk mengangkut berbagai jenis cairan, seperti gas yang muncul pada Gambar 1, adalah umum untuk siku pada sudut kanan. Oleh karena itu mereka membentuk garis tegak lurus, seperti halnya ruang boiler:

Gambar 6. Pipa di ruang boiler. Sumber: Wikimedia Commons. Roger mclassus/cc by-s (http: // createveCommons.Org/lisensi/by-sa/3.0/)

Latihan

- Latihan 1

Gambarlah dua garis tegak lurus dengan aturan dan kompas.

Larutan

Ini sangat mudah dilakukan, mengikuti langkah -langkah ini:

-Baris pertama ditarik, disebut ab (hitam).

-Di atas (atau di bawah jika lebih disukai) dari titik AB Point P, di mana tegak lurus akan lewat. Jika P tepat di atas (atau di bawah) setengah dari AB, tersebut tegak lurus adalah bisektor segmen AB.

-Dengan kompas yang berpusat pada P, sebuah lingkaran ditarik yang memotong AB dalam dua titik, dipanggil ke 'dan b' (merah).

Dapat melayani Anda: nomor ramah atau ramah: contoh dan bagaimana menemukannya

-Kompas dalam a'p dibuka, berfokus pada A 'dan sebuah lingkaran ditarik yang melewati P (hijau).

-Ulangi langkah sebelumnya, tetapi sekarang membuka kompas sepanjang segmen B'p (hijau). Kedua lengkungan keliling dipotong pada titik q di bawah p dan tentu saja di yang terakhir.

-Poin P dan Q bergabung dengan aturan dan garis tegak lurus (biru) sudah siap.

-Akhirnya, semua konstruksi tambahan harus dihapus dengan hati -hati, hanya menyisakan tegak lurus.

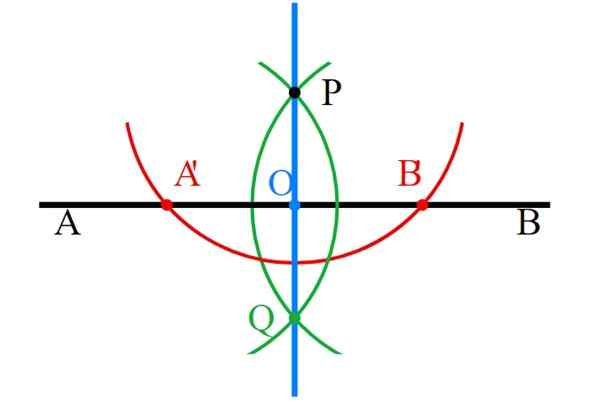Gambar 6. Garis Percendular dengan aturan dan compas. Sumber: Wikimedia Commons.

- Latihan 2

Dua baris l₁ dan saya₂ Mereka tegak lurus jika lerengnya masing -masing m₁ dan m₂ Mereka memenuhi hubungan ini:

M₁ = -1/m₂

Mengingat garis y = 5x - 2, temukan garis tegak lurus padanya dan lewati titik (-1, 3).

Larutan

-Pertama -tama adalah kemiringan garis tegak lurus m_⊥, Seperti yang ditunjukkan dalam pernyataan itu. Kemiringan garis asli adalah M = 5, koefisien yang menyertai "x". Jadi:

M_⊥= -1/5

-Maka persamaan garis tegak lurus dibangun dan_⊥, Mengganti nilai yang sebelumnya ditemukan:

Dan_⊥= -1/5x + b

-Maka nilai B ditentukan, dengan bantuan titik yang diberikan oleh pernyataan, (-1,3), karena garis tegak lurus harus melewatinya:

y = 3

x = -1

Mengganti:

3 = -1/5 (-1) + b

Nilai B dibersihkan:

B = 3- (1/5) = 14/5

-Akhirnya persamaan terakhir dibangun:

Dan_⊥= -1/5x + 14/5

Referensi

1. Baldor, a. 2004. Geometri datar dan ruang. Publikasi Budaya.
2. Clemens, s. 2001. Geometri dengan aplikasi dan pemecahan masalah. Addison Wesley.
3. Matematika itu menyenangkan. Garis tegak lurus. Pulih dari: Mathisfun.com.
4. Institut Monterey. Garis tegak lurus. Pulih dari: montereyinstitute.org.
5. Wikipedia. Garis tegak lurus. Pulih dari: is.Wikipedia.org.