Besarnya vektor

Apa itu magnitudo vektor?

A Besarnya vektor Ini adalah ekspresi apa pun yang diwakili oleh vektor yang memiliki nilai numerik (modul), arah, arah dan titik aplikasi. Beberapa contoh magnitudo vektor adalah perpindahan, kecepatan, kekuatan dan medan listrik.

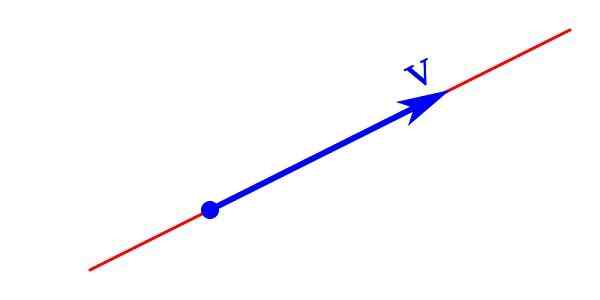
Representasi grafik dari magnitudo vektor terdiri dari panah yang ujungnya menunjukkan arah dan arahnya, panjangnya adalah modul dan titik awal adalah asal atau titik aplikasi.

Representasi grafis vektor

Besarnya vektor diwakili secara analitik dengan surat yang membawa panah di bagian atas menunjuk ke kanan ke arah horizontal. Itu juga dapat diwakili oleh surat yang ditulis dengan huruf tebal V yang modulnya ǀVǀ Ini ditulis dalam huruf miring V.

Salah satu aplikasi konsep besarnya vektor adalah dalam desain jalan raya dan jalan, khususnya dalam desain kelengkungannya. Aplikasi lain adalah perhitungan perpindahan antara dua tempat atau perubahan kecepatan kendaraan.

Elemen dengan besarnya vektor

Besarnya vektor adalah entitas apa pun yang diwakili oleh segmen garis, dengan orientasi dalam ruang, yang memiliki karakteristik vektor. Elemennya adalah:

Modul: Ini adalah nilai numerik yang menunjukkan ukuran atau intensitas besarnya vektor.

Alamat: Ini adalah orientasi segmen garis di ruang yang mengandungnya. Vektor dapat memiliki arah horizontal, vertikal atau miring; Utara, selatan, ini atau barat; Timur laut, tenggara, barat daya atau barat laut.

Nalar: Ditunjukkan dengan ujung panah di ujung vektor.

Itu dapat melayani Anda: Fisika sebelum orang Yunani (Antigua Yunani)

Titik aplikasi: Ini adalah asal atau titik aksi awal vektor.

Klasifikasi Vektor

Vektor diklasifikasikan sebagai collinear, paralel, tegak lurus, bersamaan, bait, gratis, geser, berlawanan, peralatan, tetap dan unit.

Colineal: Mereka milik atau bertindak pada garis lurus yang sama, mereka juga disebut tergantung secara linear Dan mereka bisa vertikal, horizontal dan miring.

Paralel: Mereka memiliki alamat atau kecenderungan yang sama.

Tegak lurus: Dua vektor saling tegak lurus ketika sudut di antara mereka adalah 90 °.

Bersamaan: Mereka adalah vektor yang ketika meluncur di atas garis aksi mereka, mereka bertepatan pada titik yang sama di luar angkasa.

Coplanarios: Mereka bertindak di pesawat, misalnya pesawat Xy.

Bebas: Mereka bergerak di mana saja di ruang menjaga modul, arah, dan makna mereka.

Menggeser: Mereka bergerak di sepanjang garis tindakan yang ditentukan oleh arah mereka.

Lawan: Mereka memiliki modul dan arah yang sama, dan arah yang berlawanan.

Peralatan: Mereka memiliki modul, arah, dan makna yang sama.

Tetap: Titik aplikasi tidak berubah -ubah.

Unitari: Vektor yang modulnya adalah unit.

Komponen vektor

Besarnya vektor dalam ruang tiga dimensi diwakili dalam sistem tiga sumbu tegak lurus satu sama lain (X dan z) disebut ortogonal dicoba.

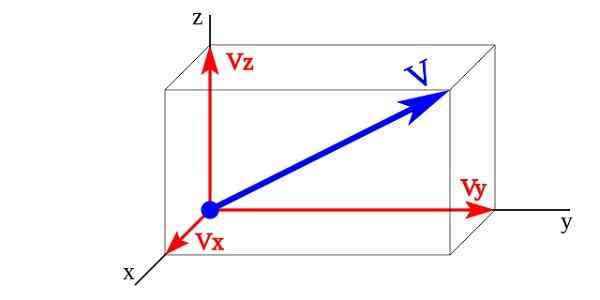Komponen vektor dengan besarnya vektor

Pada gambar vektor Vx, Vy, Vz adalah komponen vektor vektor V vektor unit siapa X,Dan,z. Besarnya vektor V Itu diwakili oleh jumlah komponen vektornya.

V = Vx + Vy + Vz

Hasil dari beberapa magnitudo vektor adalah jumlah vektor dari semua vektor dan menggantikan vektor -vektor ini dalam suatu sistem.

Bidang vektor

Bidang vektor adalah wilayah ruang di mana di masing -masing titiknya magnitudo vektor sesuai. Jika besarnya yang dimanifestasikan adalah kekuatan yang bekerja pada tubuh atau sistem fisik maka medan vektor adalah medan kekuatan.

Dapat melayani Anda: Teorema Steiner: Penjelasan, Aplikasi, Latihan

Bidang vektor diwakili secara grafis oleh garis bidang yang merupakan garis tangen dari magnitudo vektor di semua titik di wilayah tersebut. Beberapa contoh bidang vektor adalah medan listrik yang dibuat oleh muatan listrik tepat waktu di ruang dan kecepatan medan cairan.

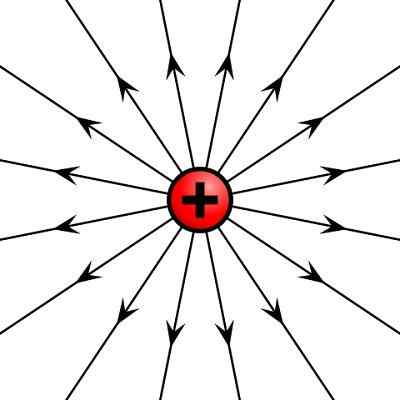Medan listrik yang dibuat oleh muatan listrik yang positif

Operasi dengan vektor

Penambahan vektor: Ini adalah hasil dari dua atau lebih vektor. Jika Anda memiliki dua vektor SALAH SATU Dan P Jumlahnya SALAH SATU + P = q. Vektor Q Itu adalah vektor yang dihasilkan yang diperoleh secara grafis menggerakkan asal vektor KE sampai akhir vektor B.

Pengurangan vektor: Pengurangan dua vektor atau dan P adalah SALAH SATU - P = Q. Vektor Q  Anda menambah vektor SALAH SATU Kebalikannya -P. Metode grafik sama dengan jumlah dengan perbedaan bahwa vektor yang berlawanan ditransfer ke ekstrem.

Produk skalar: Produk dari besarnya skalar ke dengan besarnya vektor P Itu adalah vektor MP yang memiliki arah vektor yang sama P. Jika besarnya skalar nol, produk skalar adalah vektor nol.

Contoh magnitudo vektor

Posisi

Posisi suatu objek atau partikel sehubungan dengan sistem referensi adalah vektor yang diberikan oleh koordinat persegi panjangnya X dan z, dan diwakili oleh komponen vektornya Xî, YJ, ZK. Vektor  yo, J, k Mereka adalah unit vektor.

Sebuah partikel pada satu titik (X dan z) memiliki vektor posisi R = Xî + YJ + ZK. Nilai numerik dari posisi vektor adalah R= √ (X² + Dan² + z²). Perubahan posisi partikel dari satu posisi ke posisi lain sehubungan dengan sistem referensi adalah vektor Perpindahan ΔR Dan dihitung dengan ekspresi vektor berikut:

Dapat melayani Anda: sinar anodik

Δr = r₂ - R₁

Percepatan

Percepatan rata -rata (ke_M) Ini didefinisikan sebagai variasi kecepatan v Dlm suatu waktu Δt Dan ekspresi untuk menghitungnya ke_M= ΔV/Δt, makhluk ΔV Kecepatan perubahan vektor.

Akselerasi instan (ke) adalah batas percepatan rata -rata ke_M Kapan Δt menjadi sangat kecil sehingga cenderung nol. Akselerasi instan dinyatakan sesuai dengan komponen vektornya

ke =ke_Xyo +ke_Dan J+ ke_zk

Medan gravitasi

Gaya tarik gravitasi yang diberikan oleh massa M, Terletak di titik asal, di massa lain M Pada satu titik di luar angkasa X, Dan, z Ini adalah medan vektor yang disebut medan gaya gravitasi. Kekuatan ini diberikan oleh ekspresi:

F= (-mmg/R)ȓ

R = Xî + YJ + ZK

F = Ini adalah gaya gravitasi magnitudo fisik

G = adalah konstanta gravitasi universal

ȓ = adalah vektor posisi massa M

Referensi

1. Tallack, J C. Pengantar Analisis Vektor. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S dan Spellman, D. Vektor analisis. S.l. : MC Graw Hill, 2009.
3. Merek, l. Vektor analisis. New York: Dover Publications, 2006.
4. Griffiths, D J. Pengantar Electodynamics. New Jersey: Prentice Hall, 1999. P. 1-10.
5. Den Haag, b. Pengantar Analisis Vektor. Glasgow: Methuen & Co. Ltd, 2012.