Perhitungan dan olahraga matriks terbalik diselesaikan

Itu Matriks terbalik Dari matriks yang diberikan, itu adalah matriks yang dikalikan dengan hasil asli dalam matriks identitas. Matriks terbalik berguna untuk memecahkan sistem persamaan linier, karenanya pentingnya mengetahui cara menghitungnya.

Matriks sangat berguna dalam fisika, teknik dan matematika, karena mereka adalah alat yang ringkas untuk memecahkan masalah yang kompleks. Kegunaan matriks ditingkatkan ketika mereka dibalik dan juga kebalikannya diketahui.

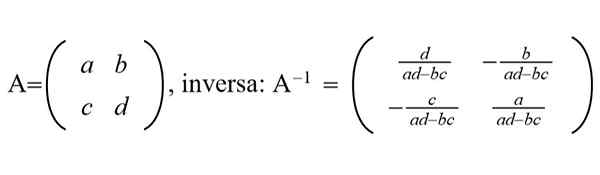Gambar 1. Matriks 2 × 2 generik dan matriks terbalik ditampilkan. (Disiapkan oleh Ricardo Pérez)

Dalam bidang pemrosesan grafis, data besar, penambangan data, pembelajaran mesin dan lainnya digunakan algoritma yang efisien dan cepat untuk mengevaluasi matriks terbalik matriks NXN dengan N yang sangat besar, dalam urutan ribuan atau jutaan orang.

Untuk menggambarkan penggunaan matriks terbalik dalam pengelolaan sistem persamaan linier, kita akan mulai dengan kasus paling sederhana dari semua: 1 × 1 matriks.

Kasus paling sederhana: Persamaan linier dari variabel tunggal dipertimbangkan: 2 x = 10.

Idenya adalah untuk menemukan nilai x, tetapi akan menjadi "matriks". 

Matriks m = (2) yang melipatgandakan vektor (x) adalah matriks 1 × 1 yang menghasilkan vektor (10):

M (x) = (10)

Kebalikan dari matriks M dilambangkan dengan m^-1.

Cara umum menulis "sistem linier" ini adalah:

M x = b, di mana x adalah vektor (x) dan b adalah vektor (10).

Menurut definisi, matriks terbalik adalah tanda yang dikalikan dengan hasil matriks asli dalam matriks identitas I:

M^-1 M = i

Dalam kasus dipertimbangkan, matriks m^-1 Itu adalah matriks (½), yaitu m^-1 = (½) karena m^-1 M = (½) (2) = (1) = i

Dapat melayani Anda: 90 pembagi: Apa itu dan penjelasan

Untuk menemukan vektor x = (x) yang tidak diketahui, dalam persamaan yang ditinggikan, kedua anggota dikalikan dengan matriks terbalik:

M^-1 M (x) = m^-1 (10)

(½) (2) (x) = (½) (10)

(½ 2) (x) = (½ 10)

(1) (x) = (5)

(x) = (5)

Kesetaraan dua vektor telah tercapai, yang hanya sama ketika elemen yang sesuai sama, yaitu x = 5.

Perhitungan kebalikan dari suatu matriks

Yang memotivasi perhitungan matriks terbalik adalah menemukan metode universal untuk solusi sistem linier seperti sistem 2 × 2 berikut:

x - 2 y = 3

-x + y = -2

Mengikuti langkah -langkah kasus 1 × 1, dipelajari di bagian sebelumnya, kami menulis sistem persamaan dengan cara matriks:

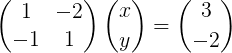Gambar 2. Sistem linier dalam bentuk matriks.

Perhatikan bahwa sistem ini ditulis dalam notasi vektor kompak sebagai berikut:

M x = b

Di mana

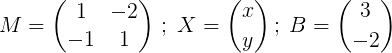
Langkah selanjutnya adalah menemukan m.

Metode 1: Melalui eliminasi Gaussian

Metode eliminasi Gauss akan diterapkan. Yang terdiri dari melakukan operasi dasar pada jajaran matriks, operasi ini adalah:

- Lipat gandakan baris dengan nomor non -null.

- Tambahkan atau kurangi baris lain, atau kelipatan dari baris lain.

- Baris pertukaran.

Tujuannya adalah, melalui operasi ini, untuk mengubah matriks asli menjadi matriks identitas. 

Seperti yang dilakukan, dalam matriks m operasi yang persis sama dengan matriks identitas diterapkan. Ketika setelah beberapa operasi dalam baris R itu diubah menjadi matriks kesatuan, maka yang awalnya kesatuan akan diubah menjadi matriks terbalik dari M, yaitu m, m^-1.

Dapat melayani Anda: akibat wajar (geometri)

1- Kami memulai proses dengan menulis matriks m dan di sebelahnya matriks unit:

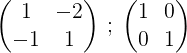
2- Kami menambahkan dua baris dan hasilnya diletakkan di baris kedua, dengan cara ini kami mendapatkan nol di elemen pertama dari baris kedua:

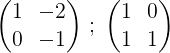
3- Kami mengalikan baris kedua dengan -1 untuk mendapatkan 0 dan 1 di baris kedua:

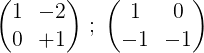
4- Baris pertama dikalikan dengan ½:

5- Yang kedua dan yang pertama menambahkan dan hasilnya ditempatkan di barisan depan:

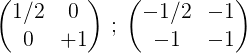
6- Untuk mengakhiri proses, baris pertama dengan 2 dikalikan untuk memperoleh matriks identitas pertama dan pada kedua matriks terbalik dari matriks asli m:

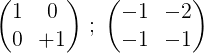
Artinya:

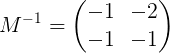
Solusi Sistem

Setelah matriks terbalik diperoleh, sistem persamaan diselesaikan dengan menerapkan matriks terbalik pada kedua anggota persamaan vektor kompak:

M^-1M x = m^-1B

X = m^-1B

Itu secara eksplisit tetap seperti ini:

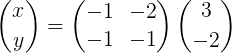
Kemudian perkalian matriks dibuat untuk mendapatkan vektor x:

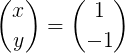
Metode 2: Dengan matriks yang terpasang

Dalam metode kedua ini matriks terbalik dihitung berdasarkan matriks yang terpasang dari matriks asli KE.

Misalkan matriks yang diberikan oleh:

kemana_{aku j} Itu adalah elemen baris yo dan kolom J dari matriks KE.

Lampiran matriks KE Itu akan dipanggil Adj (a) Dan elemen -elemennya adalah:

IKLAN_{aku j} = (-1)^(i+j) ¦ai, j¦

Di mana AI, J Itu adalah matriks minor komplementer yang diperoleh dengan menghilangkan baris I dan kolom j dari matriks asli KE. Batang ¦ ¦ menunjukkan bahwa penentu dihitung, yaitu ¦ai, j¦ Itu adalah penentu matriks minor komplementer.

Dapat melayani Anda: sisi homolog

Formula matriks terbalik

Rumus untuk menemukan matriks terbalik berdasarkan matriks terlampir dari matriks asli adalah sebagai berikut:

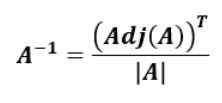
Yaitu matriks terbalik dari KE, KE^-1, adalah transpos dari perlekatan KE dibagi dengan penentu KE.

Yang ditransposkan KE^Tdari sebuah matriks KE Itu adalah yang diperoleh dengan bertukar peringkat untuk kolom, yaitu, baris pertama menjadi kolom pertama dan baris kedua ke kolom kedua dan seterusnya sampai n baris dari matriks asli.

Olahraga diselesaikan

Jadilah matriks ke yang berikutnya:

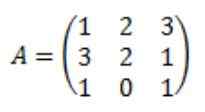
Masing -masing dan setiap elemen dari matriks terpasang dari a: adj (a) dihitung

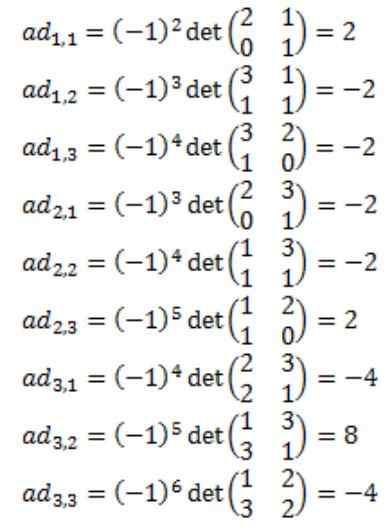
Menghasilkan bahwa matriks terpasang dari A, adj (a) adalah sebagai berikut:

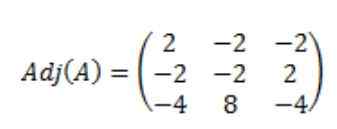
Kemudian penentu matriks A, det (A) dihitung:

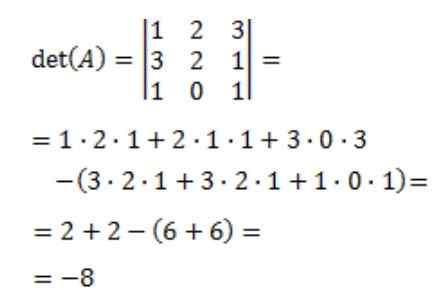
Akhirnya matriks terbalik dari A diperoleh:

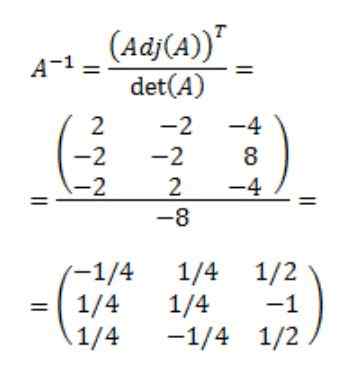
Referensi

1. Anthony Nicolaides (1994) Penentu & Matriks. Lulus publikasi.
2. Awol Assen (2013) Sebuah studi tentang perhitungan penentu 3 × 3
3. Casteleiro Villalba m. (2004) Pengantar aljabar linier. Editorial ESIC.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Matematika: Panduan Kelangsungan Hidup Siswa. Cambridge University Press.
6. Richard J. Brown (2012) 30-detik Matematika: 50 teori yang paling banyak berkembang dalam matematika. Ivy Press Limited.
7. Matriks. Penerbitan Akademik Lap Lambert.