Perkiraan pengukuran contoh dan olahraga figur amorf

Itu Perkiraan pengukuran Dari angka -angka amorf terdiri dari serangkaian metode yang digunakan untuk menentukan area atau perimeter angka geometris yang bukan segitiga, kotak, lingkaran, dll. Beberapa dapat diperpanjang menjadi angka tiga dimensi.

Pada dasarnya pengukuran terdiri dari membuat reticulate secara teratur, seperti persegi panjang, kotak atau trapesium, yang menutupi sekitar permukaan. Keakuratan pendekatan area yang diperoleh dengan metode ini meningkat dengan kemahiran atau kepadatan reticulate.

Gambar 1. Batu berbentuk seperti sosok amorf. Sumber: PXFUEL.

Gambar 1 dan 2 menunjukkan berbagai figur amorf. Untuk menghitung area tersebut, reticulate, terdiri dari kotak 2 x 2, yang pada gilirannya dibagi menjadi dua puluh lima kotak 2/5 x 2/5.

Menambahkan area kuadrat utama dan kotak sekunder. Area perkiraan sosok amorf diperoleh.

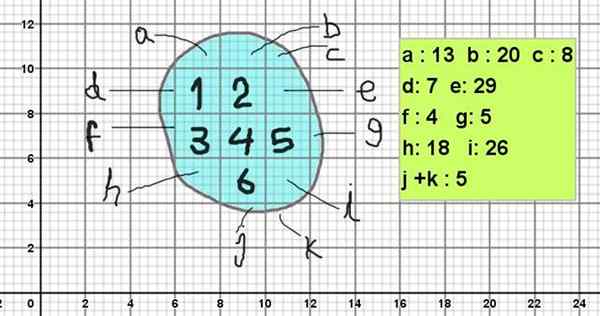
Gambar 2. Reticulate untuk menghitung luas salah satu figur amorf dengan cara perkiraan. Sumber: f. Zapata

[TOC]

Area di bawah kurva

Sering diperlukan untuk menghitung area di bawah kurva antara dua nilai batas. Dalam hal ini, alih -alih reticulate persegi, garis -garis persegi panjang dapat ditelusuri sekitar area di bawah kurva tersebut.

Jumlah semua garis persegi panjang disebut Jumlah atau jumlah Riemann. Gambar 3 menunjukkan partisi interval [a, b] di mana Anda ingin menentukan kira -kira area di bawah kurva.

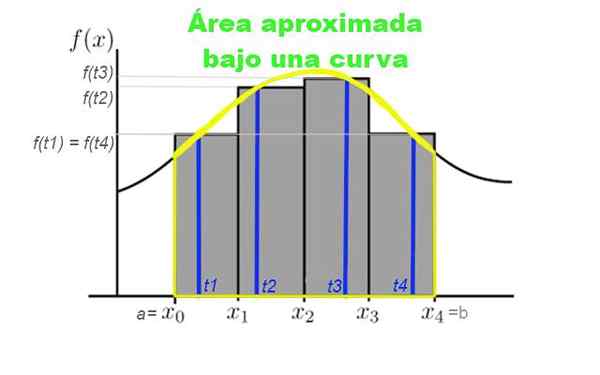Gambar 3. Partisi interval [a, b] dalam empat subinterval, yang biasanya diambil dari lebar yang sama. Ketinggian persegi panjang ditentukan oleh nilai kurva untuk TK milik subinterval. Sumber: f. Zapata.

Misalkan Anda ingin menghitung area di bawah kurva yang diberikan oleh fungsi y = f (x), di mana x milik interval [a, b] di mana Anda ingin menghitung area tersebut. Untuk ini, partisi elemen N dalam interval ini dibuat:

Dapat melayani Anda: 60 pembagi

Partisi = x0 = a, x1, x2, ..., xn = b.

Kemudian perkiraan area di bawah kurva yang diberikan oleh y = f (x) dalam interval [a, b] dicapai dengan jumlah berikut:

S = ∑_{K = 1}^N f (t_k) (X_k - X_K-1)

Dimana t_k adalah antara x_K-1 dan x_k: X_K-1 ≤ t_k ≤ x_k .

Gambar 3 menunjukkan jumlah riemann dari kurva y = f (x) dalam interval [x0, x4]. Dalam hal ini, partisi dari empat subinterval dibuat dan jumlahnya mewakili luas total persegi panjang abu -abu. 

Jumlah ini mewakili pendekatan ke area di bawah kurva F antara absssis x = x0 dan x = x4.

Pendekatan ke area di bawah kurva meningkat sejauh angka N partisi lebih besar, dan cenderung menjadi area di bawah kurva saat angka N Partisi cenderung tak terbatas. 

Dalam hal kurva diwakili oleh fungsi analitik, nilai f (t_k) Mereka dihitung mengevaluasi fungsi tersebut dalam nilai t_k. Tetapi jika kurva tidak memiliki ekspresi analitik, maka kemungkinan berikut tetap:

1. Mendekati kurva dengan fungsi, misalnya polinomial.
2. Ambil koordinat cartesian dari titik di mana kurva dicegat dengan garis x = t_k.

Berkala

Tergantung pada pilihan nilai TK dalam interval [x_k, X_K-1], jumlah tersebut dapat melebih -lebihkan atau meremehkan nilai pasti area di bawah kurva fungsi y = f (x). Hal yang paling disarankan adalah mengambil titik TK di mana area yang hilang kira -kira sama dengan area yang tersisa, meskipun tidak selalu mungkin untuk membuat pilihan seperti itu.  

Dapat melayani Anda: invers multiplikasi: penjelasan, contoh, latihan terpecahkan

Ambil TK di akhir

Hal yang paling praktis adalah menggunakan interval reguler Δx = (b - a)/n, di mana a dan b adalah nilai minimum dan maksimum absis, sedangkan n adalah jumlah subdivisi.

Dalam hal ini, area di bawah kurva mendekat dengan:

Area = f (a+Δx)+f (a+2Δx)+...+f [a+(n-1] Δx+f (b)*Δx

Dalam ungkapan sebelumnya, TK diambil di ujung kanan subinterval.

Ambil TK di ujung kiri

Kemungkinan praktis lainnya adalah mengambil nilai TK di ujung kiri, dalam hal ini jumlah yang mendekati area dinyatakan sebagai:

Area = [f (a)+f (a+Δx)+...+f (a+(n-1) Δx)*Δx

Tk sebagai nilai pusat

Dalam kasus Tk dipilih sebagai nilai sentral dari subinterval reguler dari lebar Δx, jumlah yang mendekati area di bawah kurva adalah:

Area = [f (a+Δx/2)+f (a+3Δx/2)+...+f (b- Δx/2)]*Δx

Ekspresi ini cenderung ke nilai yang tepat sejauh jumlah subdivisi secara sewenang -wenang, yaitu Δx cenderung nol, tetapi dalam hal ini jumlah syarat dari jumlah tersebut sangat besar dengan konsekuensi biaya komputasi konsekuensi komputasi konsekuensi komputasi yang konsekuensinya. 

Contoh

Gambar 2 menunjukkan sosok amorf, yang konturnya mirip dengan batu gambar 1. Untuk menghitung luasnya, ditempatkan pada reticulate dengan kotak utama 2 x 2 unit ke kotak (misalnya mereka bisa 2 cm²).

Dan karena setiap kuadrat dibagi lagi menjadi subdivisi 5 x 5, maka setiap subdivisi memiliki luas 0,4 x 0,4 unit persegi (0,16 cm²).

Gambar dalam gambar akan dihitung sebagai berikut:

Dapat melayani Anda: faktorisasi umum: contoh dan latihan

Area = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

Artinya:

Area = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Olahraga diselesaikan

Hitung kira -kira area di bawah kurva yang diberikan oleh fungsi f (x) = x² Bertaruh a = -2 hingga b = +2. Untuk melakukan ini, tulis jumlah untuk n partisi reguler interval [a, b] dan kemudian ambil batas matematika untuk kasus bahwa jumlah partisi cenderung tak terbatas. 

Larutan

Pertama, interval partisi didefinisikan sebagai 

Δx = (b - a)/n. 

Maka jumlah untuk hak yang sesuai dengan fungsi f (x) adalah seperti ini:

A = -2 dan b =+2 diganti sehingga interval atau langkah adalah Δx = 4/n. Dalam hal ini jumlah untuk fungsi f (x) = x² adalah:

 Binomial persegi dikembangkan: 

[-2 +(4i/n)]² = 4 - 16 I /N + (4 /n)² yo²

Dan kemudian diganti dalam jumlah:

Memisahkan penjumlahan dan mengambil jumlah konstan sebagai faktor umum dari setiap jumlah diperoleh:

 Yang pertama dari jumlah, yang kedua adalah:

Dan yang ketiga adalah:

Mengganti ekspresi jumlah yang Anda miliki:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Saat memilih nilai besar untuk n Anda memiliki pendekatan yang baik untuk area di bawah kurva. Namun, dalam hal ini dimungkinkan untuk mencapai nilai yang tepat dengan mengambil batas matematika ketika n cenderung tak terbatas:

Area = Lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²]

Area = 16 - (64/2)+ (64/3) = 16/3 = 5.333.

Referensi

1. Casteleiro, J. M. 2002. Perhitungan Komprehensif (Edisi Ilustrasi). Madrid: editorial ESIC.
2. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
3. Purcell, e. 2007. Perhitungan dengan geometri analitik. 9NA. Edisi. Pendidikan Pearson.
4. Unican. Sejarah konsep integral. Pulih dari: repositori.Unican.adalah
5. Uis. Jumlah Riemann. Pulih dari: matematika.Uis.Edu.bersama
6. Wikipedia. Daerah. Pulih dari: is.Wikipedia.com