Karakteristik Gerakan Burkasial Seragam, Formula, Latihan

Dia Gerakan Garis Seragam atau dengan kecepatan konstan adalah di mana partikel bergerak di sepanjang garis lurus dan dengan kecepatan konstan. Dengan cara ini ponsel menempuh jarak yang sama di waktu yang sama. Misalnya, jika dalam 1 detik itu berjalan 2 meter, setelah 2 detik akan ada 4 meter dan seterusnya.

Untuk membuat deskripsi yang akurat tentang gerakan ini, baik seragam bujursangkar atau lainnya, perlu untuk menetapkan titik referensi, juga disebut asal, Mengenai posisi perubahan seluler.

Gambar 1. Sebuah mobil yang bergerak di sepanjang jalan bujursangkar dengan kecepatan konstan memiliki gerakan bujursangkar yang seragam. Sumber: Pixabay.

Jika gerakan berlalu sepenuhnya di sepanjang garis lurus, itu juga tertarik untuk mengetahui dalam arti apa perjalanan ponsel.

Pada garis horizontal, ada kemungkinan bahwa ponsel menuju ke kanan atau ke kiri. Perbedaan antara dua situasi dibuat oleh tanda-tanda, berikut ini sebagai berikut: Di sebelah kanan saya ikuti (+) dan ke tanda kiri (-).

Ketika kecepatan konstan, ponsel tidak mengubah arah atau maknanya, dan juga besarnya kecepatannya tetap tidak berubah.

[TOC]

Karakteristik

Karakteristik utama dari gerakan bubur seragam (MRU) adalah sebagai berikut:

-Gerakan selalu melewati garis lurus.

-Ponsel dengan MRU menempuh jarak atau spasi yang sama di waktu yang sama.

-Kecepatan tetap tidak dapat diubah baik dalam besarnya dan arah.

-MRU tidak memiliki akselerasi (tidak ada perubahan kecepatan).

-Sejak kecepatan v tetap konstan dari waktu ke waktu T, Grafik besarnya sebagai fungsi waktu adalah garis lurus. Dalam contoh Gambar 2, garis berwarna hijau dan nilai kecepatan dibaca pada sumbu vertikal, sekitar +0.68 m/s.

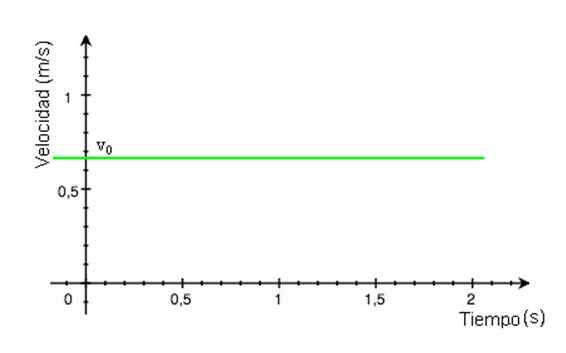Gambar 2. Grafik kecepatan tergantung pada mru. Sumber: Wikimedia Commons.

-Grafik posisi x sehubungan dengan waktu adalah garis lurus, yang kemiringannya setara dengan kecepatan seluler. Jika garis grafik x vs t horizontal, ponsel sedang istirahat, jika kemiringannya positif (grafik Gambar 3), kecepatannya juga.

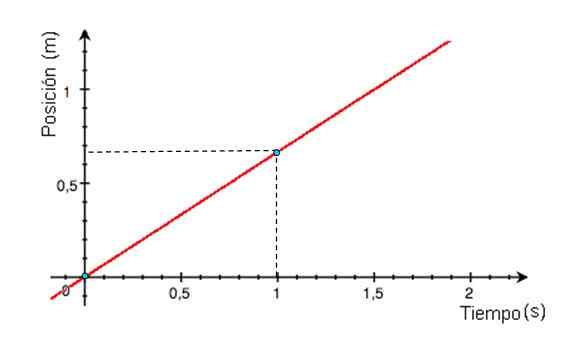Gambar 3. Grafik posisi sebagai fungsi waktu untuk ponsel dengan MRU yang berangkat dari asal. Sumber: Wikimedia Commons.

Jarak yang ditempuh dari grafik v vs. T

Ketahui jarak yang ditempuh oleh ponsel saat grafik tersedia V Vs. t sangat sederhana. Jarak yang ditempuh setara dengan area di bawah garis dan termasuk dalam interval waktu yang diinginkan.

Itu dapat melayani Anda: percepatan rata -rata: bagaimana itu dihitung dan dipecahkan

Misalkan Anda ingin tahu jarak yang ditempuh oleh ponsel dari Gambar 2 dalam interval antara 0.5 dan 1.5 detik.

Area ini adalah persegi panjang yang teduh pada Gambar 4. Itu dihitung dengan menemukan hasil dari mengalikan dasar persegi panjang dengan tinggi badannya, yang nilainya dibaca dari grafik.

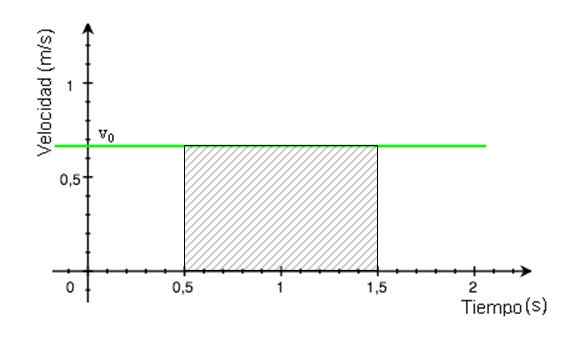Gambar 4. Area bergaris setara dengan jarak yang ditempuh. Sumber: Modifikasi Wikimedia Commons.

Jarak ditempuh = (1.lima puluh.5) x 0.68 m = 0.68 m

Jarak selalu jumlah positif, terlepas dari apakah Anda pergi ke kanan atau ke kiri.

Rumus dan Persamaan

Dalam MRU, kecepatan rata -rata dan kecepatan sesaat selalu sama dan karena nilainya adalah kemiringan grafik x vs t yang sesuai dengan garis, persamaan yang sesuai tergantung pada waktu adalah sebagai berikut:

-Posisi tergantung waktu: x (t) = x_{salah satu} + Vt

X_{salah satu} Itu mewakili posisi awal ponsel, pada banyak kesempatan itu bertepatan dengan asal sistem referensi, tetapi tidak selalu seperti ini. Persamaan ini juga dikenal sebagai Persamaan rencana perjalanan.

-Kecepatan tergantung waktu: v (t) = konstan

Saat V = 0 berarti ponsel itu istirahat. Istirahat adalah kasus gerakan tertentu.

-Akselerasi sebagai fungsi waktu: A (t) = 0

Dalam gerakan bubur seragam yang seragam tidak ada perubahan kecepatan, oleh karena itu akselerasinya nol.

Latihan terpecahkan

Pada saat menyelesaikan latihan, harus dipastikan bahwa situasinya sesuai dengan model yang akan digunakan. Khusus sebelum menggunakan persamaan MRU, perlu untuk memastikan bahwa mereka berlaku.

Latihan berikut yang diselesaikan adalah dua masalah seluler.

Latihan diselesaikan 1

Dua atlet saling mendekati dengan kecepatan konstan 4.50 m/s dan 3.5 m/s masing -masing, awalnya dipisahkan jarak 100 meter, seperti yang ditunjukkan pada gambar.

Jika masing -masing mempertahankan kecepatan konstannya, temukan: a) Berapa lama waktu yang dibutuhkan untuk bertemu? b) Apa yang akan menjadi posisi masing -masing pada waktu itu?

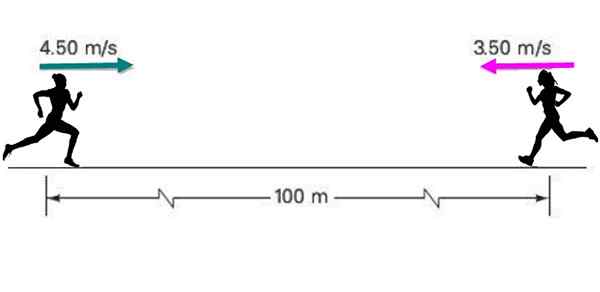Gambar 5. Dua pelari bergerak satu sama lain konstan. Sumber: Made sendiri.

Larutan

Yang pertama adalah menunjukkan asal usul sistem koordinat yang akan berfungsi sebagai referensi. Pilihannya tergantung pada preferensi yang dimiliki orang yang memecahkan masalah.

Dapat melayani Anda: apa itu pelebaran volumetrik? (Dengan contoh)

Biasanya dipilih x = 0 tepat di titik awal ponsel, itu bisa menjadi pelari kiri atau kanan, bahkan dapat dipilih di tengah keduanya.

a) Kami akan memilih x = 0 pada pelari kiri atau runner 1, oleh karena itu posisi awal dari ini adalah x₀₁ = 0 dan untuk runner 2 akan menjadi x₀₂ = 100 m. Pialang 1 Bergerak dari kiri ke kanan dengan kecepatan v₁ = 4.50 m/ sementara Runner 2 melakukannya dari kanan ke kiri dengan kecepatan -3.50 m/s.

Persamaan gerakan untuk broker pertama

X₁ = x₀₁ + v₁T₁ = 4.50t₁

Persamaan Gerakan untuk Pialang Kedua

X₂ = x₀₂ + v₂T₂ = 100 -3.50t₂

Karena waktu sama untuk keduanya T₁ = t₂ = t , Ketika posisi keduanya akan sama, karenanya X₁ = x₂. Setara:

4.50T = 100 -3.50t

Ini adalah persamaan tingkat pertama untuk waktu, yang solusinya t = 12.5 s.

b) Kedua pelari berada di posisi yang sama, oleh karena itu mengganti waktu yang diperoleh di bagian sebelumnya di salah satu persamaan posisi. Misalnya kita dapat menggunakan Runner 1:

X₁ = 4.50t₁ = 56.25 m

Hasil yang sama diperoleh dengan mengganti t = 12.5 detik di Posisi Runner Persamaan 2.

-Latihan diselesaikan 2

Kelinci menantang kura -kura untuk menempuh jarak 2.4 km dan agar adil menawarkan setengah jam keuntungan. Dalam permainan, The Turtle maju dengan alasan 0.25 m/s, yang merupakan maksimum yang dapat berjalan. Setelah 30 menit kelinci berjalan pada 2 m/s dan mencapai kura -kura dengan cepat.

Setelah melanjutkan selama 15 menit lagi, pikir dia punya waktu untuk tidur siang dan masih memenangkan perlombaan, tetapi tertidur selama 111 menit. Ketika dia bangun, dia berlari dengan sekuat tenaga, tetapi kura -kura sudah melintasi gawang. Menemukan:

a) Keuntungan apa yang dimenangkan kura -kura?

b) momen waktu di mana kelinci memajukan kura -kura

c) momen di mana kura -kura maju ke kelinci.

Solusi untuk)

Perlombaan dimulai t = 0. Posisi kura -kura: X_T = 0.25t

Gerakan kelinci memiliki bagian -bagian berikut:

Dapat melayani Anda: Sistem Surya: Planet, Karakteristik, Asal, Evolusi

-Istirahat untuk keuntungan yang diberikannya kepada kura -kura: 0 < t < 30 minutos:

-Berlomba untuk mencapai kura -kura dan terus berlari sedikit setelah melewatinya; Secara total mereka adalah 15 menit gerakan.

-Tidur selama 111 menit (istirahat)

-Bangun terlambat (sprint terakhir)

2.4 km = 2400 m

Durasi lomba adalah: T = 2400 m/ 0.25 m/s = 9600 s = 160 menit. Saat ini kami mengurangi 111 menit dari NAP dan 30 keunggulan, yaitu 19 menit (1140 detik). Itu berarti dia berlari selama 15 menit sebelum tidur dan 4 menit setelah bangun untuk sprint.

Pada saat ini kelinci menutupi jarak berikut:

D_L = 2 m/s . (limabelas . 60 detik) + 2 m/s (4. 60 s) = 1800 m + 480 m = 2280 m.

Karena total jarak adalah 2400 meter, mengurangi kedua nilai, ternyata kelinci tidak memiliki 120 meter untuk mencapai tujuan.

Solusi b)

Posisi kelinci sebelum tertidur X_L = 2 (t - 1800), Mempertimbangkan penundaan 30 -menit = 1800 detik. Sama dengan x_T dan x_L Kami menemukan waktu mereka:

2 (t - 1800) = 0.25t

2t -0.25 t = 3600

T = 2057.14 s = 34.29 menit

Solusi C)

Pada saat kelinci itu diajukan oleh kura -kura, yang tertidur di 1800 meter dari permainan:

1800 = 0.25t

T = 7200 s = 120 menit

Aplikasi

MRU adalah gerakan paling sederhana yang dapat dibayangkan dan itulah sebabnya ini adalah yang pertama dipelajari dalam sinematik, tetapi banyak gerakan kompleks dapat digambarkan sebagai kombinasi dari ini dan gerakan sederhana lainnya.

Jika seseorang meninggalkan rumahnya dan mengarah sampai dia mencapai jalan raya longsor panjang yang melaluinya ia melakukan perjalanan dengan kecepatan yang sama untuk waktu yang lama, gerakannya sebagai MRU dapat dijelaskan, tanpa membahas lebih rinci.

Tentu saja orang tersebut perlu mengambil beberapa putaran sebelum memasuki dan meninggalkan jalan raya, tetapi melalui penggunaan model gerakan ini, durasi perjalanan dapat diperkirakan mengetahui jarak perkiraan antara titik awal dan titik kedatangan.

Di alam, cahaya memiliki gerakan bujursangkar yang seragam yang kecepatannya 300.000 km/s. Juga pergerakan suara di udara dapat diasumsikan seragam bujursangkar dengan kecepatan 340 m/s di berbagai aplikasi.

Saat menganalisis masalah lain, misalnya pergerakan pembawa beban di dalam kawat konduktif, pendekatan MRU juga dapat digunakan untuk memberikan gambaran tentang apa yang terjadi di dalam pengemudi.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.40-45.
2. Figueroa, d. Seri Fisik untuk Sains dan Teknik. Volume 3. Edisi. Kinematika. 69-85.
3. Giancoli, d.  Fisika: Prinsip dengan aplikasi. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Ilmu Fisik Konseptual. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, l. 2007. Fisika: Pandangan Dunia. 6^ta Edisi Singkat. Pembelajaran Cengage. 15-19.
6. Wilson, J. 2011. Fisika 10. Pendidikan Pearson. 116-119.