Metode Euler untuk apa penggunaan prosedur dan latihan

Dia Metode Euler Ini adalah prosedur paling mendasar dan sederhana yang digunakan untuk menemukan perkiraan solusi numerik, untuk persamaan diferensial biasa dari urutan pertama, asalkan kondisi awalnya diketahui.

Persamaan diferensial biasa (EDO) adalah persamaan yang menghubungkan fungsi yang tidak diketahui dari variabel independen tunggal dengan turunannya.

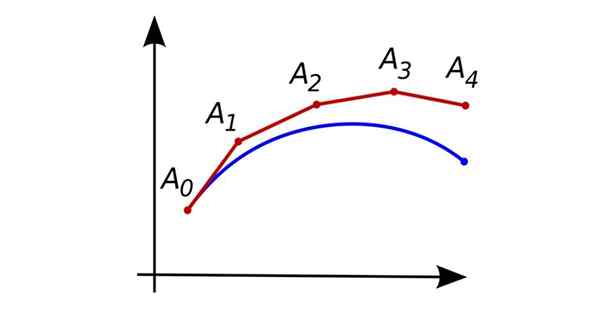
Pendekatan berturut -turut dengan metode Euler. Sumber: Oleg Alexandrov [Domain Publik]

Jika turunan terbesar yang muncul dalam persamaan adalah derajat satu, maka itu adalah persamaan diferensial biasa dari tingkat pertama.

Cara paling umum untuk menulis persamaan tingkat pertama adalah:

dengan kondisi awal:

x = x₀

y = y₀

[TOC]

Apa metode Euler?

Gagasan metode Euler adalah menemukan solusi numerik untuk persamaan diferensial dalam interval antara x₀ dan x_F .

Pertama, interval dalam poin N+1 tidak setuju:

X₀, X₁, X₂, X₃…, X_N

Yang diperoleh seperti ini:
X_yo= x₀+AKU H

Di mana h adalah lebar atau langkah subinterval:

Semakin besar angka dan hasilnya akan lebih tepat, tetapi lebih banyak poin akan diperlukan untuk mencakup interval di mana kita mencari solusinya dan waktu komputasi tumbuh.

Dengan kondisi awal, maka dimungkinkan juga untuk mengetahui turunannya di awal:

dan '(x_{salah satu}) = f (x_{salah satu}, Dan_{salah satu})

Turunan ini mewakili kemiringan garis garis singgung ke kurva fungsi y (x) secara tepat pada titik:

Ao = (x_{salah satu}, Dan_{salah satu})

Kemudian perkiraan prediksi nilai fungsi y (x) dibuat pada titik berikut:

dan (x₁) ≈ dan₁

Dan_1 = Dan_{salah satu} +(X₁- X_{salah satu}) f (x_{salah satu}, Dan_{salah satu}) = y_{salah satu +} H f (x_{salah satu}, Dan_{salah satu})

Titik perkiraan berikutnya dari solusi yang sesuai dengan:

KE₁ = (x₁, Dan₁)

Prosedur ini diulang untuk mendapatkan poin berturut -turut

Dapat melayani Anda: Fungsi Logaritmik: Properti, Contoh, Latihan

KE₂, KE₃…, X_N

Pada gambar yang ditunjukkan pada awalnya, kurva biru mewakili solusi yang tepat dari persamaan diferensial, dan yang merah mewakili titik perkiraan berturut -turut yang diperoleh dengan prosedur Euler.

Latihan terpecahkan

Latihan 1

yo) Menjadi persamaan diferensial:

Dengan kondisi awal x = a = 0; Dan_ke= 1

Dengan menggunakan metode Euler, dapatkan solusi perkiraan Dan Dalam koordinat x = b = 0.5, membagi interval [a, b] pada n = 5 bagian.

Larutan

Hasil numerik dirangkum sebagai berikut:

Di mana disimpulkan bahwa solusi dan untuk nilai 0.5 adalah 1.4851.

Catatan: Untuk realisasi perhitungan yang telah digunakan Studio Smath, Program Penggunaan Gratis Gratis.

Latihan 2

Ii) Melanjutkan dengan persamaan diferensial Latihan i), temukan solusi yang tepat dan bandingkan dengan hasil yang diperoleh dengan metode Euler. Temukan kesalahan atau perbedaan antara hasil yang tepat dan perkiraan.

Larutan

Dengan kondisi awal x = a = 0; Dan_ke= 1
Solusi yang tepat tidak terlalu sulit ditemukan. Diketahui bahwa turunan dari fungsi sen (x) adalah fungsi cos (x). Oleh karena itu solusi y (x) adalah:

dan (x) = sin x + c

Untuk memenuhi kondisi awal dan (0) = 1, konstanta C harus bernilai 1. Selanjutnya, hasil yang tepat dibandingkan dengan perkiraan:

Disimpulkan bahwa dalam interval yang dihitung, pendekatan ini memiliki tiga angka akurasi yang signifikan.

Latihan 3

AKU AKU AKU) Pertimbangkan persamaan diferensial dan kondisi awal yang diberikan di bawah ini:

dan '(x) =- y²

Dengan kondisi awal x₀ = 0; Dan₀ = 1

Gunakan metode Euler untuk menemukan nilai perkiraan solusi dan (x) Dalam interval x = [0, 1.5]. Gunakan langkah H = 0.1.

Larutan

Metode Euler sangat diindikasikan untuk digunakan dengan spreadsheet. Dalam hal ini kami akan menggunakan spreadsheet Geogebra, Program penggunaan gratis dan gratis.

Itu dapat melayani Anda: proporsionalitas majemuk: penjelasan, tiga aturan majemuk, latihan

Tiga kolom (A, B, C) ditampilkan dalam spreadsheet gambar X , Kolom kedua mewakili variabel Dan, dan kolom ketiga turunannya Dan'.

Baris 2 berisi nilai awal X, DAN, DAN' .

Nilai nilai 0.1 Telah ditempatkan di sel posisi absolut ($ D $ 4).

Nilai Y0 awal adalah dalam sel B2, dan Y1 di sel B3. Untuk menghitung dan₁ Formulanya digunakan:

Dan_1 = Dan_{salah satu} +(X₁- X_{salah satu}) f (x_{salah satu}, Dan_{salah satu}) = y_{salah satu +} H f (x_{salah satu}, Dan_{salah satu})

Formula spreadsheet ini akan menjadi b3: = b2 + $ d $ 4 * C3.

Demikian pula Y2 akan berada di sel B4 dan rumusnya ditunjukkan pada gambar berikut:

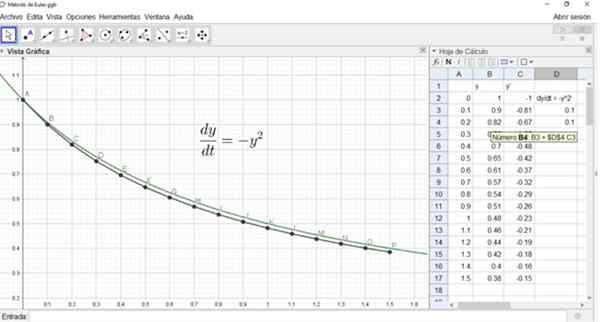
Gambar ini juga menunjukkan grafik dari solusi yang tepat, dan titik A, B, ..., p dari solusi perkiraan dengan menggunakan metode Euler.

Metode Newton Dynamics dan Euler

Dinamika klasik dikembangkan oleh Isaac Newton (1643 - 1727). Motivasi asli Leonard Euler (1707 - 1783) untuk mengembangkan metodenya justru menyelesaikan persamaan hukum kedua Newton dalam berbagai situasi fisik.

Hukum kedua Newton sering dinyatakan sebagai persamaan diferensial sekunder:

Di mana X mewakili posisi objek saat ini T. Objek ini memiliki massa M dan mengalami kekuatan F. Fungsinya F Ini terkait dengan kekuatan dan massa sebagai berikut:

 Meskipun metode Euler pada prinsipnya dirancang untuk memecahkan persamaan diferensial -legree pertama, itu mudah diperluas ke kasus -degree kedua, karena setara dengan sistem dua persamaan derajat pertama pertama.

Itu dapat melayani Anda: geometri analitik

Untuk menerapkan metode Euler, nilai waktu awal diperlukan T, kecepatan v dan posisi X.

Tabel berikut menjelaskan bagaimana mulai dari nilai awal T1, V1, x1 Perkiraan kecepatan V2 dan posisi x2 dapat diperoleh, pada saat T2 = T1+Δt, di mana Δt mewakili peningkatan kecil dan sesuai dengan langkah tersebut dalam metode Euler.

Latihan 4

Iv) Salah satu masalah mendasar dalam mekanika adalah blok massa yang terikat pada pegas (atau pegas) dari konstanta elastis k.

Hukum kedua Newton untuk masalah ini akan seperti ini:

Dalam contoh ini, untuk menyederhanakannya akan diambil m = 1 dan k = 1. Temukan perkiraan solusi untuk posisi tersebut X Dan kecepatannya v Dengan metode Euler dalam interval waktu [0, π/2] membagi interval dalam 12 bagian.

Ambil 0 sebagai momen awal, kecepatan awal 0 dan posisi awal 1.

Larutan

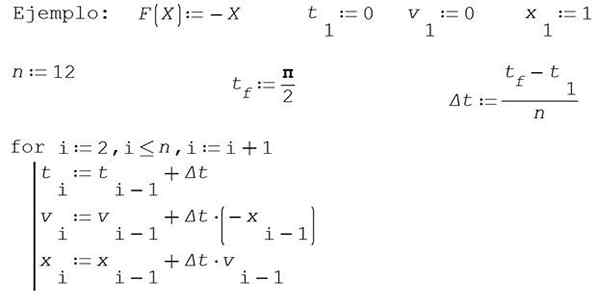
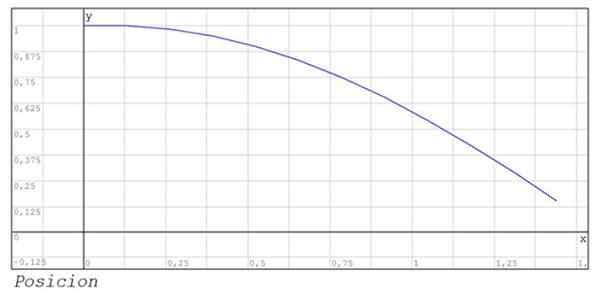
Hasil numerik ditunjukkan pada tabel berikut:

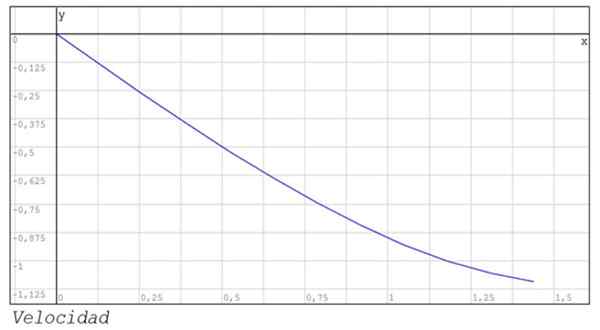
Grafik posisi dan kecepatan antara instan 0 dan 1 juga ditampilkan.44.

Latihan yang diusulkan untuk rumah

Latihan 1

Gunakan spreadsheet untuk menentukan solusi perkiraan menggunakan metode Euler untuk persamaan diferensial:

dan '= -exp (-y) dengan kondisi awal x = 0, y = -1 dalam interval x = [0, 1]

Mulailah dengan langkah 0,1. Grafik hasilnya.

Latihan 2

Dengan menggunakan spreadsheet, temukan solusi numerik untuk persamaan tingkat kedua berikut, di mana dan itu merupakan fungsi dari variabel independen t.

dan "= - 1/y² dengan kondisi awal t = 0; y (0) = 0,5; dan '(0) = 0

Temukan solusi dalam interval [0,5; 1.0] menggunakan langkah 0,05.

Grafik hasilnya: dan vs t; dan 'vs t

Referensi

1. Metode Eurler.Diambil dari Wikipedia.org
2. Euler Solver. Diambil dari.Smath.com