Penjelasan metode Gauss-Seidel, aplikasi, contoh
- 4350
- 333
- Mr. Darrell Streich
Dia Metode Gauss-Seidel Ini adalah prosedur berulang untuk menemukan solusi perkiraan untuk sistem persamaan aljabar linier dengan presisi yang dipilih secara sewenang -wenang. Metode ini berlaku untuk matriks persegi dengan elemen non -non -non -diagonal dan konvergensi dijamin jika matriks dominan secara diagonal.
Itu diciptakan oleh Carl Friedrich Gauss (1777-1855), yang membuat demonstrasi pribadi kepada salah satu muridnya pada tahun 1823. Selanjutnya secara resmi diterbitkan oleh Philipp Ludwig von Seidel (1821-1896) pada tahun 1874, karenanya nama kedua ahli matematika.
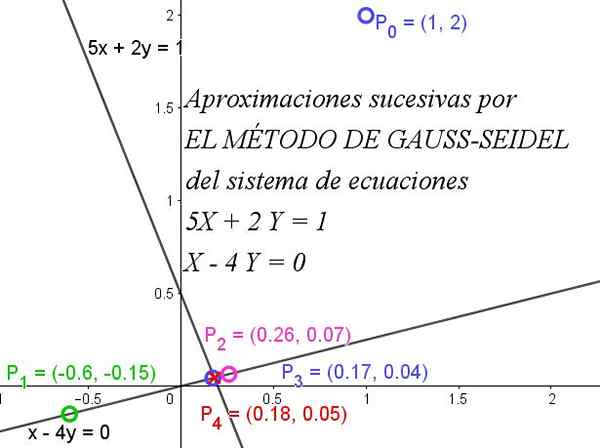
Gambar 1. Metode Gauss-Seidel dengan cepat bertemu untuk mendapatkan sistem persamaan. Sumber: f. Zapata. Untuk pemahaman penuh tentang metode ini, perlu untuk mengetahui bahwa matriks secara diagonal dominan ketika nilai absolut dari elemen diagonal dari setiap baris lebih besar dari atau sama dengan jumlah nilai absolut dari elemen lain dari baris yang sama.
Secara matematis itu dinyatakan sebagai berikut:
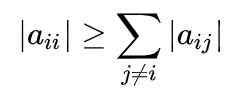
[TOC]
Penjelasan melalui kasus sederhana
Untuk mengilustrasikan apa metode Gauss-Seidel akan mengambil kasus sederhana, di mana Anda dapat menemukan nilai x dan y dalam sistem persamaan linier 2 × 2 yang ditunjukkan di bawah ini:
5x + 2y = 1
X - 4y = 0
Langkah untuk diikuti
1- Pertama-tama Anda harus menentukan apakah konvergensi aman. Segera diamati bahwa, pada dasarnya, ini adalah sistem yang dominan secara diagonal, karena pada baris pertama koefisien pertama memiliki nilai absolut yang lebih besar daripada yang lain dari barisan depan:
| 5 |> | 2 |
Demikian juga, koefisien kedua baris kedua juga dominan secara diagonal:
| -4 |> | 1 |
2- Variabel X dan Y jelas:
X = (1 - 2y)/5
Y = x/4
3- Nilai awal sewenang-wenang ditempatkan, disebut "seed": xo = 1, me = 2.
4
Itu dapat melayani Anda: estimasi berdasarkan intervalX1 = (1 - 2 me)/5 = (1 - 2 × 2)/5 = -3/5
Y1 = x1 / 4 = (-3/5) / 4 = -3/20
5- Lanjutkan dengan cara yang sama untuk mendapatkan perkiraan kedua dari solusi dari sistem persamaan:
X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50
Y2 = x2/4 = (13/50)/4 = 13/200
6- iterasi ketiga:
X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500
Y3 = x3/4 = (87/500)/4 = 87/2000
7- iterasi keempat, sebagai iterasi akhir dari kasus ilustrasi ini:
X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000
Y4 = x4/4 = (913/5000)/4 = 913/20000
Nilai -nilai ini bertepatan dengan solusi yang ditemukan melalui metode resolusi lainnya. Pembaca dapat memeriksanya dengan cepat dengan bantuan program matematika online.
Analisis metode
Seperti dapat dilihat, dalam metode Gauss-Seidel, nilai perkiraan yang diperoleh untuk variabel sebelumnya pada langkah yang sama harus diganti dalam variabel berikut. Ini membedakannya dari metode berulang lainnya seperti Jacobi, di mana setiap langkah membutuhkan pendekatan ke tahap sebelumnya.
Metode Gauss-Seidel bukanlah prosedur paralel, sedangkan Gauss-Jordan. Ini juga merupakan alasan bahwa metode Gauss-Seidel memiliki langkah-langkah yang lebih cepat dari konvergensi-daripada metode Jordan.
Adapun kondisi matriks dominan diagonal, ini tidak selalu puas. Namun, dalam kebanyakan kasus itu cukup untuk menukar jajaran sistem asli untuk memenuhi kondisi tersebut. Selain itu, metode ini hampir selalu menyatu, bahkan ketika kondisi dominasi diagonal tidak terpenuhi.
Hasil sebelumnya, diperoleh dengan empat iterasi dari metode Gauss-Seidel, dapat ditulis dengan cara yang desimal:
Dapat melayani Anda: berapa banyak sumbu simetri yang dimiliki lingkaran?X4 = 0,1826
Y4 = 0,04565
Solusi yang tepat untuk sistem persamaan yang diangkat adalah:
X = 2/11 = 0.1818
Y = 1/22 = 0,04545.
Jadi hanya dengan 4 iterasi hasil yang diperoleh dengan presisi seperseribu (0,001).
Gambar 1 menggambarkan bagaimana iterasi berturut -turut dengan cepat menyatu dengan solusi yang tepat.
Aplikasi
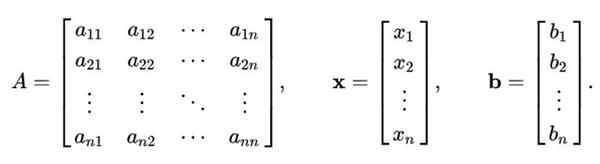
Metode Gauss-Seidel tidak terbatas hanya untuk sistem persamaan linear 2 × 2. Prosedur di atas dapat digeneralisasi untuk menyelesaikan sistem linier N persamaan dengan N tidak diketahui, yang diwakili secara matriks seperti ini:
KE X = B
Di mana KE Itu adalah matriks n x n, ketika X Ini adalah komponen vektor n dari variabel yang akan dihitung; Dan B Itu adalah vektor yang berisi nilai -nilai istilah independen.
Untuk menggeneralisasi urutan iterasi yang diterapkan dalam kasus ilustratif ke sistem n x n, yang ingin menghitung variabel Xi, Formula berikut akan berlaku:
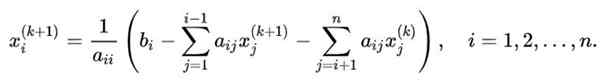
Dalam persamaan ini:
- k Itu adalah indeks untuk nilai yang diperoleh dalam iterasi k.
-K+1 Menunjukkan nilai baru di berikut ini.
Jumlah terakhir dari iterasi ditentukan saat nilai yang diperoleh dalam iterasi K+1 berbeda dari yang diperoleh segera sebelumnya, dalam jumlah ε yang justru ketepatan yang diinginkan.
Contoh metode Gauss-Seidel
- Contoh 1
Tulis algoritma umum yang memungkinkan Anda menghitung vektor solusi perkiraan X dari sistem linier persamaan NXN, mengingat koefisien matriks KE, Vektor istilah independen B, Jumlah iterasi (iter) dan awal atau "benih" dari vektor X.
Larutan
Algoritma ini terdiri dari dua "siklus", satu untuk jumlah iterasi dan yang lainnya untuk jumlah variabel. Itu akan menjadi berikut:
Untuk k ∊ [1 ... iter]
Untuk i ∊ [1 ... n]
X [i]: = (1/a [i, i])*(b [i] - ∑J = 1N(A [i, j]*x [j]) + a [i, i]*x [i])
Dapat melayani Anda: notasi desimal- Contoh 2
Periksa pengoperasian algoritma sebelumnya dengan melamar ke perangkat lunak matematika Studio Smath GRATIS dan GRATIS, Tersedia untuk Windows dan Android. Ambil contoh kasus matriks 2 × 2 yang melayani kami untuk menggambarkan metode Gauss-Seidel.
Larutan
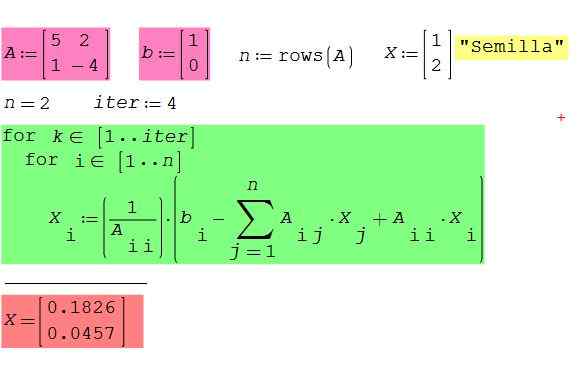Gambar 2. Sistem Persamaan Contoh 2 x 2, menggunakan perangkat lunak Studio Smath. Sumber: f. Zapata. - Contoh 3
Terapkan algoritma Gauss-Seidel untuk sistem persamaan 3 × 3 berikut, yang sebelumnya telah dipesan sedemikian rupa sehingga koefisien diagonal dominan (yaitu, dengan nilai absolut yang lebih besar daripada nilai absolut dari koefisien koefisien dari baris yang sama):
9 x1 + 2 x2 - x3 = -2
7 x1 + 8 x2 + 5 x3 = 3
3 x1 + 4 x2 - 10 x3 = 6
Gunakan vektor nol sebagai benih dan pertimbangkan lima iterasi. Mengomentari hasilnya.
Larutan
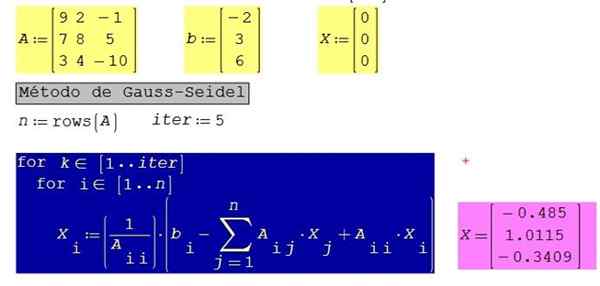Gambar 3. Solusi Sistem Persamaan Contoh 3 yang Diselesaikan, Menggunakan Smath Studio. Sumber: f. Zapata. Untuk sistem yang sama dengan 10 iterasi, bukan 5 hasil berikut diperoleh: x1 = -0.485; X2 = 1.0123; X3 = -0.3406
Ini menunjukkan bahwa itu cukup dengan lima iterasi untuk mendapatkan tiga desimal presisi dan bahwa metode dengan cepat menyampaikan solusi.
- Contoh 4
Dengan menggunakan algoritma Gauss-Seidel yang diberikan, temukan solusi dari sistem persamaan 4 × 4 yang terjadi di bawah ini:
10 x1 - x2 + 2 x3 + 0 x4 = 6
-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25
2 x1 - 1 x2 + 10 x3 - 1 x4 = -11
0 x1 + 3 x2 - 1 x3 + 8 x4 = 15
Untuk memulai metode ini, manfaatkan benih ini:
x1 = 0, x2 = 0, x3 = 0 dan x4 = 0
Pertimbangkan 10 iterasi dan perkirakan kesalahan hasil, dibandingkan dengan nomor iterasi 11.
Larutan
Gambar 4. Solusi Sistem Persamaan Contoh 4 yang Diselesaikan, Menggunakan Smath Studio. Sumber: f. Zapata. Saat membandingkan dengan iterasi berikut (nomor 11), hasilnya identik. Perbedaan terbesar antara kedua iterasi adalah urutan 2 × 10-8, Yang berarti bahwa solusi yang ditampilkan memiliki akurasi setidaknya tujuh desimal.
Referensi
- Metode solusi berulang. Gauss-Seidel. Pulih dari: cimat.MX
- Metode numerik. Gauss-Seidel. Pulih dari: tes.Cua.Uam.MX
- Numeric: Metode Gauss-Seidel. Pulih dari: belajar di linea.Anda.Edu.bersama
- Wikipedia. Metode Gauss-Seidel. Diperoleh dari: di. Wikipedia.com
- Wikipedia. Metode Gauss-Seidel. Pulih dari: is.Wikipedia.com