Multiplikasi pecahan bagaimana hal itu dilakukan, contoh, latihan

Itu Multiplikasi pecahan Ini adalah operasi aritmatika antara dua atau lebih fraksi yang menimbulkan fraksi baru. Pembilangnya melipatgandakan pembilang dari fraksi yang berpartisipasi, dan penyebutnya dengan cara yang sama.

Mari kita lihat dengan contoh di gambar berikut. Misalkan ada dua fraksi A/B dan C/D, dengan B dan D berbeda dari 0.

Gambar 1. Penggandaan fraksi adalah operasi yang dilakukan secara online. Sumber: f. Zapata.

Untuk melaksanakan penggandaan di antara mereka, produk dibuat antara pembilang dan juga dari para penyebut. Dengan cara ini fraksi baru dibuat di mana pembilang dan penyebut masing -masing: (a × c) dan (b × d).

Prosedur ini mudah diperluas ke penggandaan tiga dan lebih banyak pecahan. Mari kita lihat detail lebih lanjut di bawah ini.

Bagaimana penggandaan pecahan dilakukan?

Produk dapat dilambangkan dengan salib atau dengan titik yang diselingi antara fraksi. Selain itu, harus diperhitungkan bahwa pecahan mungkin memiliki tanda positif atau tanda negatif, jadi perlu untuk berhati -hati untuk mengikuti aturan tanda:

-Ketika dua nomor tanda yang sama dikalikan produknya positif.

-Jika dua jumlah tanda berbeda dikalikan, hasilnya negatif.

Cara ini:

Setelah prosedur dilakukan, fraksi disederhanakan, jika memungkinkan. Ini jika pembilang dan penyebut tidak satu sama lain. Misalnya:

Jika pembilang dan penyebut fraksi yang berpartisipasi bukan sepupu satu sama lain, lebih mudah untuk menyederhanakannya sebelum melakukan multiplikasi fraksi. Dengan cara ini, angka yang lebih kecil dan lebih mudah dikelola diperoleh saat menjalankan produk.

Dapat melayani Anda: berapa banyak solusi yang dimiliki persamaan kuadratik?

Sifat penggandaan fraksi

Produk oleh 0

Fraksi apa pun dikalikan 0 sama dengan 0:

Produk oleh 1

Fraksi apa pun dikalikan dengan 1 sama dengan dirinya sendiri:

Oleh karena itu, 1 dipertimbangkan elemen netral perkalian. Perhatikan bahwa seluruh angka 1 memiliki ekspresi fraksional:

Sedemikian rupa sehingga kita dapat berlipat ganda menjadi 1 dengan fraksi apa pun, dengan cara aturan yang sudah dijelaskan. Jadi:

Properti komutatif

Penggandaan fraksi adalah komutatif, yang berarti bahwa urutan faktor tidak mengubah produk:

Properti asosiatif

Penggandaan fraksi juga asosiatif, kami dapat memverifikasi dengan mengalikan tiga fraksi:

Di mana, seperti biasa, penyebut B, D dan F berbeda dari 0.

Dengan kata -kata: Jika kita akan melipatgandakan tiga fraksi, kita dapat memilih untuk membuat produk dari dua yang pertama, dan melipatgandakan hasilnya dengan fraksi ketiga. Atau kalikan dua yang terakhir dan hasilnya akhirnya melipatgandakannya dengan yang pertama dari fraksi.

Apapun perintah yang dipilih, hasilnya akan sama. Mari kita periksa:

Untuk melakukan operasi, dua fraksi pertama dikalikan dari kiri ke kanan. Hasilnya dikalikan dengan fraksi ketiga untuk mendapatkan hasil akhir.

Alternatif lainnya adalah melipatgandakan dua fraksi terakhir, meninggalkan penantian pertama. Pembaca dapat melihat bahwa hasil perantara terdiri dari dua fraksi berbeda dari yang diperoleh dengan cara lain. Tetapi hasil akhirnya sama:

Properti distributif mengenai jumlah tersebut

Biarkan tiga fraksi A/B, C/D dan E/F, dengan B, D dan F berbeda dari 0. Multiplikasi distribusi sehubungan dengan jumlah.

Misalkan kita ingin melakukan operasi berikut:

Cara untuk melaksanakannya, melalui properti ini, adalah sebagai berikut:

Itu dapat melayani Anda: Tukey Test: Apa yang, dalam kasus contoh, latihan terpecahkan

Oleh karena itu, produk angka untuk jumlah dua lainnya, dapat dilakukan dengan menambahkan dua produk: yang pertama untuk yang kedua dan yang pertama dengan yang ketiga. Ini sangat sederhana dengan sebuah contoh:

Hasil akhir tampaknya disederhanakan hingga maksimum, seperti yang dijelaskan di atas.

Contoh

Penggandaan fraksi oleh bilangan bulat

Misalkan Anda ingin melipatgandakan fraksi A/B dengan integer n:

Kami sebelumnya melihat bahwa nomor 1 dapat dinyatakan sebagai fraksi, hanya menempatkan sebagai penyebut di 1. Kita dapat melakukan hal yang sama dengan integer n, karena membaginya dengan 1 tidak mengubahnya sama sekali. Jadi:

Misalnya:

Contoh 2: multiplikasi fraksi dengan angka campuran

Jumlah campuran atau fraksi campuran, adalah bagian yang memiliki seluruh bagian dan bagian pecahan. Untuk melaksanakan produk dari angka seperti itu, baik dengan fraksi, angka campuran lain atau dengan bilangan bulat, perlu mengubahnya secara bergantian menjadi pecahan.

Fraksi yang mewakili angka campuran adalah a Fraksi yang tidak tepat, pembilang yang memiliki nilai absolut yang lebih besar daripada penyebut.

Kita bisa mendapatkannya melalui jumlah seluruh bagian, dengan mudah dinyatakan sebagai fraksi dengan menempatkan 1 sebagai penyebut, ditambah bagian pecahan.

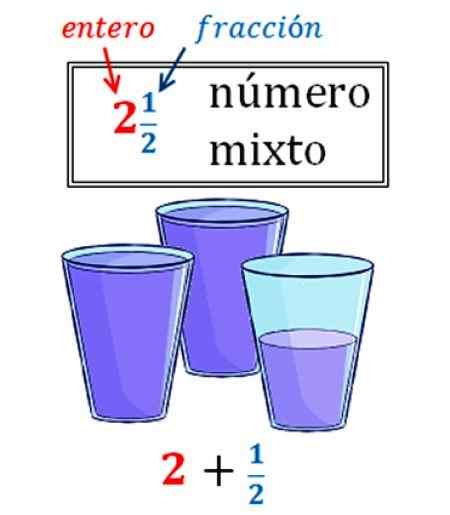Gambar 2. Angka campuran yang diubah menjadi pecahan. Sumber: Wikimedia Commons.

Pada gambar ada contoh angka campuran, yang menunjukkan seberapa sering. Kami memiliki 2 setengah gelas air, yang sebagai angka campuran diekspresikan seperti ini:

2 ½

Kami mendapatkan fraksi yang tidak tepat yang mewakili itu:

Sekarang anggaplah kita ingin menemukan 3/4 bagian dari dua setengah gelas air. Apa yang harus kita lakukan adalah berlipat ganda 3/4 dengan fraksi yang tidak patut diperoleh:

Ini dapat melayani Anda: Distribusi Poisson: Rumus, Persamaan, Model, Properties

Latihan terpecahkan

Latihan 1

Lakukan operasi berikut:

Larutan

Angka 1 ¾ adalah angka campuran. Seluruh bagiannya adalah 1 dan bagian pecahannya adalah ¾. Jika kita melakukan operasi: 1 + ¾, angka campuran diubah menjadi fraksi yang tidak tepat.

1 + ¾ = (4 + 3) /4 = 7/4

Setelah angka campuran dari fraksi yang tidak tepat diubah, operasi multiplikasi dilakukan seperti biasa:

Latihan 2

Usia José adalah ½ dari 2/3 dari usia Manuel. Jika Manuel berusia 24 tahun, berapa usia José?

Larutan

Biarkan X Zaman José, yang tidak diketahui bahwa kita harus menemukan. Pernyataan itu memberi tahu kita bahwa usia Manuel adalah 24 tahun, oleh karena itu nilai ini diketahui.

Untuk menentukan usia José, kami melakukan operasi yang ditunjukkan oleh pernyataan: "Usia José adalah ½ dari 2/3 dari Zaman Manuel".

Ini adalah penggandaan dua pecahan untuk bilangan bulat:

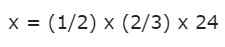
Kami dapat melipatgandakan dua fraksi pertama sesuai dengan aturan yang dijelaskan sebelumnya. Untuk bagiannya, angka 24 adalah bilangan bulat, tetapi kita sudah tahu bahwa tidak ada masalah dalam mengubahnya menjadi sebagian kecil, hanya dengan menempatkan 1 sebagai penyebut:

Kami dapat sangat menyederhanakan operasi, mengamati bahwa 2 dalam pembilang fraksi kedua segera dibatalkan dengan 2 yang merupakan penyebut di yang pertama.

Inilah yang kami tinggalkan setelah pembatalan:

Oleh karena itu José berusia 8 tahun.

Referensi

1. Baldor, a. 1986. Hitung. Edisi dan distribusi Codex.
2. Carena, m. 2019. Manual Matematika. Universitas Nasional Pantai.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Matematika Sangaku. Multiplikasi pecahan. Pulih dari: sangakoo.com.
5. Smartick. Multiplikasi pecahan. Pulih dari: smartick.adalah.