Definisi dan karakteristik sudut nol, contoh, latihan

Dia sudut nol Itu adalah orang yang ukurannya bernilai 0, baik dalam derajat maupun di radian atau sistem pengukuran sudut lainnya. Oleh karena itu tidak memiliki amplitudo atau pembukaan, seperti yang ada di antara dua garis paralel.

Meskipun definisinya terdengar cukup sederhana, sudut nol sangat berguna dalam banyak aplikasi fisika dan teknik, serta dalam navigasi dan desain.

Gambar 1. Antara kecepatan dan percepatan mobil ada sudut nol, oleh karena itu mobil berjalan lebih cepat dan lebih cepat. Sumber: Wikimedia Commons.

Ada jumlah fisik yang harus disejajarkan secara paralel untuk mencapai efek tertentu: jika mobil bergerak lurus di jalan raya dan di antara vektor kecepatannya v dan percepatan vektornya ke Ada 0º, mobil meningkat.

Pada gambar berikut, berbagai jenis sudut muncul termasuk sudut nol di sebelah kanan. Seperti yang dapat dilihat, Angle 0 tidak memiliki amplitudo atau pembukaan.

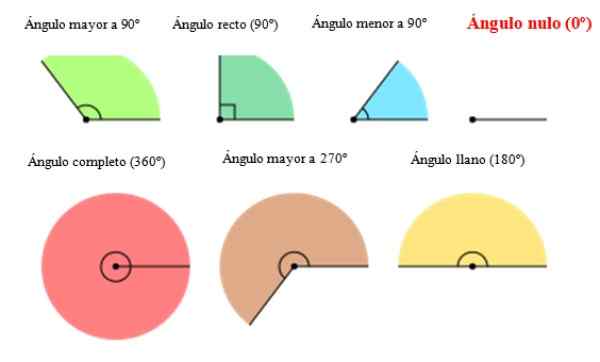Gambar 2. Jenis sudut, termasuk sudut nol. Sumber: Wikimedia Commons. Orias [cc by-sa (https: // createveCommons.Org/lisensi/by-sa/3.0)].[TOC]

Contoh sudut nol

Diketahui bahwa garis paralel membentuk sudut nol. Ketika Anda memiliki garis horizontal, ini sejajar dengan x -sumbu dari sistem koordinat cartesian, oleh karena itu kecenderungannya sehubungan dengan itu adalah 0. Dengan kata lain, garis horizontal memiliki kemiringan nol.

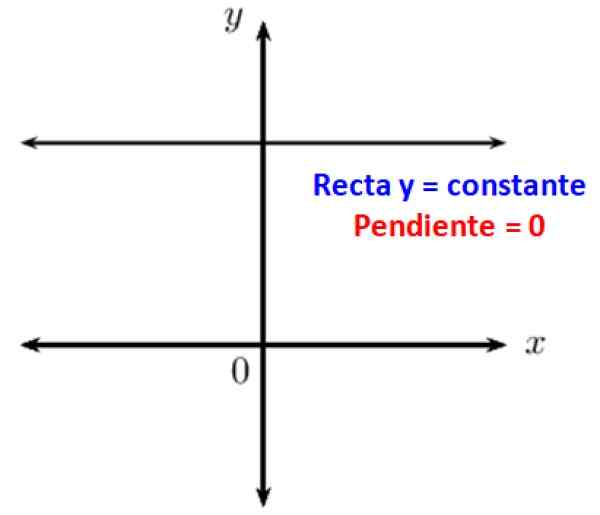Gambar 3. Garis horizontal memiliki nol yang tertunda. Sumber: f. Zapata.

Juga alasan trigonometri sudut nol adalah 0, 1 atau tak terbatas. Oleh karena itu sudut nol hadir dalam banyak situasi fisik yang melibatkan operasi dengan vektor. Alasan ini adalah:

Dapat melayani Anda: pasangan tertib

-Sen 0º = 0

-cos 0º = 1

-TG 0º = 0

-Sec 0º = 1

-Harm 0º → ∞

-CTG 0º → ∞

Dan mereka akan berguna untuk menganalisis beberapa contoh situasi di mana keberadaan sudut nol memainkan peran mendasar:

- Efek sudut nol pada besaran fisik

Jumlah vektor

Ketika dua vektor paralel, sudut di antara mereka adalah nol, seperti yang terlihat pada Gambar 4 di atas. Dalam hal ini, jumlah keduanya dilakukan dengan menempatkan satu demi satu dan besarnya jumlah vektor adalah jumlah besarnya addends (Gambar 4B).

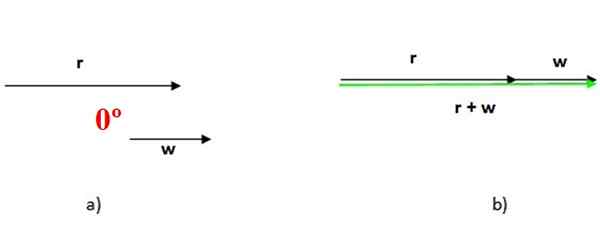Gambar 4. Jumlah vektor paralel, dalam hal ini sudut di antara mereka adalah sudut nol. Sumber: f. Zapata.

Ketika dua vektor paralel, sudut di antara mereka adalah nol, seperti yang terlihat pada Gambar 4 di atas. Dalam hal ini, jumlah keduanya dilakukan dengan menempatkan satu demi satu dan besarnya jumlah vektor adalah jumlah besarnya addends (Gambar 4B)

Torsi atau torsi

Torsi atau torsi menyebabkan rotasi tubuh. Itu tergantung pada besarnya gaya yang diterapkan dan bagaimana hal itu berlaku. Contoh yang sangat representatif adalah kunci bahasa Inggris dari gambar tersebut.

Untuk mencapai efek giliran terbaik, gaya yang tegak lurus berlaku untuk pegangan kunci, baik naik atau turun, tetapi rotasi tidak diharapkan jika gaya paralel dengan pegangan.

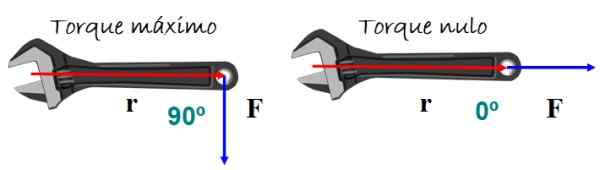Gambar 5. Ketika sudut antara posisi dan vektor kekuatan batal, torsi tidak terjadi dan oleh karena itu tidak ada efek turn. Sumber: f. Zapata.

Secara matematis torsi τ Itu didefinisikan sebagai vektor atau produk silang antara vektor R (Posisi vektor) dan F (Vektor gaya) dari Gambar 5:

Dapat melayani Anda: cabang statistik

τ = r X F

Besarnya torsi adalah:

τ = r f sen θ

Menjadi θ sudut antara R Dan F. Saat sin θ = 0 torsi batal, dalam hal ini θ = 0º (atau juga 180º).

Aliran medan listrik

Aliran medan listrik adalah besarnya skalar yang tergantung pada intensitas medan listrik serta orientasi permukaan yang melaluinya melintasi.

Pada Gambar 6 ada permukaan melingkar area A yang melaluinya garis medan listrik lewat DAN. Orientasi permukaan diberikan oleh vektor normal N. Di sebelah kiri lapangan dan vektor normal membentuk sudut sewenang -wenang akter θ, di tengah mereka membentuk sudut nol dan kanan tegak lurus.

Kapan DAN Dan N Mereka tegak lurus, garis medan tidak melintasi permukaan dan oleh karena itu alirannya nol, sedangkan ketika sudut antara DAN Dan N Itu batal, garis benar -benar melintasi permukaan.

Menunjukkan aliran medan listrik dengan huruf Yunani φ (membaca "fi"), definisi untuk bidang yang seragam seperti pada gambar, tetap seperti ini:

Φ = DAN•NKE

Titik di tengah kedua vektor menunjukkan titik atau produk skalar, yang secara bergantian mendefinisikan:

Φ = DAN•NA = EACOSθ

Tebal dan panah di atas surat itu adalah sumber daya untuk membedakan antara vektor dan besarnya, yang dilambangkan dengan huruf normal. Karena cos 0 = 1, alirannya maksimal saat DAN Dan N Mereka paralel.

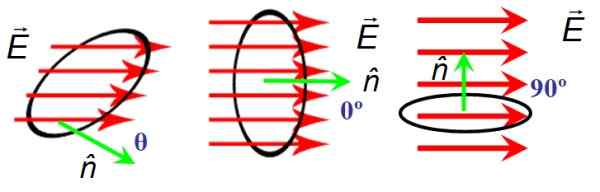Gambar 6. Aliran medan listrik tergantung pada orientasi antara permukaan dan medan listrik. Sumber: f. Zapata.

Latihan

- Latihan 1

Dua kekuatan P Dan Q Mereka bertindak secara bersamaan pada objek X tepat waktu, kedua kekuatan awalnya membentuk sudut θ di antara mereka. Apa yang terjadi pada besarnya gaya yang dihasilkan ketika θ berkurang sampai dibatalkan?

Dapat melayani Anda: evaluasi fungsi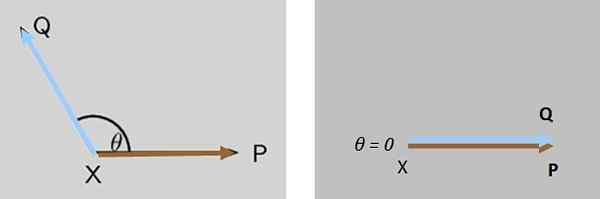 Gambar 7. Sudut antara dua gaya yang bekerja pada tubuh berkurang sampai besarnya gaya yang dihasilkan memperoleh nilai maksimumnya dibatalkan dalam kasus ini. Sumber: f. Zapata.

Larutan

Besarnya gaya yang dihasilkan Q + P Secara bertahap meningkat sampai maksimum saat Q Dan P Mereka benar -benar paralel (Gambar 7 benar).

- Latihan 2

Menunjukkan apakah sudut nol adalah solusi dari persamaan trigonometri berikut:

cos 2x = 1 + 4se x

Larutan

Persamaan trigonometri adalah satu di mana yang tidak diketahui adalah bagian dari argumen dari alasan trigonometri. Untuk menyelesaikan persamaan yang diusulkan, lebih mudah untuk menggunakan rumus untuk cosinus sudut ganda:

cos 2x = cos² X - sen² X

Karena dengan cara ini, argumen di sisi kiri menjadi X alih-alih 2x. Jadi:

cos² X - sen² x = 1 + 4sen x

Di sisi lain cos² X + sen² x = 1, jadi:

cos² X - sen² x = cos² X + sen² x + 4sen x

Istilah cos² X dibatalkan dan tetap:

- Sen² x = sen² x + 4sen x → - 2sen² x - 4senx = 0 → 2sen² x + 4senx = 0

Sekarang perubahan variabel berikutnya dibuat: senx = u dan persamaan diubah menjadi:

2u² + 4U = 0

2u (u+4) = 0

Solusinya adalah: u = 0 dan u = -4. Mengembalikan perubahan kita akan memiliki dua kemungkinan: sin x = 0 dan sen = -4. Solusi terakhir ini tidak layak, karena payudara sudut mana pun adalah antara -1 dan 1, jadi kita dibiarkan dengan alternatif pertama:

sin x = 0

Oleh karena itu x = 0º adalah solusi, tetapi juga menyajikan sudut apa pun yang sininya adalah 0, yang juga bisa 180º (π radianes), 360º (2 π radian) dan masing -masing negatif juga juga.

Solusi paling umum dari persamaan trigonometri adalah: x = kπ di mana k = 0, ± 1, ± 2, ± 3, .. . k nomor integer.

Referensi

1. Baldor, a. 2004. Geometri datar dan ruang dengan trigonometri. Publikasi Budaya s.KE. dari c.V. Meksiko.
2. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 3. Sistem partikel. Diedit oleh Douglas Figueroa (USB).
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 5. Interaksi listrik. Diedit oleh Douglas Figueroa (USB).
4. Onlinemathlearning. Jenis sudut. Diperoleh dari: onlinemathlearning.com.
5. Zill, d. 2012. Aljabar, trigonometri dan geometri analitik. McGraw Hill Inter -American.