Panjang tali (geometri), teorema dan latihan

A tali, Dalam geometri datar, itu adalah segmen garis yang bergabung dengan dua titik dari kurva. Dikatakan bahwa garis yang berisi segmen ini adalah garis pengeringan ke kurva. Ini sering menjadi lingkar, tetapi Anda tentu dapat menarik string ke banyak kurva lain, seperti elips dan perumpamaan.

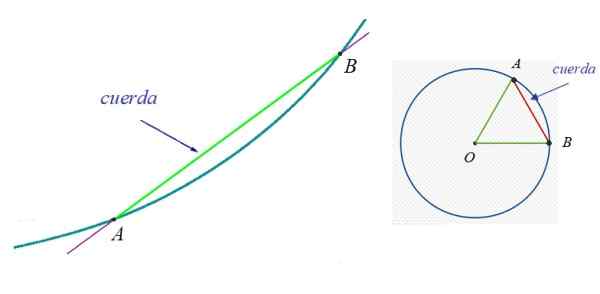
Pada Gambar 1 di sebelah kiri ada kurva, ke titik mana A dan B milik. Tali antara A dan B adalah segmen hijau. Di sebelah kanan adalah lingkar dan salah satu senar mereka, karena dimungkinkan untuk melacak tak terbatas.

Gambar 1. Di sebelah kiri tali kurva sewenang -wenang dan di sebelah kanan tali lingkaran. Sumber: Wikimedia Commons.

Di lingkar diameternya sangat menarik, yang juga dikenal sebagai Tali utama. Ini adalah tali yang selalu berisi pusat keliling dan mengukur dua kali jari -jari.

Gambar berikut diwakili oleh jari -jari, diameter, tali dan juga busur lingkaran. Identifikasi dengan benar masing -masing penting saat menyelesaikan masalah.

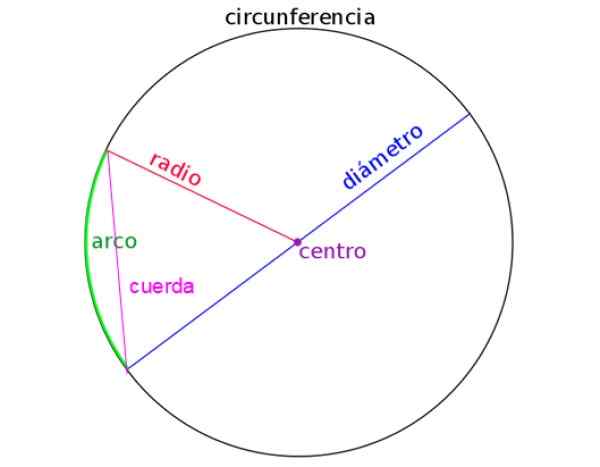Gambar 2. Elemen keliling. Sumber: Wikimedia Commons.

[TOC]

Panjang keliling tali

Kita dapat menghitung panjang tali dalam lingkaran mulai dari Gambar 3a dan 3b. Perhatikan bahwa segitiga selalu dibentuk dengan dua sisi yang sama (Isosceles): segmen OA dan OB, yang mengukur R, jari -jari lingkar. Sisi ketiga dari segitiga adalah segmen AB, disebut C, yang justru panjang tali.

Perlu untuk menarik garis tegak lurus terhadap tali C untuk membagi dua pada sudut θ yang ada antara kedua radio dan yang simpulnya adalah pusat atau kelilingnya. Ini adalah sebuah sudut tengah -Karena simpulnya adalah garis tengah- dan bisector juga merupakan bagian dari keliling.

Itu dapat melayani Anda: sifat radikal

Segera dua persegi panjang terbentuk, yang hipotenusinya. Karena bisector, dan dengan itu diameternya, membelah menjadi dua bagian yang sama dengan tali, ternyata salah satu kaki adalah setengah dari C, seperti yang ditunjukkan pada Gambar 3b.

Dari definisi payudara sudut:

sin (θ/2) = lawan/hypotenusa cateto = (c/2)/r

Karena itu:

sin (θ/2) = c/2r

C = 2R sen (θ/2)

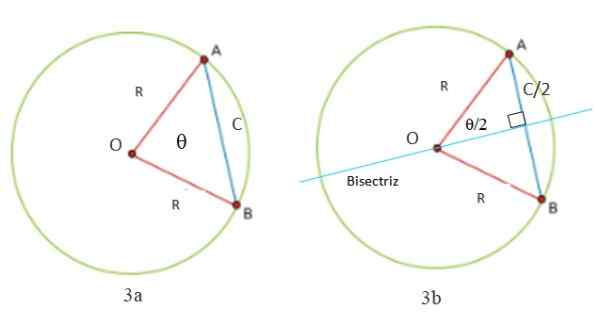Gambar 3. Segitiga yang dibentuk oleh dua radio dan tali keliling adalah Isosceles (Gambar 3), karena memiliki dua sisi yang sama. Bisektor membaginya menjadi dua segitiga persegi panjang (Gambar 3B). Sumber: disiapkan oleh f. Zapata.

Teorema String 

Teorema string mengatakan:

Jika ada dua tali yang berpotongan pada satu titik, produk dari panjang segmen yang muncul di salah satu string, sama dengan produk dari panjang segmen yang didefinisikan pada tali lain.

Gambar berikut menunjukkan dua string dari lingkar yang sama: AB dan CD, yang berpotongan pada titik p. Di tali AB, segmen AP dan PB didefinisikan, sedangkan CP dan PD didefinisikan dalam tali CD. Kemudian, menurut teorema:

Ap . PB = CP . P.S

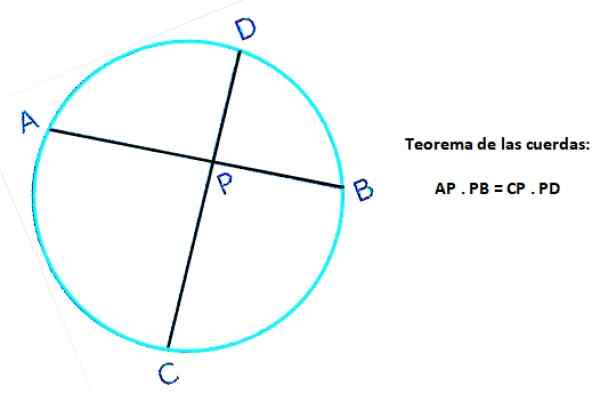Gambar 4. Teorema tali keliling. Sumber: f. Zapata.

Latihan string terpecahkan

- Latihan 1

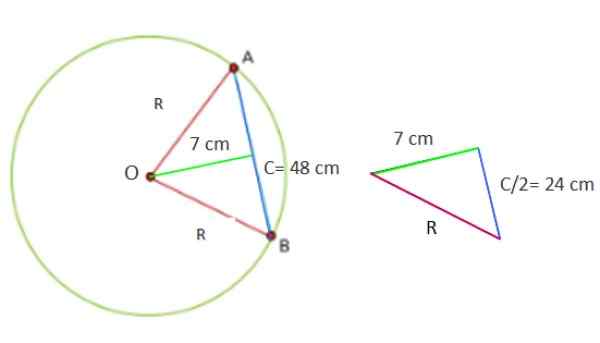
Lingkaran memiliki tali 48 cm, yaitu 7 cm dari tengah. Hitung area lingkaran dan perimeter keliling.

Larutan  

Untuk menghitung lingkaran A area, cukup untuk mengetahui jari -jari keliling ke kotak, karena dipenuhi:

A = π.R²

Sekarang, gambar yang dibentuk dengan data yang disediakan adalah segitiga persegi panjang, yang kakinya masing -masing 7 dan 24 cm.

Gambar 5. Geometri untuk Latihan Terpecahkan 1. Sumber: f. Zapata.

Oleh karena itu untuk menemukan nilai r² Teorema Pythagoras C diterapkan secara langsung² = a² + B², Karena R adalah hipotenus dari segitiga:

Dapat melayani Anda: sudut nol: definisi dan karakteristik, contoh, latihan

R² = (7 cm)² + (24 cm)² = 625 cm²

Maka area yang diminta adalah:

A = π. 625 cm² = 1963.5 cm²

Adapun perimeter atau panjang L dari lingkar, itu dihitung oleh:

L = 2π. R

Mengganti Nilai:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Latihan 2

Tentukan panjang tali lingkaran yang persamaannya adalah:

X² + Dan² - 6x - 14y -111 = 0

Diketahui bahwa koordinat titik tengah tali adalah P (17/2; 7/2).

Larutan

Titik tengah tali P bukan milik lingkar, tetapi titik ekstrem dari tali ya. Masalahnya dapat diselesaikan dengan menggunakan teorema string yang sebelumnya dinyatakan, tetapi pertama -tama nyaman.

Langkah 1: Dapatkan persamaan kanonik dari keliling

Persamaan kanonik keliling dengan pusat (h, k) adalah:

(X-H)² + (Y-K)² = R²

Untuk mendapatkannya, perlu menyelesaikan kotak:

(X² - 6x) + (dan² - 14y) -111 = 0

Perhatikan bahwa 6x = 2.(3x) dan 14y = 2.(7y), sehingga ekspresi sebelumnya ditulis ulang demikian, tidak berubah:

(X² - 6x+3²-3²) + (dan² - 14y+7²-7²) -111 = 0

Dan sekarang, mengingat definisi produk terkenal (A-B)² = a² - 2ab + b² Itu bisa ditulis:

(X - 3)² - 3² + (dan - 7)² - 7² - 111 = 0

= (x - 3)² + (dan - 7)² = 111 + 3² + 7² → (x - 3)² + (dan - 7)² = 169

Lingkar memiliki pusat (3.7) dan radio r = √169 = 13. Gambar berikut menunjukkan grafik lingkar dan string yang akan digunakan dalam teorema:

Dapat melayani Anda: apa 7 elemen keliling?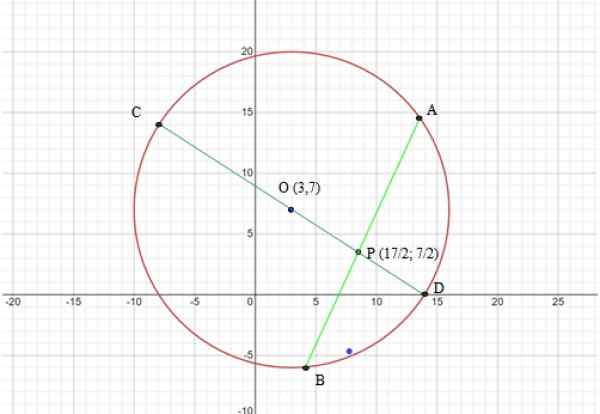Gambar 6. Grafik keliling latihan diselesaikan 2. Sumber: f. Zapata melalui kalkulator grafis online Mathway.

Langkah 2: Tentukan segmen yang akan digunakan dalam teorema string

Segmen yang akan digunakan adalah string CD dan AB, menurut Gambar 6, keduanya dipotong pada titik P, oleh karena itu: oleh karena itu:

Cp . PD = AP. Pb

Sekarang kita akan menemukan jarak antara titik O dan P, karena ini akan memberi kita panjang segmen OP. Jika kami menambahkan jari -jari ke panjang ini, kami akan memiliki segmen CP.

Jarak d_Op Antara dua titik koordinat (x₁,Dan₁) dan (x₂,Dan₂) adalah:

D_Op² = Op² = (x₂ - X₁)² + (Dan₂ - Dan₁)² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

D_Op = Op = √170 /2

Dengan semua hasil yang diperoleh, ditambah grafik, kami membangun daftar segmen berikut (lihat Gambar 6):

CO = 13 cm = r

Op = √170 /2 cm

Cp = op + r = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

Ap = pb

2.Ap = panjang tali

Mengganti dalam teorema string:

Cp . PD = AP . Pb = [(13 +√170 /2) . (13 -√170 /2)] = AP²

[169-170/4] = AP²

253/2 = ap²

AP = √ (253/2)

Panjang tali adalah 2.AP = 2 (√253/2) = √506

Bisakah pembaca memecahkan masalah dengan cara lain?

Referensi

1. Baldor, a. 2004. Geometri datar dan ruang dengan trigonometri. Publikasi Budaya s.KE. dari c.V. Meksiko.
2. C-K12. Lenght akord. Dipulihkan dari: CK12.org.
3. Escobar, J. Kelilingnya. Pulih dari: matematika.Anda.Edu.bersama.
4. Villena, m. Berbentuk kerucut. Diperoleh dari: dspace.Espol.Edu.Ec.
5. Wikipedia. Tali (geometri). Pulih dari: is.Wikipedia.org.