Latihan dan latihan sudut alternatif eksternal diselesaikan

Itu sudut alternatif eksternal Mereka adalah sudut yang terbentuk ketika dua garis paralel dicegat dengan garis pengeringan. Selain sudut ini, torsi lain terbentuk yang disebut sudut alternatif internal.

Perbedaan antara kedua konsep ini adalah kata -kata "eksternal" dan "internal" dan seperti nama yang ditunjukkan, sudut alternatif eksternal adalah kata -kata yang terbentuk di luar dua garis paralel.

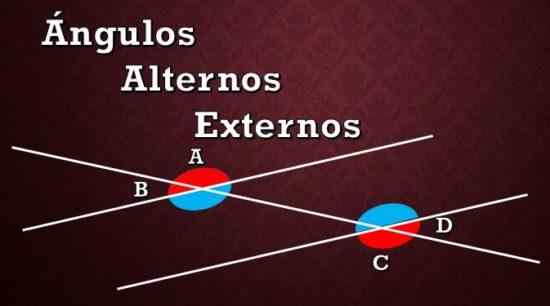
Representasi grafis sudut eksternal alternatif A, B dan C, D

Seperti yang dapat dilihat pada gambar sebelumnya, ada delapan sudut yang terbentuk di antara dua garis paralel dan garis pengeringan. Sudut merah adalah alternatif eksternal, dan sudut biru adalah sudut alternatif internal.

[TOC]

Karakteristik sudut alternatif eksternal

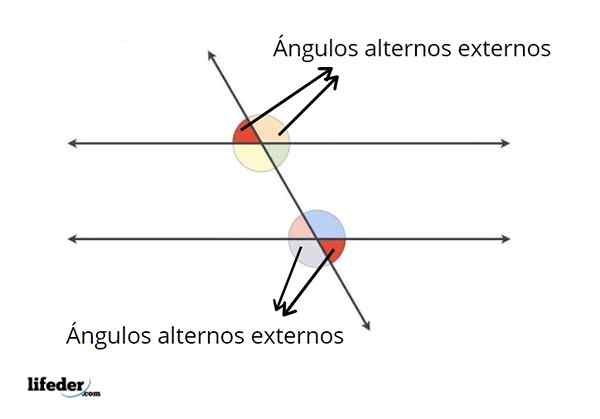Contoh sudut alternatif eksternal

Dalam pendahuluan itu sudah dijelaskan apa sudut alternatif eksternal itu. Selain menjadi sudut eksternal antara paralel, sudut ini memenuhi kondisi lain.

Kondisi yang mereka temui adalah bahwa sudut alternatif eksternal yang dibentuk pada garis paralel adalah kongruen; Ini memiliki ukuran yang sama dengan dua lainnya yang terbentuk di garis paralel lainnya.

Tetapi setiap sudut alternatif eksternal kongruen dengan yang ada di sisi lain dari garis sekte.

Apa sudut alternatif eksternal yang kongruen?

Jika gambar awal dan penjelasan sebelumnya diamati, dapat disimpulkan bahwa sudut alternatif eksternal yang sesuai satu sama lain adalah: sudut A dan C, dan sudut B dan D.

Untuk menunjukkan bahwa mereka kongruen.

Dapat melayani Anda: fungsi konstan: karakteristik, contoh, latihan

Latihan terpecahkan

Di bawah ini adalah serangkaian latihan di mana definisi dan properti kongruensi sudut alternatif eksternal harus diterapkan.

Latihan Pertama

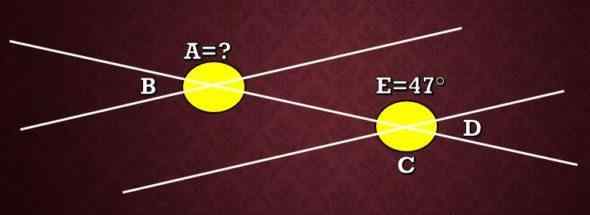
Pada gambar berikut, apa ukuran sudut yang mengetahui bahwa sudut E mengukur 47 °?

Larutan

Seperti yang dijelaskan sebelumnya, Angles A dan C adalah kongruen karena menjadi alternatif eksternal. Oleh karena itu, ukuran a sama dengan ukuran c. Sekarang, karena sudut E dan C adalah sudut yang berlawanan dengan simpul, mereka memiliki bahwa mereka memiliki ukuran yang sama, oleh karena itu, ukuran C adalah 47 °.

Kesimpulannya, ukurannya sama dengan 47 °.

Latihan kedua

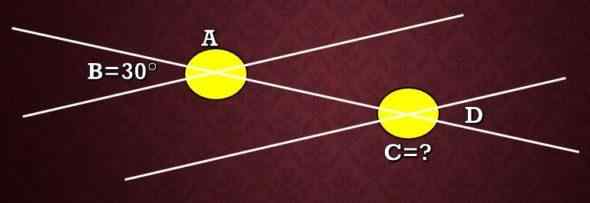
Hitung ukuran sudut C yang ditunjukkan pada gambar berikut, mengetahui bahwa sudut B mengukur 30 °.

Larutan

Dalam contoh ini, definisi digunakan. Dua sudut bersifat tambahan jika jumlah tindakannya sama dengan 180 °.

Pada gambar dapat dilihat bahwa A dan B adalah tambahan, oleh karena itu A+B = 180 °, yaitu, pada+30 ° = 180 ° dan oleh karena itu A = 150 °. Sekarang, seperti A dan C mereka adalah sudut alternatif eksternal, jadi langkahnya sama. Oleh karena itu, ukuran C adalah 150 °.

Latihan ketiga

Pada gambar berikut, ukuran sudut A adalah 145 °. Apa ukuran sudut e?

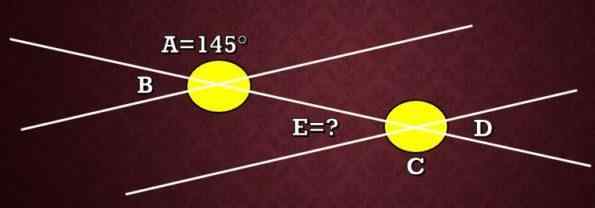
Larutan

Pada gambar dapat dilihat bahwa sudut A dan C adalah sudut alternatif eksternal, oleh karena itu, mereka memiliki ukuran yang sama. Artinya ukuran C adalah 145 °.

Karena sudut C dan E adalah sudut tambahan, ia harus C+E = 180 °, yaitu 145 °+E = 180 ° dan oleh karena itu ukuran sudut E adalah 35 °.

Dapat melayani Anda: Kesalahan pengambilan sampel: Rumus dan persamaan, perhitungan, contoh

Referensi

1. Bourke. (2007). Buku Kerja Geometri Matematika Geometri. Pembelajaran Newpath.
2. C. DAN. KE. (2003). Elemen Geometri: Dengan banyak latihan dan geometri kompas. Universitas Medellin.
3. Clemens, s. R., O'DAFER, hlm. G., & Cooney, T. J. (1998). Geometri. Pendidikan Pearson.
4. Lang, s., & Murrow, G. (1988). Geometri: kursus sekolah menengah. Sains Springer & Media Bisnis.
5. Lira, a., Jaime, hlm., Chavez, m., Gallegos, m., & Rodríguez, C. (2006). Geometri dan Trigonometri. Edisi Umbral.
6. Moyano, a. R., Saro, a. R., & Ruiz, R. M. (2007). Aljabar dan geometri kuadratik. Netbiblo.
7. Palmer, c. yo., & Bibb, s. F. (1979). Matematika Praktis: Aritmatika, Aljabar, Geometri, Trigonometri dan Aturan Perhitungan. Kembali.
8. Sullivan, m. (1997). Trigonometri dan geometri analitik. Pendidikan Pearson.
9. Wingard-Eselson, r. (2012). Geometri. Enslow Publishers, Inc.