Komponen persegi panjang dari vektor (dengan latihan)

Itu komponen persegi panjang dari vektor adalah data yang membentuk vektor ini. Untuk menentukannya, perlu memiliki sistem koordinat, yang biasanya merupakan bidang Cartesian.

Setelah Anda memiliki vektor dalam sistem koordinat, komponennya dapat dihitung. Ini adalah 2, komponen horizontal (sejajar dengan sumbu x), yang disebut "komponen dalam sumbu x", dan komponen vertikal (sejajar dengan sumbu y), yang disebut "komponen dalam sumbu y" ".

Representasi grafis dari komponen persegi panjang dari vektor

Untuk menentukan komponen, itu perlu.

[TOC]

Bagaimana menentukan komponen persegi panjang dari vektor?

Untuk menentukan komponen -komponen ini, hubungan tertentu antara persegi panjang dan fungsi trigonometri harus diketahui.

Pada gambar berikut Anda dapat melihat hubungan ini.

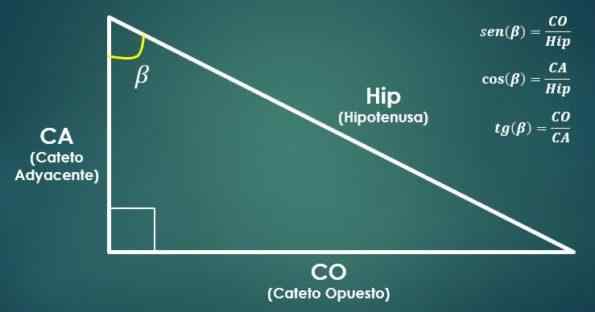Hubungan antara persegi panjang dan fungsi trigonometri

Bosom sudut sama dengan hasil bagi antara ukuran cateto yang bertentangan dengan sudut dan ukuran hipotenusus.

Di sisi lain, kosinus sudut sama dengan hasil bagi antara ukuran cateto yang berdekatan dengan sudut dan ukuran hypotenuse.

Singgung sudut sama dengan hasil bagi antara ukuran kaki yang berlawanan dan ukuran cateto yang berdekatan.

Dalam semua hubungan ini perlu untuk menetapkan segitiga persegi panjang yang sesuai.

Apakah ada metode lain?

Ya. Bergantung pada data yang disediakan, cara untuk menghitung komponen persegi panjang vektor dapat bervariasi. Alat lain yang banyak digunakan adalah Teorema Pythagoras.

Dapat melayani Anda: Teorema Keberadaan dan Keunikan: Demonstrasi, Contoh dan Latihan

Latihan terpecahkan

Latihan berikut mempraktikkan definisi komponen persegi panjang dari vektor dan hubungan yang dijelaskan di atas.

Latihan Pertama

Diketahui bahwa vektor A memiliki besarnya sama dengan 12 dan sudut yang bentuknya dengan sumbu x memiliki ukuran 30 °. Menentukan komponen persegi panjang dari vektor tersebut.

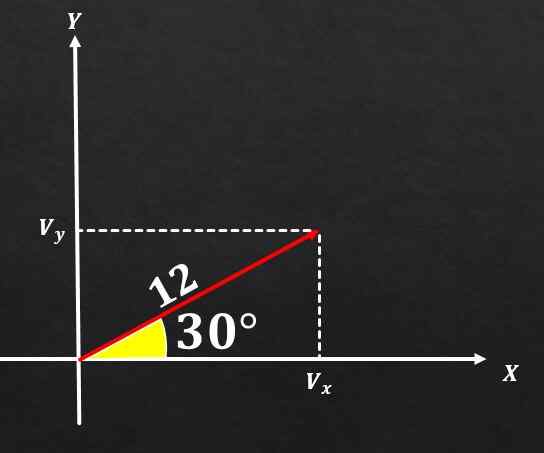
Larutan

Jika gambar dihargai dan rumus yang dijelaskan di atas digunakan, dapat disimpulkan bahwa komponen dalam dan vektor A sama dengan

sin (30 °) = Vy / 12, dan karenanya Vy = 12*(1/2) = 6.

Di sisi lain, komponen pada sumbu x vektor A sama dengan

cos (30 °) = vx / 12, dan oleh karena itu vx = 12*(√3 / 2) = 6√3.

Latihan kedua

Jika vektor A memiliki besarnya sama dengan 5 dan komponen pada sumbu x sama dengan 4, tentukan nilai komponen A pada sumbu y Y.

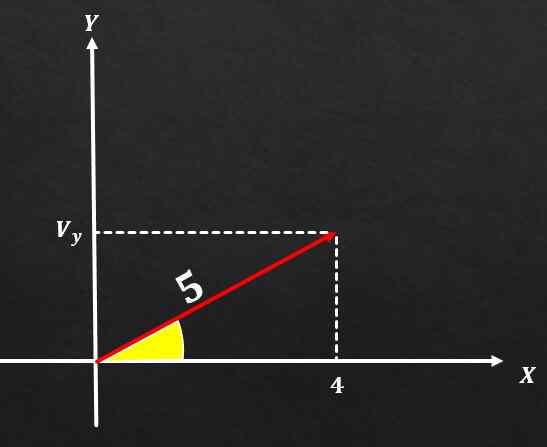
Larutan

Menggunakan teorema Pythagoras, besarnya vektor, kuadrat tinggi harus sama dengan jumlah kuadrat dari dua komponen persegi panjang. Yaitu, m² = (vx) ² + (vy) ².

Mengganti nilai yang disediakan, Anda harus

5² = (4) ² + (Vy) ², oleh karena itu, 25 = 16 + (Vy) ².

Ini menyiratkan bahwa (vy) ² = 9 dan akibatnya vy = 3.

Latihan ketiga

Jika vektor A memiliki besarnya sama dengan 4 dan ini membentuk sudut 45 ° dengan sumbu x, tentukan komponen persegi panjang dari vektor tersebut.

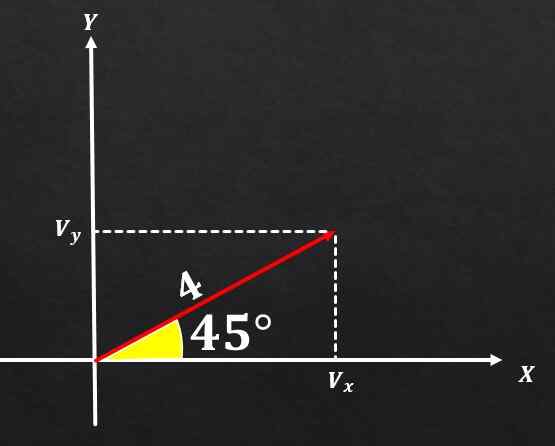
Larutan

Menggunakan hubungan antara segitiga persegi panjang dan fungsi trigonometri, dapat disimpulkan bahwa komponen pada dan vektor A sama dengan

sin (45 °) = vy / 4, dan karenanya vy = 4*(√2 / 2) = 2√2.

Di sisi lain, komponen pada sumbu x vektor A sama dengan

Dapat melayani Anda: suksesi majemuk

cos (45 °) = vx / 4, dan karenanya vx = 4*(√2 / 2) = 2√2.

Referensi

1. Landaverde, f. D. (1997). Geometri (Cetak ulang ed.). Kemajuan.
2. Dibocorkan. (2006). segitiga (Illustrated ed.). Heinemann-Raintree.
3. Pérez, c. D. (2006). Prekalkulasi. Pendidikan Pearson.
4. Ruiz, á., & Barrantes, h. (2006). Geometri. Teknologi CR.
5. Sullivan, m. (1997). Prekalkulasi. Pendidikan Pearson.
6. Sullivan, m. (1997). Trigonometri dan geometri analitik. Pendidikan Pearson.