Sudut pelengkap yang dan bagaimana dihitung, contoh, latihan
- 3558
- 326
- Ernesto Mueller
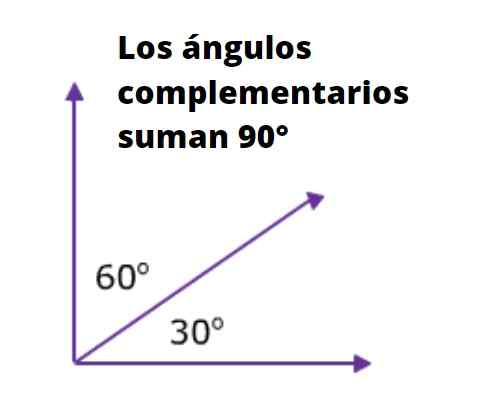
Dua atau lebih sudut sudut komplementer Jika jumlah langkahnya sesuai dengan sudut kanan. Seperti diketahui, ukuran sudut kanan dalam derajat adalah 90º, dan di Radianes adalah π/2.
Sebagai contoh, dua sudut yang berdekatan dengan hipotenus dari segitiga persegi panjang saling melengkapi, karena jumlah tindakan mereka adalah 90º. Gambar berikut sangat ilustratif tentang hal itu:
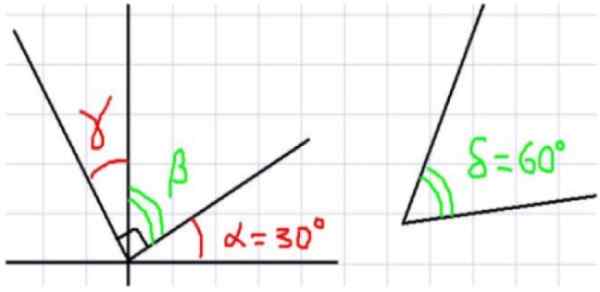Gambar 1. Di sebelah kiri, beberapa sudut dengan titik umum. Di sebelah kanan sudut 60º yang melengkapi sudut α (alpha). Sumber: f. Zapata. Gambar 1 menunjukkan total empat sudut. α dan β saling melengkapi bersebelahan dan jumlah penuh sudut kanan. Demikian pula β adalah komplementer untuk γ, di mana ia mengikuti bahwa γ dan α memiliki ukuran yang sama.
Sekarang, karena jumlah α dan Δ sama dengan 90 derajat, dapat dikatakan bahwa α dan δ adalah komplementer. Selain itu, karena β dan δ memiliki α komplementer yang sama, dapat dikatakan bahwa β dan Δ memiliki ukuran yang sama.
[TOC]
Contoh sudut komplementer
Dalam contoh -contoh berikut ini diminta untuk menemukan sudut yang tidak diketahui, ditunjukkan dengan interogasi pada Gambar 2.
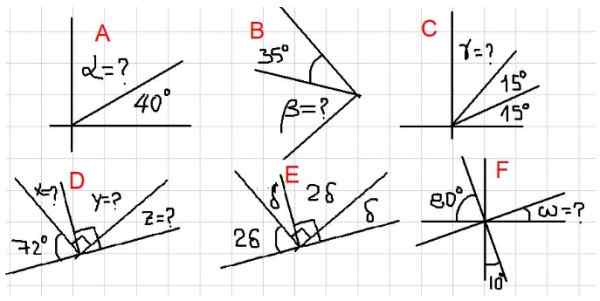Gambar 2. Berbagai contoh sudut komplementer. Sumber: f. Zapata. - Contoh A, B dan C
Contoh -contoh berikut adalah dalam urutan kompleksitas.
Contoh a
Pada gambar atas kita memiliki sudut yang berdekatan α dan 40º Tambahkan ke sudut kanan. Yaitu α + 40º = 90º, oleh karena itu α = 90º- 40º = 50º.
Contoh b
Karena β saling melengkapi dengan sudut 35º, maka β = 90º - 35º = 55º.
Dapat melayani Anda: orthoedro: rumus, area, volume, diagonal, contohContoh c
Dari Gambar 2C, jumlah γ + 15º + 15º = 90º. Artinya γ komplementer untuk sudut 30 = 15º + 15º. Sehingga:
γ = 90º- 30º = 60º
- Contoh D, E dan F
Dalam contoh -contoh ini ada lebih banyak sudut yang terlibat. Untuk menemukan yang tidak diketahui, pembaca harus menerapkan konsep sudut komplementer sebanyak yang diperlukan.
Contoh d
Karena x komplementer dengan 72º, maka x = 90º - 72º = 18º. Selain itu dan komplementer dengan x, lalu y = 90º - 18º = 72º.
Akhirnya Z saling melengkapi. Dari semua hal di atas itu mengikuti itu:
Z = 90º - 72º = 18º
Contoh e
Sudut Δ dan 2Δ adalah komplementer, oleh karena itu Δ + 2Δ = 90º.
Yaitu 3Δ = 90º, yang menyiratkan bahwa Δ = 90º / 3 = 30º.
Contoh f
Jika kita menyebut sudut antara Ω dan 10, itu kemudian harus dilengkapi dengan mereka, karena diamati bahwa jumlah lengkap mereka sudut kanan. Dimana itu u = 80º. Karena u komplementer dengan Ω, maka Ω = 10º.
Latihan
Tiga latihan diusulkan di bawah ini. Di semua dari mereka nilai sudut A dan B harus ditemukan dalam derajat, sehingga hubungan yang ditunjukkan pada Gambar 3 terpenuhi.
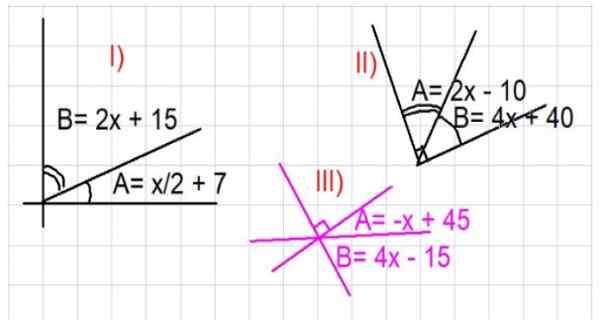Gambar 3. Ilustrasi untuk latihan sudut pelengkap. Sumber: f. Zapata. - Latihan 1
Tentukan nilai sudut A dan B dari Bagian I) dari Gambar 3.
Larutan
Dari gambar yang ditunjukkan terlihat bahwa A dan B saling melengkapi, oleh karena itu A + B = 90º. Ekspresi A dan B digantikan sebagai fungsi x yang diberikan di Bagian I):
Dapat melayani Anda: Radio Konvergensi: Definisi, Contoh dan Latihan Diselesaikan(x/2 + 7) + (2x + 15) = 90
Maka istilah tersebut dikelompokkan dengan benar dan persamaan linier sederhana diperoleh:
(5x/2) + 22 = 90
Mengurangi 22 di kedua anggota adalah:
5x/2 = 90 -22 = 68
Dan akhirnya nilai x dibersihkan:
x = 2*68/5 = 136/5
Sekarang sudut ditemukan mengganti nilai x:
A = (136/5)/2 +7 = 103/5 = 20.6 º.
Sedangkan sudut B adalah:
B = 2*136/5 + 15 = 347/5º = 69.4º .
- Latihan 2
Temukan nilai sudut A dan B dari gambar II, Gambar 3.
Larutan
Sekali lagi, karena A dan B adalah sudut komplementer, Anda harus: A + B = 90º. Mengganti ekspresi A dan B sebagai fungsi x yang diberikan pada Bagian II) dari Gambar 3 adalah:
(2x - 10) + (4x +40) = 90
Istilah serupa dikelompokkan untuk mendapatkan persamaan:
6 x + 30 = 90
Membagi kedua anggota antara 6 diperoleh:
x + 5 = 15
Di mana itu mengikuti x = 10º.
Karena itu:
A = 2*10 - 10 = 10º
B = 4*10 + 40 = 80º.
- Latihan 3
Tentukan nilai sudut A dan B dari Bagian III) dari Gambar 3.
Larutan
Angka tersebut dianalisis dengan cermat untuk mencari sudut komplementer. Dalam hal ini Anda harus + B = 90 derajat. Mengganti ekspresi A dan B sebagai fungsi x yang diberikan pada gambar, Anda memiliki:
(-X +45) + (4x -15) = 90
3 x + 30 = 90
Membagi kedua anggota dengan 3 adalah sebagai berikut:
x + 10 = 30
Di mana ia mengikuti x = 20º.
Artinya sudut A = -20 +45 = 25º. Dan untuk bagiannya: b = 4*20 -15 = 65º.
Sudut sisi tegak lurus
Dikatakan bahwa dua sudut Sisi tegak lurus Jika masing -masing pihak memiliki tegak lurus yang sesuai di sisi lain. Gambar berikut mengklarifikasi konsep:
Dapat melayani Anda: suksesi majemuk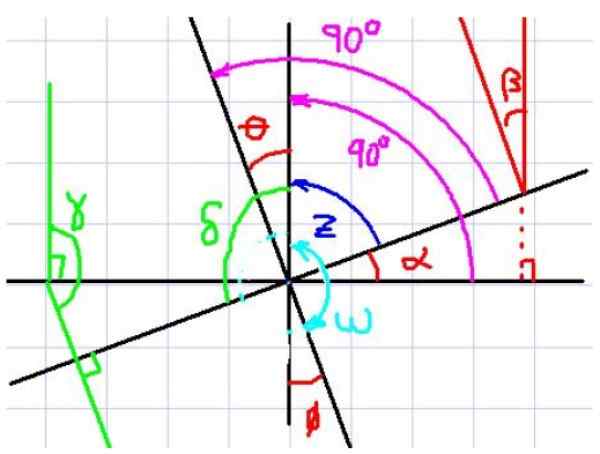
Gambar 4. Sudut sisi tegak lurus. Sumber: f. Zapata. Pada Gambar 4 sudut α dan θ diamati, misalnya. Sekarang perhatikan bahwa setiap sudut memiliki tegak lurus yang sesuai di sudut lainnya.
Juga terlihat bahwa α dan θ memiliki sudut komplementer yang sama z, Oleh karena itu pengamat segera menyimpulkan bahwa α dan θ memiliki ukuran yang sama. Tampaknya jika dua sudut memiliki sisi tegak lurus satu sama lain, mereka sama, tetapi mari kita lihat kasus lain.
Sekarang pertimbangkan sudut α dan Ω. Kedua sudut ini juga memiliki sisi tegak lurus yang sesuai, namun tidak dapat dikatakan bahwa mereka memiliki ukuran yang sama, karena yang satu akut dan yang lainnya tumpul.
Perhatikan bahwa Ω + θ = 180º. Selain θ = α. Jika Anda mengganti ekspresi z ini dalam persamaan pertama yang Anda dapatkan:
Δ + α = 180º, menjadi Δ dan α adalah sudut dari sisi yang saling tegak lurus.
Aturan umum untuk sudut sisi tegak lurus
Dari yang disebutkan di atas, aturan yang selalu terpenuhi bahwa sudut -sudut memiliki sisi tegak lurus dapat ditetapkan:
Jika dua sudut adalah sisi yang saling tegak lurus, maka mereka sama jika keduanya akut atau keduanya tumpul. Kalau tidak, jika yang satu akut dan yang lainnya tumpul, maka mereka tambahan, yaitu, mereka menambahkan 180º.
Menerapkan aturan ini dan mengacu pada sudut Gambar 4 kita dapat menegaskan yang berikut:
α = β = θ = φ
γ = δ
Dengan sudut tambahan α α, β, θ dan φ.
Referensi
- Baldor, j. KE. 1973. Geometri datar dan ruang. Budaya Amerika Tengah.
- Hukum dan Rumus Matematika. Sistem Pengukuran Sudut. Diperoleh dari: ingemecanica.com.
- Wentworth, g. Geometri planet. Pulih dari: Gutenberg.org.
- Wikipedia. Sudut komplementer. Pulih dari: is.Wikipedia.com
- Wikipedia. Konveyor. Pulih dari: is.Wikipedia.com
- Zapata f. Goniometer: Sejarah, Bagian, Operasi. Diperoleh dari: Lifer.com