Sifat simetri pusat, contoh dan latihan

Dua poin A dan 'memiliki Simetri Tengah Mengenai suatu titik atau ketika segmen AA 'melewatinya dan juga titik tengah AA'. To the point atau dipanggil Pusat Simetri.

Simetris pusat dari segitiga ABC sehubungan dengan satu titik atau, adalah segitiga lain a'b'c 'yang memiliki karakteristik berikut:

-Segmen homolog adalah panjang yang sama 

-Sudut yang sesuai memiliki ukuran yang sama.

Gambar 1. ABC Triangle dan A'B'C Simetrisnya '. Sumber: f. Zapata.

Pada Gambar 1 A ABC Triangle (Merah) dan Simetris Pusat A'B'C '(hijau), sehubungan dengan pusat simetri atau. 

Dalam gambar yang sama ini, pengamat yang penuh perhatian akan menyadari bahwa hasil yang sama diperoleh dengan menerapkan rotasi segitiga asli, selama itu 180º dan fokus pada atau.

Oleh karena itu, simetri pusat setara dengan belokan 180º sehubungan dengan pusat simetri.

[TOC]

Sifat simetri pusat

Simetri pusat memiliki sifat -sifat berikut:

-Pusat simetri adalah titik tengah segmen yang bergabung dengan suatu titik dengan simetrisnya.

-Titik simetris yang lain yang terletak di pusat simetri, bertepatan dengan pusat simetri.

-Simetris pusat segitiga adalah segitiga kongruen (sama) dengan aslinya.

-Gambar dengan simetri pusat lingkar adalah lingkar lain dari jari -jari yang sama.

-Lingkaran memiliki simetri pusat sehubungan dengan pusatnya sendiri.

Gambar 2. Desain dengan simetri pusat. Sumber: Pixabay.

-Elips memiliki simetri pusat sehubungan dengan pusatnya.

-Segmen memiliki simetri pusat sehubungan dengan titik tengahnya.

-Segitiga sama sisi tidak memiliki simetri pusat sehubungan dengan pusatnya, karena simetrisnya, meskipun kongruen dengan yang pertama, memberikan segitiga sama sisi yang diputar.

Itu dapat melayani Anda: y = 3sen (4x) periode fungsi

-Kotak memiliki simetri sentral sehubungan dengan pusatnya.

-Pentagon tidak memiliki simetri sentral sehubungan dengan pusatnya.

-Poligon biasa memiliki simetri sentral ketika mereka memiliki sejumlah sisi torsi.

Contoh

Kriteria simetri memiliki banyak aplikasi dalam sains dan teknik. Simetri pusat hadir di alam, misalnya kristal es dan sarang laba -laba memiliki jenis simetri ini.

Selain itu, banyak masalah yang mudah diselesaikan ketika keberadaan simetri pusat dan jenis simetri lainnya digunakan. Oleh karena itu lebih mudah untuk mengidentifikasi dengan cepat saat itu terjadi.

Gambar 3. Kristal es memiliki simetri pusat. Sumber: Pixabay.

Contoh 1

Diberi titik P koordinat (a, b), Anda harus menemukan koordinat p 'simetris mengenai asal atau koordinat (0, 0).

Hal pertama adalah membangun p 'p', yang ditarik garis yang melewati asal atau dan melalui titik p. Persamaan baris ini adalah y = (b/a) x.

Sekarang mari kita sebut (a ', b') koordinat titik simetris p '. Poin hal. Selain itu, jarak OP harus sama dengan OP ', yang secara analitik menulis seperti ini:

√ (a² + B²) = √ (a '² + B '² )

Berikut ini adalah menggantikan b '= [(b/a).A '] dalam ekspresi sebelumnya dan kuadrat di kedua sisi kesetaraan untuk menghilangkan akar kuadrat: (a² + B²) = [a '² + (B²/ke²).ke'²]

Dengan mengekstraksi faktor umum dan menyederhanakan, itu tercapai² = a². Persamaan ini memiliki dua solusi nyata: a '= +a atau a' = -a. 

Untuk mendapatkan b ', kami menggunakan lagi b' = (b/a) a '. Jika solusi positif dari A diganti, tercapai bahwa b '= b. Dan saat solusi negatif diganti, lalu b '= -b. 

Dapat melayani Anda: apa 7 elemen keliling?

Solusi positif memberi untuk p 'poin yang sama p, jadi itu dikesampingkan. Solusi negatif jelas menawarkan koordinat titik simetris:

P ': (-a, -b)

Contoh 2

Diperlukan untuk menunjukkan bahwa segmen AB dan pusat simetrisnya memiliki panjang yang sama.

Dimulai dengan koordinat titik A, yaitu (kapak, ay) dan titik -titik b: (bx, oleh), panjang ab diberikan oleh:

D (ab) = √ ((bx - ax)² + (Oleh - ay)² )

Dengan analogi, segmen simetris a'b 'akan memiliki panjang yang diberikan oleh:

d (a'b ') = √ ((bx' - ax ')² + (Oleh ' - ay')² )

Koordinat titik simetris a 'adalah kapak' = -ax dan ay '= -ay. Demikian pula yang dari B 'adalah bx' = -bx dan oleh '= -by. Jika koordinat ini diganti dalam persamaan jarak d (a'b ') yang Anda miliki:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) Itu setara dengan:

 √ ((bx - kapak)² + (Oleh - ay)²) = D (AB)

Ditunjukkan bahwa kedua segmen memiliki panjang yang sama.

Latihan terpecahkan

- Latihan 1

Menunjukkan secara analitis bahwa simetris pusat atau lingkaran jari -jari R dan pusat atau, adalah lingkar asli yang sama.

Larutan

Persamaan radius R dan lingkaran tengah (0,0) adalah:

X² + Dan² = R² (Persamaan keliling c)

Jika pada setiap titik p dari lingkar dan koordinat (x, y) koordinat simetris p ') ditemukan, persamaan lingkar simetris adalah:

X '² + Dan'² = R² (Persamaan Lingkar Simetris C ')

Sekarang kami merujuk pada hasil Contoh 1, yang menyimpulkan bahwa koordinat titik p ', simetris ke p dan koordinat (a, b), adalah (-a, -b). 

Tetapi dalam latihan ini, titik P memiliki koordinat (x, y), sehingga p simetrisnya akan memiliki koordinat x '= -x e y' = -y. Mengganti ini dalam persamaan lingkar simetris adalah:

Dapat melayani Anda: rhomboid: karakteristik, cara mengeluarkan perimeter dan area

(-X)² + (-Dan)² = R²

Yang setara dengan: x²+ Dan² = R², menyimpulkan bahwa simetris pusat lingkaran sehubungan dengan pusatnya adalah keliling itu sendiri.

- Latihan 2

Tunjukkan dengan cara geometris bahwa simetri pusat menjaga sudut.

Larutan

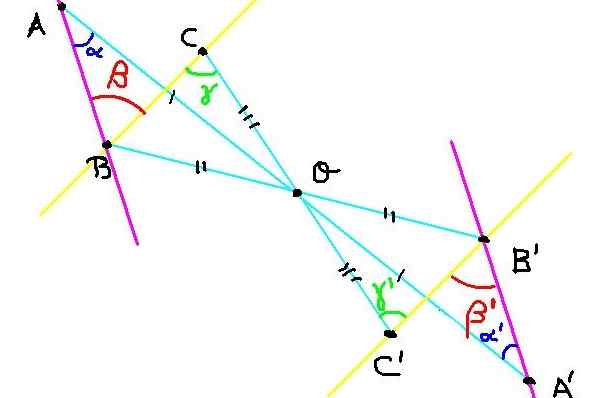Gambar 4. Konstruksi titik simetris untuk Latihan 2. Sumber: f. Zapata.

Ada tiga titik A, B dan C di pesawat. A -nya A ', B' dan C 'dibangun sehubungan dengan pusat simetri atau, seperti yang ditunjukkan pada Gambar 4. 

Sekarang kita harus menunjukkan bahwa sudut ∡Abc = β memiliki ukuran yang sama dengan sudut ∡a'b'c '= β' '.

Karena c dan c 'simetris, maka oc = oc'. Demikian pula ob = ob 'y oa = oa'. Di sisi lain, sudut ∡boc = ∡b'oc 'karena menentang simpul.

Kemudian segitiga Boc dan B'oc 'adalah kongruen karena memiliki sudut yang sama antara dua sisi yang sama.

Karena Boc kongruen ke B'oc 'maka sudutnya  γ Dan γ ' Mereka sama. Tapi sudut ini, selain memuaskan γ = γ ' Mereka adalah alternatif internal antara garis BC dan B'C 'yang menyiratkan bahwa garis BC sejajar dengan B'C'.

Demikian pula Baa kongruen dengan b'oa 'dari apa yang diikuti α = α ' . Tetapi  α Dan α ' Mereka adalah sudut alternatif internal antara garis Ba dan B'a, yang disimpulkan bahwa garis BA sejajar dengan B'a '.

Karena sudut ∡ABC = β memiliki sisi paralelnya dengan sudut ∡a'b'c '= β' dan juga keduanya akut disimpulkan bahwa:

∡Abc = ∡a'b'c '= β = β' '

Menunjukkan dengan cara ini bahwa simetri pusat mempertahankan ukuran sudut.

Referensi

1. Baldor, j. KE. 1973.Geometri datar dan ruang. Budaya Amerika Tengah. 
2. Hukum dan Rumus Matematika. Sistem Pengukuran Sudut. Diperoleh dari: ingemecanica.com.
3. Wentworth, g. Geometri planet. Pulih dari: Gutenberg.org.
4. Wikipedia. Simetri Tengah. Pulih dari: is.Wikipedia.com
5. Wikipedia. Konveyor. Pulih dari: is.Wikipedia.com
6. Zapata f. Sudut konjugat internal dan eksternal. Diperoleh dari: Lifer.com