Sudut dalam jenis keliling, sifat, latihan diselesaikan

Ditelepon Sudut keliling kepada mereka di mana salah satu elemennya atau berpotongan di lingkar yang diberikan. Di antara mereka adalah sebagai berikut:

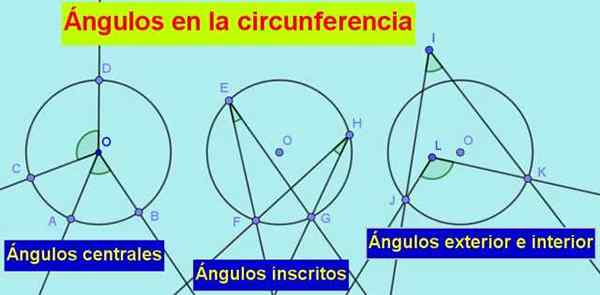
1.- Dia sudut tengah, yang simpulnya berada di tengah keliling dan sisi -sisinya mengering, seperti yang kita lihat pada gambar berikut:

Gambar 1. Jenis sudut di lingkar adalah: pusat, tertulis, eksterior dan interior. Sumber: f. Zapata.

2.- Dia sudut terdaftar, yang simpulnya ada di lingkar dan sisinya kering atau bersinggungan ke lingkar.

3.- Sudut luar, yang simpulnya keluar dari lingkar tetapi sisinya kering atau bersinggungan ke lingkar.

4.- Dia Sudut dalam, dengan simpul di dalam lingkar dan sisi keringnya bersamaan.

Semua sudut ini menjaga hubungan tertentu satu sama lain dan ini membawa kita ke sifat -sifat penting di antara sudut -sudut yang termasuk dalam lingkar yang diberikan.

[TOC]

Properti

- Sudut tengah

Sudut pusat didefinisikan sebagai orang yang simpulnya berada di tengah keliling dan sisi -sisinya dipotong ke lingkar.

Ukuran radianes dari sudut pusat adalah hasil bagi antara busur yang subtends, yaitu, keliling busur antara sisi sudut, dan jari -jari keliling keliling. 

Jika kelilingnya adalah kesatuan, yaitu jari -jari 1, maka ukuran sudut pusat adalah panjang busur, yang sesuai dengan jumlah radian.

Jika Anda ingin ukuran sudut tengah dalam derajat, maka ukurannya dikalikan dalam radian dengan faktor 180º/π.

Instrumen pengukuran sudut, seperti transporter dan goniometer, selalu menggunakan sudut pusat dan panjang busur subtense.

Dapat melayani Anda: turunan parsial: properti, perhitungan, latihan

Mereka dikalibrasi dalam derajat seksasimal, yang berarti bahwa setiap kali sudut diukur dengan mereka, di belakang yang diukur adalah panjang busur yang diganti dengan sudut pusat.

Properti

Ukuran sudut tengah dalam radianes sama dengan panjang busur yang subtin atau intersep dibagi dengan panjang radius.

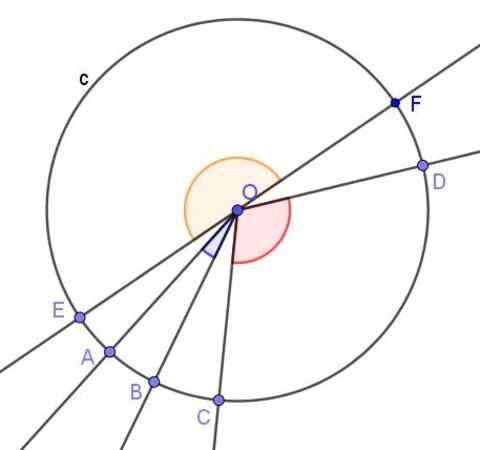Gambar 2. Tiga sudut tengah ditampilkan. Satu akut, yang lain tumpul dan satu datar. Sumber: f. Zapata.

- Sudut terdaftar

Sudut terdaftar dari lingkar adalah yang memiliki simpul di lingkar dan semi -jalannya kering atau bersinggungan. 

Propertinya adalah:

Properti

-Sudut terdaftar adalah cembung atau datar.

-Ketika sudut tertulis mencegat busur yang sama dengan sudut tengah, ukuran yang pertama akan menjadi setengah dari yang kedua.

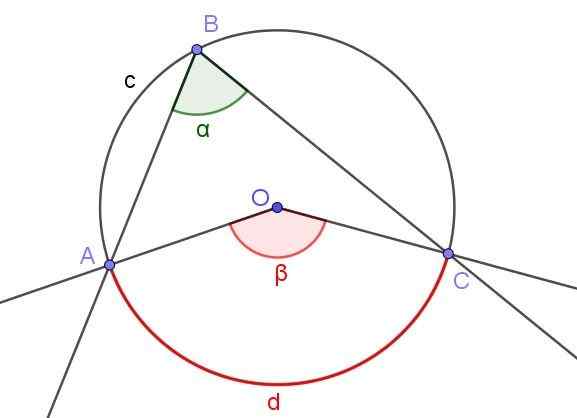Gambar 3. Sudut Terdaftar ∠ABC dan sudut pusat ∠AOC yang subtit ARC A⌒C yang sama. Sumber: f. Zapata.

Gambar 3 menunjukkan dua sudut ∠ABC dan ∠AOC yang mencegat keliling keliling yang sama.

Jika ukuran sudut terdaftar adalah α, maka ukuran β dari sudut pusat adalah dua kali ukuran sudut terdaftar (β = 2 α) karena keduanya mengurangi busur yang diukur yang sama.

- Sudut luar

Itu adalah sudut yang simpulnya berada di luar lingkar dan masing -masing sisi memotong ke lingkar di satu atau lebih titik.

Properti

-Ukurannya sama dengan semi -express (atau perbedaan dibagi dengan 2) dari sudut pusat yang mencegat lengkungan itu sendiri.

Untuk memastikan bahwa ukurannya positif, semi -express harus selalu menjadi sudut pusat dari ukuran terbesar kurang dari ukuran sudut tengah yang lebih rendah, seperti yang diilustrasikan dalam gambar berikut.

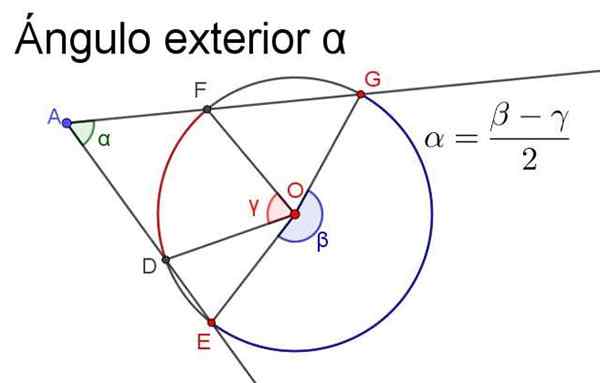Gambar 4. Sudut luar α sama dengan semi -referensi sentral yang menggantikan lengkungan yang sama. Sumber: f. Zapata.

- Sudut dalam

Sudut bagian dalam adalah orang yang simpulnya berada di dalam lingkar dan sisi -sisinya dipotong ke lingkar.

Dapat melayani Anda: koefisien penentuan: rumus, perhitungan, interpretasi, contoh

Properti 

Ukurannya sama dengan semi -soke sudut tengah yang menggantikan busur yang sama, ditambah sudut tengah yang menggantikan busur yang sama dengan sudut ekstensi (ini adalah sudut dalam yang dibentuk oleh komplementer semi -tegas dengan yang asli dari yang asli sudut dalam).

Gambar berikut menggambarkan dan mengklarifikasi properti dari sudut dalam.

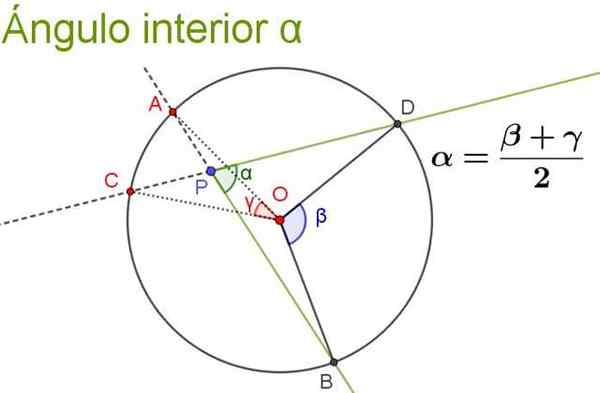Gambar 5. Sudut bagian dalam α sama dengan semi -seismum dari sudut tengah yang menempelkan lengkungan yang sama seperti dia sendiri. Sumber: f. Zapata.

Latihan terpecahkan

- Latihan 1

Misalkan sudut tertulis di mana salah satu sisinya melewati pusat keliling, seperti yang ditunjukkan pada Gambar 6. Jari -jari keliling adalah OA = 3 cm dan busur D memiliki panjang π/2 cm. Tentukan nilai sudut α dan β.

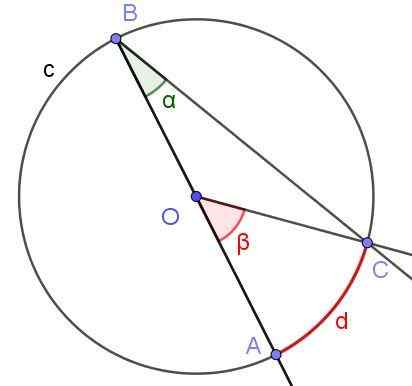Gambar 6. Sudut Terdaftar ∠ABC dengan sisi [BA) melalui O dan sudut tengah ∠AOC.Sumber: f. Zapata.

Larutan

Dalam hal ini, COB Isosceles Triange terbentuk, karena [OC] = [OB]. Dalam segitiga Isosceles, sudut yang berdekatan dengan pangkalan adalah sama, oleh karena itu mereka harus ∠BCO = ∠ABC = α. Di sisi lain ∠cob = 180º - β. Mempertimbangkan jumlah sudut internal segitiga Cob yang Anda miliki:

α + α + (180º - β) = 180º

Dari mana ia mengikuti bahwa 2 α = β, atau apa yang setara α = β/2, yang mengkonfirmasi properti (3) dari bagian sebelumnya, bahwa ukuran sudut terdaftar adalah setengah dari sudut pusat, ketika kedua sudutnya mengurangi tali yang sama [ac].

Sekarang kita melanjutkan untuk menentukan nilai numerik: sudut β adalah pusat dan ukurannya di Radianes adalah rasio antara arc d dan jari -jari r = oA, jadi ukurannya adalah:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Dapat melayani Anda: segi empat: elemen, properti, klasifikasi, contoh

Di sisi lain sudah ditegaskan bahwa α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Latihan 2

Pada Gambar 7 sudut α₁ dan β₂ memiliki ukuran yang sama. Selain sudut β₁ Ini mengukur 60º. Tentukan sudut β dan α.

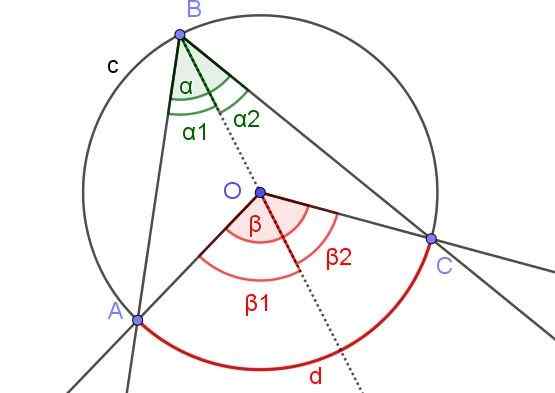Gambar 7. Pada gambar α₁ = β₂ dan β₁ = 60º. Tentukan nilai β dan α. Sumber: f. Zapata.

Larutan

Dalam hal ini ada sudut tertulis ∠ABC di mana pusat atau keliling berada di dalam sudut.

Karena properti (3) Anda memiliki α₂ = β₂ /2 dan α₁ = β₁ /2. Sebagai:

α = α₁ + α₂ dan β = β₁ + β₂

Karena itu Anda memiliki:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Yaitu, menurut properti:

α = β / 2

Seperti yang kita diberitahu bahwa β₁ = 60º Lalu:

α₁ = β₁ / 2 = 60º / 2 = 30º.

Mereka juga memberi tahu kami bahwa α₁ = β₂ Jadi itu mengikuti itu:

β₂ = 30º.

Sudut β adalah:

β₁ + β₂ = 60º + 30º = 90º.

Dan sebagai α = β / 2, lalu:

α = 90º / 2 = 45º. 

Kesimpulannya:

β = 90º dan α = 45º.

Referensi

1. Baldor, a. 1973. Geometri dan Trigonometri. Editorial Budaya Amerika Tengah.
2. DAN. KE. 2003. Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
3. Geometri 1. Sudut di lingkar. Pulih dari: edu.Xunta.adalah.
4. Semua sains. Menyelesaikan latihan sudut di lingkar. Pulih dari: francesphysics.Blogspot.com
5. Wikipedia. Sudut terdaftar. Pulih dari: is.Wikipedia.com