Penjelasan kondisi keseimbangan kedua, contoh, latihan

Itu Kondisi keseimbangan kedua Ini menetapkan bahwa jumlah torsi atau momen yang diproduksi oleh semua kekuatan yang bertindak pada tubuh, terlepas dari titik apa yang dihitung, harus dibatalkan sehingga tubuh tersebut berada dalam keseimbangan statis atau dinamis.

Menunjukkan torsi atau momen kekuatan melalui surat Yunani τ, Secara matematis itu dinyatakan sebagai berikut:

∑ τ = 0

Gambar 1. Untuk menyeimbangkan rocker, perlu menerapkan kondisi keseimbangan kedua. Sumber: Pxhere.

Surat tebal menunjukkan sifat vektor momen, yang harus dibatalkan sehubungan dengan titik mana pun yang dipilih sebagai pusat putaran. Dengan cara ini, membatalkan torsi bersih, dijamin bahwa objek tidak mulai berbalik atau berputar.

Namun, jika objek sudah berputar sebelumnya, dan torsi jaring tiba -tiba menghilang, rotasi akan berlanjut, tetapi dengan kecepatan sudut konstan.

Kondisi kesetimbangan kedua digunakan bersama dengan kondisi pertama, yang mengatakan bahwa jumlah kekuatan pada tubuh harus batal, sehingga tidak bergerak, atau jika itu terjadi, itu dengan gerakan bujursangkar yang seragam:

∑ F = 0

Kedua kondisi berlaku untuk tubuh yang diperluas, mereka yang dimensinya dapat diukur. Ketika suatu objek seharusnya menjadi partikel, tidak masuk akal untuk berbicara tentang rotasi, dan kondisi pertama untuk menjamin keseimbangan sudah cukup.

Contoh

Kondisi keseimbangan kedua terungkap dalam situasi yang tak terhitung jumlahnya:

Saat menaiki tangga

Saat menopang tangga di lantai dan dinding, kita perlu cukup untuk menggosok, terutama di lantai, untuk memastikan bahwa tangga tidak tergelincir. Jika kita mencoba memanjat tangga yang didukung di lantai yang berminyak, basah atau licin, tidak sulit untuk mengantisipasi bahwa kita akan jatuh.

Untuk dapat menggunakan tangga dengan penuh percaya.

Itu dapat melayani Anda: Pluto (planet kerdil)

Memindahkan lemari

Ketika Anda ingin memindahkan furnitur tinggi sebagai lemari, atau bagian mana pun yang tinggi lebih besar dari lebar, lebih mudah untuk mendorong pada titik rendah, untuk menghindari terbalik, dengan cara ini lebih mungkin bahwa furnitur akan meluncur sebagai gantinya berbalik dan berbaring.

Dalam keadaan seperti itu furnitur tidak harus dalam keseimbangan, karena dapat dipindahkan dengan cepat, tetapi setidaknya tidak akan berubah.

Balkon

Balkon yang unggul bangunan harus dibangun menjamin bahwa, meskipun ada banyak orang di atas, itu tidak berubah dan runtuh.

Dielektrik di medan listrik eksternal

Saat menempatkan bahan dielektrik di medan listrik eksternal, molekul bergerak dan berputar untuk mengadopsi posisi kesetimbangan, menciptakan medan listrik di dalam material.

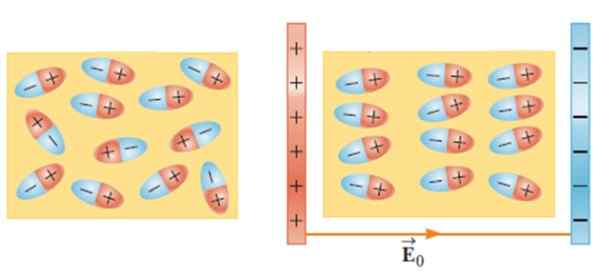Gambar 2.- Tanpa medan listrik eksternal, dipol secara acak (kiri). Bidang eksternal menerapkan torsi pada molekul dielektrik dan ini direorganisasi. Sumber: Serway, R. Fisika untuk Sains dan Teknik.

Efek ini membuat kapasitas kondensor meningkat ketika bahan seperti kaca, karet, kertas atau minyak diperkenalkan di antara baju besinya.

Tanda dan lampu

Adalah umum bagi banyak tempat untuk menggantung pemberitahuan di dinding bangunan, sehingga mereka terlihat oleh orang yang lewat.

Poster diikat dengan batang dan kabel, keduanya diperbaiki di dinding menggunakan dukungan. Berbagai kekuatan yang bertindak harus memastikan bahwa poster itu tidak jatuh, di mana kedua kondisi kesetimbangan mulai beraksi.

Reflektor di taman juga dapat ditempatkan dengan cara ini, seperti pada gambar berikut:

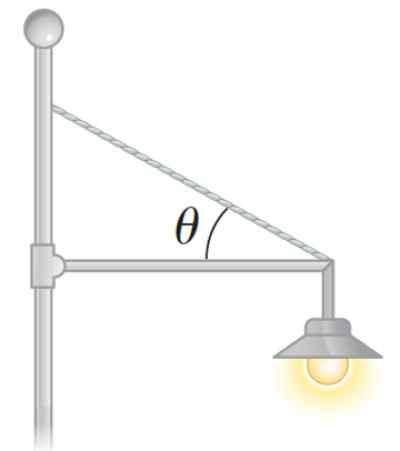Gambar 3. Lampu keseimbangan statis. Sumber: Serway. Fisika untuk Sains dan Teknik.

Cara menghitung torsi bersih atau momen bersih dari suatu gaya?

Torsi atau momen kekuatan, dilambangkan dengan τ salah satu M Dalam beberapa teks, selalu dihitung sehubungan dengan beberapa titik di mana sumbu rotasi melewati.

Itu didefinisikan sebagai produk vektor antara vektor posisi R, yang diarahkan dari sumbu tersebut ke titik penerapan kekuatan dan kekuatan F:

Dapat melayani Anda: Saldo Termodinamika: Kelas dan Aplikasi

τ = R × F

Menjadi vektor, perlu untuk mengekspresikan torsi yang memberikan besarnya, arah, dan maknanya. Besarnya diberikan oleh:

τ = rf.dosa θ

Aturan yang tepat untuk produk vektor

Saat masalah ada di pesawat, alamat torsi tegak lurus terhadap kertas atau layar dan arah ditentukan oleh aturan kanan, di mana indeks menunjuk ke arah R, Jari tengah menuju F Dan jempolnya memberi sinyal di dalam atau di luar kertas.

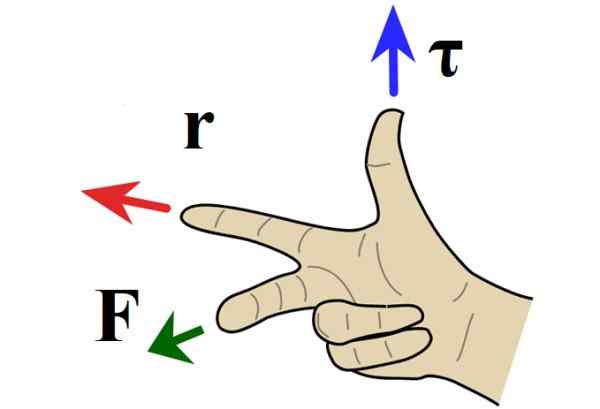Gambar 4. Aturan Tangan Kanan untuk Produk Vektor. Sumber: Wikimedia Commons.

Ketika torsi menunjuk keluar dari kertas, rotasi berada di arah yang berlawanan dengan jarum jam dan diberi tanda positif berdasarkan konvensi. Jika sebaliknya torsi diarahkan dalam lembaran, rotasi berada di arah tangan dan tanda negatif.

Untuk menemukan torsi bersih, titik yang nyaman untuk perhitungan dipilih, yang bisa menjadi yang di mana jumlah kekuatan terbesar bertindak. Dalam hal ini momen kekuatan ini batal, untuk memiliki vektor posisi R Besarnya 0.

Anda dapat memilih titik apa pun yang menawarkan informasi yang cukup untuk menghapus hal yang tidak diketahui yang meminta masalah untuk diselesaikan. Mari kita lihat lebih detail.

Olahraga diselesaikan

Reflektor gambar berikut memiliki 20 kg massa dan didukung oleh bar tipis horizontal, dari massa dan panjang tercela, yang diartikulasikan ke pos. Kabel, juga cahaya, yang membantu mempertahankan reflektor membentuk sudut θ = 30 º dengan batang. Menghitung:

a) Ketegangan di kabel

b) Besarnya gaya f yang diterapkan pada batang melalui engsel.

Larutan

Kami akan menerapkan kondisi keseimbangan pertama ∑ F = 0 ke gaya yang ditunjukkan dalam diagram:

Dapat melayani Anda: panas yang diserap: formula, cara menghitungnya dan menyelesaikan latihan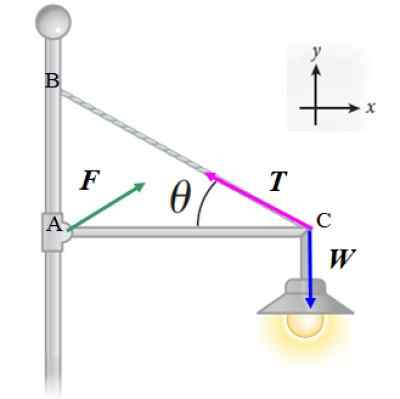

F + T + W = 0

Perhatikan bahwa besarnya dan arah F Mereka belum ditentukan, tetapi kami berasumsi bahwa ia memiliki dua komponen: f_X dan f_Dan. Dengan cara ini kita mendapatkan dua persamaan:

F_X -T. cos θ = 0

F_Dan - W + t⋅ sin θ = 0

Sekarang mari kita terapkan kondisi keseimbangan kedua, memilih titik A, karena kita tidak tahu besarnya F juga tidak T. Saat memilih poin ini, vektor R_KE batal, oleh karena itu momen F batal dan besarnya F Itu tidak akan muncul dalam persamaan:

-W⋅l + T⋅sen θ⋅l = 0

Karena itu:

T.dosa θ.L = w.L

T = w/sen θ = (20 kg x 9.8 m/s²) / Dosa 30 º = 392 n

Mengetahui besarnya T kita dapat menghapus komponen f_X:

F_X = T⋅ cos θ = 392 cos 30º N = 339. 5 n

Dan kemudian komponen f_Dan:

F_Dan = W - t⋅ sin θ = (20 kg x 9.8 m/s²) - 392⋅sen 30 º = 0

Lalu kita bisa mengekspresikan F Jadi:

F = 339.5 n X

Karena itu merupakan kekuatan horizontal. Ini karena kami menganggap bahwa bar memiliki bobot tercela.

Jika titik C telah dipilih untuk menghitung momen yang dihasilkan, vektor R_T Dan R_W Mereka nol, oleh karena itu:

M = f_Y⋅L = 0

Disimpulkan bahwa f_Dan = 0. Dengan demikian:

- W + t⋅ sin θ = 0

T = w/ sin θ

Yang merupakan hasil yang sama awalnya diperoleh dengan memilih titik A sebagai situs tempat sumbu rotasi lewat.

Tema yang menarik

Kondisi keseimbangan.

Kondisi saldo pertama.

Referensi

1. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley.
2. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 4. Sistem partikel. Diedit oleh Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.
5. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage.