Sudut tambahan yaitu, perhitungan, contoh, latihan

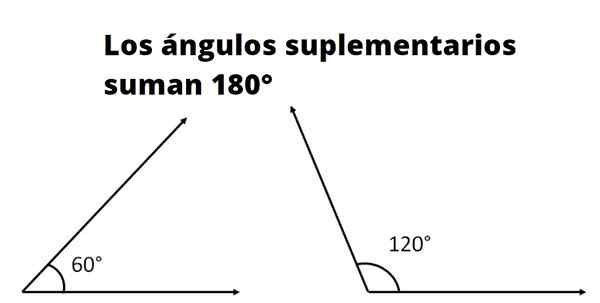
Dua atau lebih sudut tambahan Jika jumlah tindakannya sesuai dengan ukuran sudut datar. Ukuran sudut datar, juga disebut sudut datar, dalam derajat adalah 180º dan di Radianes adalah π.

Sebagai contoh, kami menemukan bahwa tiga sudut interior dari segitiga adalah tambahan, karena jumlah langkahnya adalah 180º. Tiga sudut ditunjukkan pada Gambar 1. Dari atas, ia mengikuti bahwa α dan β adalah pelengkap, karena mereka berdekatan dan jumlah penuhnya sudut datar.

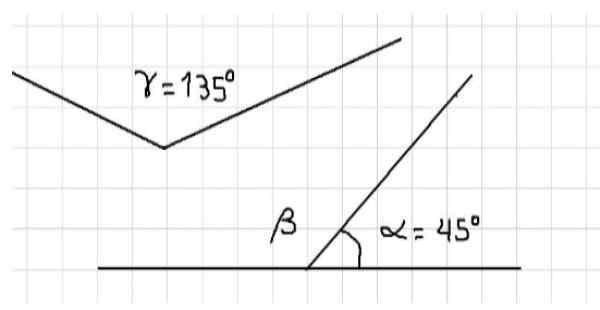
Gambar 1: α dan β adalah pelengkap. α dan γ adalah tambahan. Sumber: f. Zapata.

Juga pada gambar yang sama, ada sudut α dan γ yang juga merupakan pelengkap, karena jumlah tindakan mereka sama dengan tingkat sudut datar, yaitu, 180º. Tidak dapat dikatakan bahwa sudut β dan γ bersifat tambahan karena keduanya bersikap tumpul, langkah -langkah mereka lebih besar dari 90º dan oleh karena itu jumlahnya melebihi 180º.

Sumber: Lafer.com

Di sisi lain, dapat dikatakan bahwa ukuran sudut β sama dengan ukuran sudut γ, karena jika β adalah tambahan α dan γ adalah tambahan α, maka β = γ = 135º.

[TOC]

Contoh

Dalam contoh -contoh berikut ini diminta untuk menemukan sudut yang tidak diketahui, ditunjukkan dengan interogasi pada Gambar 2. Mereka berkisar dari contoh paling sederhana hingga sedikit lebih rumit daripada pembaca yang harus lebih berhati -hati.

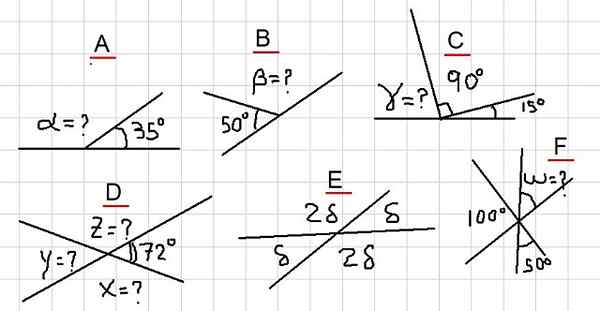Gambar 2. Berbagai contoh sudut tambahan. Sumber: f. Zapata.

Contoh a

Pada gambar kita memiliki sudut yang berdekatan α dan 35º Tambahkan sudut datar. Yaitu, α + 35º = 180º dan karenanya terpenuhi bahwa: α = 180º- 35º = 145º.

Contoh b

Karena β adalah pelengkap dengan sudut 50º, maka diikuti β = 180º - 50º = 130º.

Dapat melayani Anda: apa elemen perumpamaan? (Bagian)

Contoh c

Dari Gambar 2C Jumlah berikut diperhatikan: γ + 90º + 15º = 180º. Yaitu, γ adalah pelengkap dengan sudut 105º = 90º + 15º. Disimpulkan bahwa itu: 

γ = 180º- 105º = 75º

Contoh d

Karena x adalah pelengkap dengan 72º, maka x = 180º - 72º = 108º. Selain itu dan pelengkap dengan x, lalu y = 180º - 108º = 72º.

Dan akhirnya z adalah tambahan dengan 72º, oleh karena itu z = 180º - 72º = 108º.

Contoh e

Sudut δ dan 2Δ adalah tambahan, oleh karena itu Δ + 2Δ = 180º. Yang berarti bahwa 3Δ = 180º, dan ini pada gilirannya memungkinkan penulisan: δ = 180º / 3 = 60º.

Contoh f

Jika kita menyebut sudut antara 100º dan 50º, maka perlu ditambah dengan mereka, karena diamati bahwa jumlah penuh mereka adalah sudut datar mereka.

Ini mengikuti bahwa u = 150º. Sebagai u ditentang oleh simpul ke w, maka w = u = 150º.

Latihan

Tiga latihan diusulkan di bawah ini, dalam semua dari mereka nilai sudut A dan B harus ditemukan dalam derajat, sehingga hubungan yang ditunjukkan pada Gambar 3 terpenuhi. Konsep sudut tambahan digunakan dalam resolusi semuanya.

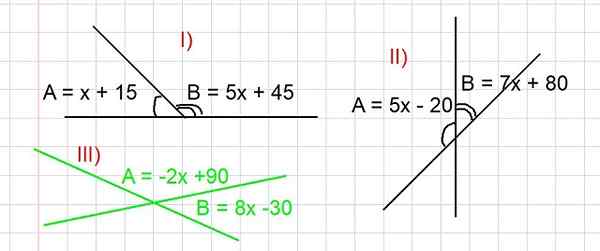Gambar 3. Angka untuk menyelesaikan Latihan I, II dan III pada sudut tambahan. Semua sudut diekspresikan dalam derajat. Sumber: f. Zapata.

- Latihan I

Tentukan nilai sudut A dan B dari Bagian I) dari Gambar 3.

Larutan

A dan B adalah tambahan, di mana A + B = 180 derajat harus diganti, maka ekspresi A dan B diganti sebagai fungsi x, seperti yang muncul pada gambar:

(x + 15) + (5x + 45) = 180

Persamaan linear orde pertama diperoleh. Untuk menyelesaikannya, istilah dibuang: istilah:

6 x + 60 = 180

Dapat melayani Anda: bilangan real: riwayat, contoh, properti, operasi

Membagi kedua anggota antara 6 adalah:

x + 10 = 30

Dan akhirnya membersihkan, maka x bernilai 20º.

Sekarang nilai x harus diganti untuk menemukan sudut yang dipesan. Dari sana Anda harus sudut A adalah: A = 20 +15 = 35º.

Dan untuk bagiannya, sudut B adalah B = 5*20 + 45 = 145º.

- Latihan II

Temukan nilai sudut A dan B dari Bagian II) dari Gambar 3.

Larutan

Sebagai A dan B adalah sudut tambahan, A + B = 180 derajat memiliki. Mengganti ekspresi A dan B sebagai fungsi x yang diberikan pada Bagian II) dari Gambar 3 adalah:

(-2x + 90) + (8x - 30) = 180

Sekali lagi persamaan tingkat pertama diperoleh, yang persyaratannya harus dikelompokkan dengan mudah:

6 x + 60 = 180

Membagi kedua anggota antara 6 adalah:

x + 10 = 30

Di mana ia bernilai 20º.

Artinya sudut A = -2*20 + 90 = 50 °. Sedangkan sudut b = 8*20-30 = 130.

- Latihan III

Tentukan nilai sudut A dan B dari Bagian III) dari Gambar 3 (berwarna hijau).

Larutan

Sebagai A dan B adalah sudut tambahan, A + B = 180 derajat memiliki. Ekspresi A dan B harus diganti sebagai fungsi x yang diberikan pada Gambar 3, yang Anda miliki:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Membagi kedua anggota dengan 12 untuk menghapus nilai X, Anda memiliki:

x + 5 = 15

Akhirnya ditemukan bahwa X bernilai 10 derajat.

Sekarang lanjutkan untuk mengganti untuk menemukan sudut A: A = 5*10 -20 = 30 °. Dan untuk sudut b: b = 7*10 + 80 = 150º

Dapat melayani Anda: apa rentang statistiknya? (Dengan contoh)

Sudut tambahan dalam dua paralel dipotong oleh sekte

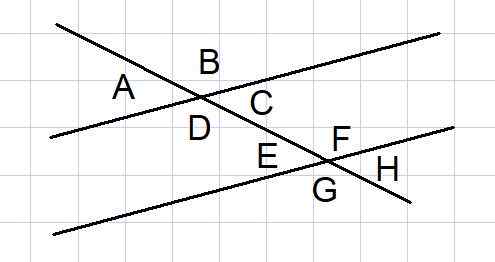Gambar 4. Sudut antara dua paralel dipotong oleh sekte. Sumber: f. Zapata.

Dua garis paralel dipotong oleh sekte adalah konstruksi geometris yang biasa dalam beberapa masalah. Di antara baris seperti itu, 8 sudut terbentuk seperti yang ditunjukkan pada Gambar 4.

Dari 8 sudut itu, beberapa pasangan sudut adalah pelengkap, yang kami daftarkan di bawah ini:

1. Sudut eksternal ke dan B, dan eksterior g dan h
2. Sudut interior d dan c, dan interior e dan f
3. Sudut eksternal a dan g, dan b dan h eksternal
4. Sudut internal d dan e, dan narapidana c dan f

Dengan kelengkapan, sudut yang sama juga dinamai:

1. Pergantian internal: D = F dan C = E
2. Pergantian eksternal: a = h dan b = g
3. Yang sesuai: a = e dan c = h
4. Lawan oleh vertex a = c dan e = h
5. Yang sesuai: b = f dan d = g
6. Lawan oleh vertex b = d dan f = g

- Latihan IV

Mengacu pada Gambar 4, di mana sudut menunjukkan antara dua garis paralel dipotong oleh sekte, tentukan nilai semua sudut dalam radian, mengetahui bahwa sudut A = π/6 radian.

Larutan

A dan B adalah sudut eksternal tambahan karena itu b = π - a = π - π/6 = 5π/6

A = E = C = H = π/6

B = f = d = g = 5π/6

Referensi

1. Baldor, j. KE. 1973.Geometri datar dan ruang. Budaya Amerika Tengah. 
2. Hukum dan Rumus Matematika. Sistem Pengukuran Sudut. Diperoleh dari: ingemecanica.com.
3. Wentworth, g. Geometri planet. Pulih dari: Gutenberg.org.
4. Wikipedia. Sudut tambahan. Pulih dari: is.Wikipedia.com
5. Wikipedia. Konveyor. Pulih dari: is.Wikipedia.com
6. Zapata f. Goniometer: Sejarah, Bagian, Operasi. Diperoleh dari: Lifer.com