Sejarah Bilangan Irasional, Properti, Klasifikasi, Contoh

Itu bilangan irasional Mereka adalah mereka yang ekspresi desimal memiliki angka tak terbatas tanpa pola berulang, oleh karena itu, mereka tidak dapat diperoleh dengan membuat hasil bagi antara dua bilangan bulat.

Di antara bilangan irasional yang paling terkenal adalah:

Gambar 1. Dari atas ke bawah bilangan irasional berikut: pi, jumlah euler, aúrea dan dua akar persegi. Sumber: Pixabay.

Di antara mereka, tanpa keraguan π (pi) adalah yang paling akrab, tetapi ada banyak lagi. Semuanya termasuk dalam set bilangan real, yang merupakan himpunan numerik yang menyatukan bilangan rasional dan irasional.

Poin suspensi pada Gambar 1 menunjukkan bahwa desimal mengikuti tanpa batas waktu, yang terjadi adalah bahwa ruang kalkulator saat ini hanya memungkinkan untuk menunjukkan beberapa.

Jika kita melihat dengan cermat, asalkan kita membuat hasil bagi antara dua bilangan bulat, desimal dengan angka terbatas diperoleh atau jika tidak, dengan angka tak terbatas di mana satu atau lebih mereka diulangi. Nah, ini tidak terjadi dengan bilangan irasional.

[TOC]

Sejarah bilangan irasional

Ahli matematika hebat Pythagoras kuno, lahir pada tahun 582.C di Samos, Yunani, mendirikan sekolah pemikiran Pythagoras dan menemukan teorema terkenal yang menyandang namanya. Kami membawanya ke kiri (orang Babilonia sudah bisa mengenalnya jauh sebelumnya).

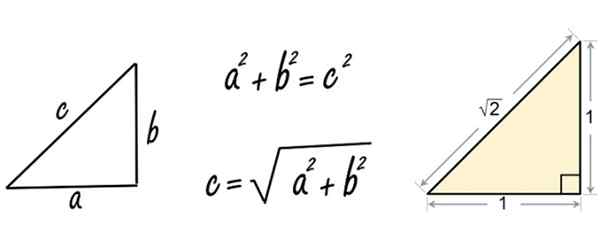Gambar 2. Teorema Pythagoras diterapkan pada segitiga sisi sama dengan 1. Sumber: Pixabay/Wikimedia Commons.

Nah, ketika Pythagoras (atau mungkin muridnya) menerapkan teorema pada segitiga kanan sisi yang sama dengan 1, menemukan bilangan irasional √2.

Itu bisa melayani Anda: garis pengeringan

Dia melakukannya dengan cara ini:

C = √1² + 1² = √1+1 = √2

Dan dia segera menyadari bahwa angka baru ini tidak berasal dari hasil bagi antara dua bilangan alami lainnya, yang diketahui pada waktu itu.

Karena itu dia memanggilnya irasional, Dan penemuan itu menyebabkan kecemasan dan kebingungan besar di antara orang Pythagoras.

Sifat bilangan irasional

-Himpunan semua bilangan irasional dilambangkan dengan huruf I dan kadang -kadang seperti q* atau q^C. Persatuan antara bilangan irasional I atau Q* dan bilangan rasional Q, memunculkan himpunan angka N nyata.

-Dengan bilangan irasional, operasi aritmatika yang diketahui dapat dilakukan: jumlah, pengurangan, perkalian, pembagian, potensiasi dan banyak lagi.

-Pembagian antara 0 tidak didefinisikan di antara bilangan irasional.

-Jumlah dan produk antara bilangan irasional belum tentu bilangan irasional lain. Misalnya:

√2 x √8 = √16 = 4

Dan 4 bukan bilangan irasional.

-Namun, jumlah bilangan rasional ditambah yang tidak rasional menghasilkan irasional. Cara ini:

1 + √2 = 2.41421356237…

-Produk dari bilangan rasional yang berbeda dari 0 dengan bilangan irasional juga tidak rasional. Mari kita lihat contoh ini:

2 x √2 = 2.828427125…

-Kebalikan dari hasil irasional dalam bilangan irasional lain. Mari kita coba beberapa:

1 / √2 = 0.707106781…

1 / √3 = 0.577350269…

Angka -angka ini menarik karena mereka juga merupakan nilai -nilai dari beberapa alasan trigonometri sudut yang diketahui. Banyak alasan trigonometri adalah bilangan irasional, tetapi ada pengecualian, seperti sen 30º = 0.5 = ½, yang rasional.

-Dalam jumlah tersebut, sifat komutatif dan asosiatif terpenuhi. Jika A dan B adalah dua bilangan irasional, ini berarti bahwa:

Dapat melayani Anda: Fungsi Overjektif: Definisi, Properti, Contoh

A + b = b + a.

Dan jika C adalah bilangan irasional lain, maka:

(A + b) + c = a + (b + c).

-Properti distributif perkalian sehubungan dengan jumlah adalah properti lain yang diketahui yang juga dipenuhi untuk bilangan irasional. Pada kasus ini:

ke.(b+c) = a.b + a.C.

-Irasional untuk memiliki kebalikannya: -a. Saat hasilnya ditambahkan, itu adalah 0:

A+(-a) = 0

-Di antara dua yang rasional yang berbeda, setidaknya ada satu bilangan irasional.

Lokasi bilangan irasional di garis nyata

Garis nyata adalah garis horizontal di mana bilangan real berada, di mana irasionalnya adalah bagian penting.

Untuk menemukan bilangan irasional di garis nyata, dalam bentuk geometris, kita bisa sepadan dengan teorema Pythagoras, aturan dan kompas.

Sebagai contoh, kita akan menemukan √5 di garis nyata, di mana kita menggambar segitiga persegi panjang sisi x = 2 Dan y = 1, Seperti yang ditunjukkan gambar:

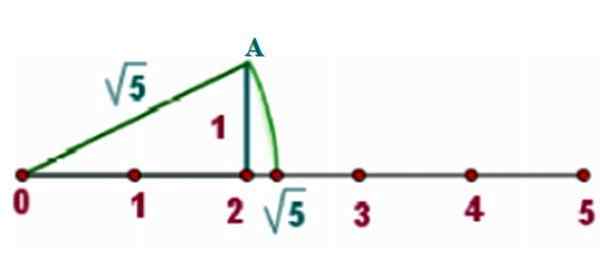Gambar 3. Metode untuk menemukan bilangan irasional di garis nyata. Sumber: f. Zapata.

Untuk teorema Pythagoras, hipotenus dari segitiga seperti itu adalah:

C = √2² + 1² = √4+1 = √5

Sekarang ketukan dengan ujung ditempatkan di 0, di mana ada juga salah satu simpul segitiga siku. Ujung pensil kompas harus di titik.

Busur keliling ditarik yang memotong garis asli. Karena jarak antara pusat keliling dan titik apa pun yang sama adalah jari -jari, yang bernilai √5, titik persimpangan juga √5 dari pusat.

Dari grafik terlihat bahwa √5 adalah antara 2 dan 2.5. Kalkulator menawarkan nilai perkiraan dari:

Dapat melayani Anda: koefisien penentuan: rumus, perhitungan, interpretasi, contoh

√5 = 2.236068

Maka, membangun segitiga dengan sisi yang sesuai, yang tidak rasional lainnya dapat ditemukan, seperti √7 dan lainnya.

Klasifikasi bilangan irasional

Bilangan irasional diklasifikasikan menjadi dua kelompok:

-Aljabar

-Transenden atau transendental

Angka aljabar

Angka aljabar, yang bisa irasional atau tidak, adalah solusi dari persamaan polinomial yang bentuk umumnya adalah:

ke_N X^N + ke_N-1X^N-1 + ke_N-2X^N-2 +.. . +ke₁x + a_{salah satu} = 0

Contoh persamaan polinomial adalah persamaan tingkat kedua seperti ini:

X³ - 2x = 0

Mudah untuk menunjukkan bahwa bilangan irasional √2 adalah salah satu solusi dari persamaan ini.

Angka transenden

Sebaliknya, angka transenden, meskipun irasional, tidak pernah muncul sebagai solusi dari persamaan polinomial.

Angka transenden yang paling sering ditemukan dalam matematika yang diterapkan adalah π, untuk hubungannya dengan keliling dan angka E, atau angka Euler, yang merupakan dasar dari logaritma Neperian.

Latihan

Di kotak hitam abu -abu ditempatkan pada posisi yang ditunjukkan pada gambar. Diketahui bahwa permukaan kuadrat hitam adalah 64 cm². Berapa panjang kedua kotak?

Gambar 4. Dua kotak, di mana panjang sisi dapat ditemukan. Sumber: f. Zapata.

Menjawab

Permukaan persegi sisi L adalah:

A = l²

Karena kotak hitam adalah 64 cm² Area, sisinya harus 8 cm.

Ukuran ini sama dengan Diagonal dari kotak abu -abu. Menerapkan teorema Pythagoras untuk diagonal ini, dan mengingat bahwa sisi -sisi dari ukuran persegi yang sama, kita akan memiliki:

8² = L_G² + L_G²

Dimana l_G Itu adalah sisi kotak abu -abu.

Oleh karena itu: 2l_G² = 8²

Menerapkan akar kuadrat di kedua sisi kesetaraan:

L_G = (8/√2) cm

Referensi

1. Carena, m. 2019. Manual Matematika Preuniversity. Universitas Nasional Pantai.
2. Figuera, J. 2000. Matematika ke -9. Derajat. Edisi Co-Bo.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Portal Pendidikan. Bilangan irasional dan propertinya. Diperoleh dari: PortalEducative.bersih.
5. Wikipedia. Bilangan irasional. Pulih dari: is.Wikipedia.org.