Fitur Gelombang Senoidal, Suku Cadang, Perhitungan, Contoh

Itu gelombang sinus Mereka adalah pola gelombang yang secara matematis dapat dijelaskan oleh fungsi sinus dan kosinus. Mereka dengan tepat menggambarkan peristiwa alam dan tanda -tanda variabel dalam waktu, seperti tegangan yang dihasilkan oleh pembangkit listrik dan kemudian digunakan di rumah, industri, dan jalanan.

Elemen listrik seperti resistensi, kapasitor dan induktansi, yang terhubung ke input tegangan sinusoidal, juga menghasilkan jawaban juga sinusoidal. Matematika yang digunakan dalam deskripsi mereka relatif sederhana dan telah dipelajari secara menyeluruh.

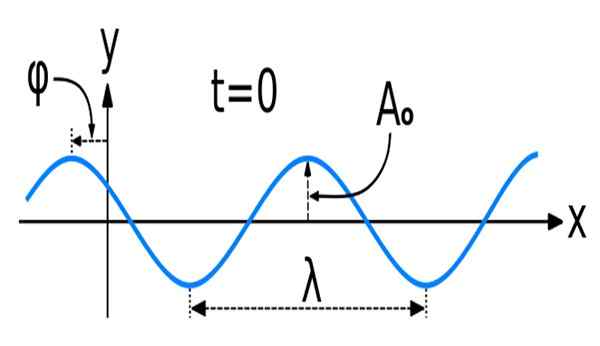
Gambar 1. Gelombang sinus dengan beberapa karakteristik spasial utamanya: amplitudo, panjang gelombang dan fase. Sumber: Wikimedia Commons. WAVE_NEW_SINE.SVG: Kraaiennestoriginal dibuat sebagai gelombang cosinus, oleh pengguna: peleg, sebagai file: wave_new.Pekerjaan SVGDERIVATIF: Dave3457 [CC BY-SA 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)]

Matematika gelombang sinusoidal atau sinusoidal, seperti yang diketahui, adalah fungsi sinus dan kosinus.

Ini adalah fungsi berulang, yang berarti periodisitas. Keduanya memiliki cara yang sama, dengan ketentuan bahwa cosinus dipindahkan ke kiri sehubungan dengan payudara di ruang siklus. Itu diamati pada Gambar 2:

Gambar 2. Fungsi Sen X dan Cos X dipindahkan satu sehubungan dengan yang lain. Sumber: f. Zapata.

Kemudian cos x = sin (x + π/2). Dengan bantuan fungsi -fungsi ini, gelombang sinus diwakili. Untuk melakukan ini, besarnya dipertanyakan ditempatkan pada sumbu vertikal, sedangkan di sumbu horizontal waktu terletak.

Kualitas berulang dari fungsi -fungsi ini juga dihargai pada grafik di atas: polanya diulang secara terus menerus dan secara teratur. Berkat fungsi -fungsi ini, Anda dapat mengekspresikan tegangan dan arus tipe Sinian yang bervariasi dari waktu ke waktu, menempatkan pada sumbu vertikal alih -alih Dan, A v atau satu yo untuk mewakili tegangan atau arus, dan pada sumbu horizontal alih -alih X, Itu T cuaca.

Cara paling umum untuk mengekspresikan gelombang sinus adalah:

v (t) = v_M dosa (Ωt+φ)

Maka kita akan memperdalam makna ekspresi ini, mendefinisikan beberapa istilah dasar untuk mengkarakterisasi gelombang sinus.

[TOC]

Para Pihak

Periode, amplitudo, frekuensi, siklus dan fase adalah konsep yang berlaku untuk gelombang periodik atau berulang dan penting untuk mengkarakterisasi dengan benar.

Periode

Fungsi periodik seperti yang disebutkan, yang diulang secara berkala, selalu memenuhi properti berikut:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) = .. .

Di mana T Itu adalah jumlah yang disebut melambai, Dan inilah waktu yang diperlukan untuk mengulangi fase yang sama. Dalam unit sistem internasional, periode diukur dalam hitungan detik.

Amplitudo

Menurut ekspresi umum gelombang Senoidal v (t) = v_M sin (ωt+φ), v_M Itu adalah nilai maksimum fungsi, yang terjadi saat sin (ωt+φ) = 1 (Mengingat bahwa nilai terbesar yang diakui oleh fungsi sinus dan kosinus keduanya adalah 1). Nilai maksimum ini justru Amplitudo Gelombang, juga dikenal sebagai amplitudo puncak.

Dalam hal tegangan akan diukur dalam volt dan jika arus akan ada di amp. Dalam gelombang sinus luasnya konstan, tetapi dalam jenis gelombang lain amplitudo dapat bervariasi.

Dapat melayani Anda: resistance thermometer: karakteristik, operasi, penggunaan

Siklus

Itu adalah bagian dari gelombang yang terkandung dalam suatu periode. Pada gambar sebelumnya periode diambil dengan mengukurnya dari dua puncak atau punggung berturut -turut, tetapi dapat mulai diukur dari bagian lain gelombang, sementara mereka dibatasi oleh suatu periode.

Catatan pada gambar berikut karena satu siklus mencakup dari satu titik ke titik lain dengan nilai (tinggi) yang sama dan kemiringan yang sama (kecenderungan).

Gambar 3. Dalam gelombang sinus, siklus selalu terjadi untuk suatu periode. Yang penting adalah titik awal dan ujungnya pada ketinggian yang sama. Sumber: Boylestad. Pengantar Analisis Sirkuit. Pearson.

Frekuensi

Jumlah siklus yang terjadi dalam 1 detik dan terkait dengan argumen fungsi sinus: ωt. Frekuensi dilambangkan sebagai F Dan diukur dalam siklus per detik atau hertz (Hz) dalam sistem internasional.

Frekuensinya adalah jumlah sebaliknya dari periode tersebut, oleh karena itu:

F = 1/t

Sementara frekuensi F terkait dengan Frekuensi sudut Ω (pulsasi) sebagai:

Ω = 2πF

Frekuensi sudut diekspresikan dalam radianes /detik dalam sistem internasional, tetapi radian tidak dimensi, sehingga frekuensinya F dan frekuensi sudut Ω Mereka memiliki dimensi yang sama. Perhatikan bahwa produk tersebut ωt memberikan radian sebagai hasilnya, dan harus diperhitungkan saat menggunakan kalkulator untuk mendapatkan nilai SEN ωt.

Fase

Ini sesuai dengan perpindahan horizontal yang dialami oleh gelombang, sehubungan dengan waktu yang diambil sebagai referensi.

Pada gambar berikut, gelombang hijau maju sehubungan dengan merah dalam satu waktu T_D. Dua gelombang sinusoidal masuk fase Saat frekuensi dan fase Anda sama. Jika fase berbeda, maka mereka masuk celah. Gambar 2 Gelombang juga sudah ketinggalan zaman.

Gambar 4. Gelombang sinusidal yang dilarut. Sumber: Wikimedia Commons. Tidak ada penulis yang dapat dibaca mesin. Kanjo ~ Commonswiki Diasumsikan (berdasarkan klaim hak cipta). [Area publik].

Jika frekuensi gelombang berbeda, mereka akan berada dalam fase saat fase ωt+φ Jadilah sama di kedua gelombang pada saat -saat tertentu.

Generator Gelombang Senoidal

Ada banyak cara untuk mendapatkan sinyal berbentuk sinus. Runnings buatan sendiri memberi mereka.

Penerapan Hukum Faraday

Cara yang cukup sederhana untuk mendapatkan sinyal sinus adalah dengan menggunakan hukum Faraday. Ini menunjukkan bahwa dalam sirkuit tertutup arus, misalnya loop, ditempatkan di tengah medan magnet, arus yang diinduksi dihasilkan ketika aliran medan magnet melalui itu berubah dari waktu ke waktu. Akibatnya, a Tegangan yang diinduksi salah satu diinduksi fem.

Aliran medan magnet bervariasi jika loop diputar dengan kecepatan sudut konstan di tengah medan yang dibuat antara kutub N dan S dari magnet yang ditunjukkan pada gambar.

Dapat melayani Anda: Neptunus (planet)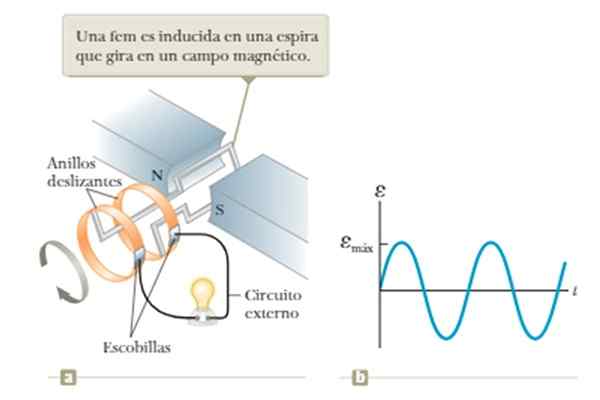Gambar 5. Generator Gelombang Berdasarkan Hukum Induksi Faraday. Sumber: Sumber: Raymond A. Serway, Jonh W. Jewett [CC BY-SA 4.0 (https: // createveCommons.Org/lisensi/by-sa/4.0)].

Keterbatasan operasi ini adalah ketergantungan pada tegangan yang diperoleh dengan frekuensi rotasi loop, seperti yang akan dilihat secara lebih rinci dalam Contoh 1 dari bagian contoh nanti.

Wien Oscillator

Cara lain untuk mendapatkan gelombang sinus, kali ini dengan elektron. Dengan cara ini, gelombang sinus diperoleh dengan frekuensi dan amplitudo yang dapat dimodifikasi pengguna sesuai dengan kenyamanan mereka, dengan cara penyesuaian sakelar.

Gambar tersebut menunjukkan generator sinyal sinus, dengan mana bentuk gelombang lain juga dapat diperoleh: segitiga dan kuadrat antara lain.

Gambar 6. Generator sinyal. Sumber: Sumber: Wikimedia Commons. Opgreg di Wikipedia Inggris [CC BY-SA 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)].

Cara menghitung gelombang sinus?

Untuk melakukan perhitungan yang melibatkan gelombang sinus, kalkulator ilmiah digunakan yang memiliki fungsi trigonometri sinus dan cosinus, serta kebalikannya. Kalkulator ini memiliki mode untuk mengerjakan sudut baik dalam derajat atau radiane, dan mudah untuk mengonversi satu cara ke yang lain. Faktor konversi adalah:

180 º = π Radianes.

Menurut model kalkulator, Anda harus menavigasi melalui tombol mode untuk menemukan opsi derajat, yang memungkinkan Anda bekerja pada fungsi trigonometri dalam derajat, atau opsi RAD, untuk secara langsung bekerja pada sudut di Radianes.

Misalnya sin 25 º = 0.4226 dengan kalkulator dimasukkan ke dalam mode DEG. Dengan mengonversi 25 º ke Radianes Anda mendapatkan 0.4363 Radianes dan sen 0.4363 rad = 0.425889 ≈ 0.4226.

Osiloskop

Osiloskop adalah peralatan yang memungkinkan untuk memvisualisasikan tanda -tanda layar tegangan dan arus baik alternatif dan langsung. Ini memiliki tombol untuk menyesuaikan ukuran sinyal pada kisi seperti yang ditunjukkan pada gambar berikut:

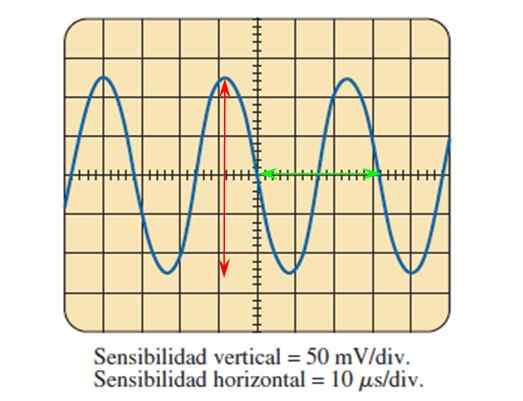Gambar 7. Sinyal sinusoidal diukur dengan osiloskop. Sumber: Boylestad.

Melalui gambar yang disediakan oleh osiloskop dan mengetahui penyesuaian sensitivitas di kedua sumbu, dimungkinkan untuk menghitung parameter gelombang yang dijelaskan di atas.

Dapat melayani Anda: galaksi elips: pembentukan, karakteristik, jenis, contoh

Gambar tersebut menunjukkan sinyal tegangan sinus sebagai fungsi waktu, di mana setiap pembagian sumbu vertikal bernilai 50 milivolt, sedangkan di sumbu horizontal, setiap divisi bernilai 10 mikrodetik.

Amplitudo puncak ke puncak adalah menghitung divisi yang meliputi gelombang secara vertikal, membantu panah merah:

5 Divisi dihitung dengan bantuan panah merah, sehingga tegangan puncak-pico adalah:

V_pp = 5 Divisi x 50 mV/Divisi = 250 mV.

Tegangan Pico V_P Diukur dari sumbu horizontal, menjadi 125 mV.

Untuk menemukan periode siklus diukur, misalnya yang dibatasi oleh panah hijau, yang mencakup 3.2 Divisi, maka periodenya adalah:

T = 3.2 Divisi x 10 mikrodetik/divisi = 32 mikrodetik = 32 μs

Contoh

Contoh 1

Untuk generator pada Gambar 3, tunjukkan dari hukum Faraday bahwa tegangan yang diinduksi memiliki sinus. Asumsikan bahwa loop terdiri dari belokan N, bukan satu, semua dengan area yang sama A dan berputar dengan kecepatan sudut konstan Ω di tengah medan magnet B seragam.

Larutan

Hukum Faraday mengatakan bahwa fem yang diinduksi ε adalah:

ε = -n (dφ_B /dt)

Di mana Φ_B Itu adalah aliran medan magnet, yang akan bervariasi, karena tergantung pada bagaimana loop terpapar ke bidang setiap saat. Tanda negatif hanya menggambarkan fakta bahwa FEM ini menentang penyebab yang menghasilkannya (hukum Lenz). Aliran karena satu loop adalah:

Φ_B = B.KE.cos θ

θ adalah sudut yang vektor normal ke bidang loop terbentuk dengan bidang B Saat rotasi terjadi (lihat gambar), sudut ini secara alami bervariasi sebagai:

θ = ωt

Sehingga: Φ_B = B.KE.cos θ = b.KE.cos ωt. Sekarang Anda hanya perlu memperoleh ekspresi ini sehubungan dengan waktu dan dengan itu FEM yang diinduksi diperoleh:

ε = -n.D (b.KE.cos ωt) /dt

Seperti lapangan B Itu seragam dan area spase tidak bervariasi, mereka meninggalkan turunannya:

ε = -nba. D (cos ωt) /dt = ωnba. Sen ωt

Contoh 2

Loop memiliki luas 0.100 m² dan beralih ke 60.0 rev/s, dengan sumbu rotasi tegak lurus terhadap medan magnet seragam 0.200 t. Mengetahui bahwa kumparan memiliki 1000 belokan untuk menemukan: a) fem maksimum yang dihasilkan, b) orientasi koil dalam kaitannya dengan medan magnet ketika fem yang diinduksi maksimum terjadi.

Angka 8. Spiral N lap yang rusak di tengah medan magnet yang seragam dan menghasilkan sinyal sinus. Sumber: r. Serway, Fisika untuk Sains dan Teknik. Volume 2. Pembelajaran Cengage.

Larutan

a) fem maksimum adalah ε_Max = Ωnba

Sebelum melanjutkan untuk mengganti nilai, frekuensi 60 rev/s ke unit sistem internasional harus dilewati. Diketahui bahwa 1 revolusi setara dengan belokan atau 2p Radianes:

60.0 rev/s = 120p Radianes/s

ε_Max = 120p Radianes x 1000 lap x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Saat nilai ini terjadi Sen ωt = 1 Karena itu:

ωt = θ = 90º,

Dalam hal ini, bidang spiral paralel dengan B, sehingga vektor normal ke bidang tersebut membentuk 90º dengan lapangan. Ini terjadi ketika vektor hitam pada Gambar 8 tegak lurus terhadap vektor hijau yang mewakili medan magnet.

Referensi

1. Boylestad, r. 2011. Pengantar Analisis Sirkuit. 12. Edisi. Pearson. 327-376.
2. Figueroa, d. 2005. Elektromagnetisme. Seri Fisik untuk Sains dan Teknik. Volume 6. Diedit oleh d. Figueroa. Universitas Simon Bolivar. 115 dan 244-245.
3. Figueroa, d. 2006. Laboratorium Fisika 2. Equinox editorial. 03-1 dan 14-1.
4. Gelombang sinus. Pulih dari: iessierradegara.com
5. Serway, r. 2008.Fisika untuk Sains dan Teknik. Volume 2. Pembelajaran Cengage. 881-884