Fisik

Gelombang Unidimensional Ekspresi Matematika dan Contoh

Gelombang Unidimensional Ekspresi Matematika dan Contoh

Itu Gelombang unidimensional Mereka adalah orang -orang yang merambat dalam satu arah terlepas dari apakah getaran terjadi atau tidak dalam arah propagasi yang sama. Contoh yang baik dari mereka adalah gelombang yang bergerak di sepanjang tali tegang seperti gitar.

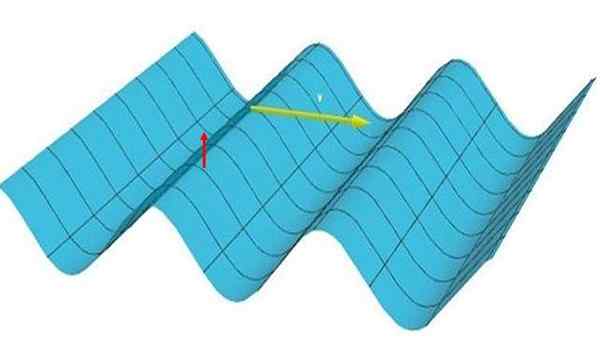
Dalam gelombang datar menyeberang, Partikel -partikel bergetar secara vertikal (mereka naik dan turun, melihat panah merah pada Gambar 1), tetapi itu adalah satu -dimensi karena gangguan tersebut bergerak dalam satu arah, mengikuti panah kuning.

Gambar 1: Gambar tersebut mewakili gelombang satu -dimensi. Perhatikan bahwa punggungan dan lembah membentuk garis paralel satu sama lain dan tegak lurus terhadap arah propagasi. Sumber: Made sendiri.

Gelombang unidimensional muncul cukup sering dalam kehidupan sehari -hari. Bagian berikut menjelaskan beberapa contohnya dan juga gelombang yang tidak tidak ada, untuk secara jelas menetapkan perbedaan.

[TOC]

Contoh gelombang unidimensional dan gelombang non -unidimensional

Gelombang unidimensional

Ini adalah beberapa contoh gelombang satu dimensi yang dapat dengan mudah diamati:

- Pulsa suara yang bergerak melalui bar lurus, karena itu adalah gangguan yang menyebar ke seluruh bar.

- Gelombang yang bergerak melalui saluran air, bahkan saat perpindahan permukaan air tidak sejajar dengan saluran.

- Gelombang yang menyebar di permukaan atau melalui ruang tiga dimensi juga bisa menjadi satu -dimensi, asalkan bagian depan gelombangnya sejajar satu sama lain dan bepergian dalam satu arah.

Gelombang non -dimensi

Contoh gelombang non -dimensi ditemukan dalam gelombang yang terbentuk pada permukaan air yang diam saat batu dijatuhkan. Ini adalah gelombang dua dimensi dari gelombang silinder.

Dapat melayani Anda: lengan tuasGambar 2. Gambar tersebut merupakan contoh dari apa yang bukan gelombang satu -dimensi. Perhatikan bahwa punggungan dan lembah membentuk lingkaran dan arah perambatan adalah radial ke luar, kemudian gelombang melingkar dua dimensi. Sumber: Pixabay.

Contoh lain dari gelombang dimensi non-serikat adalah gelombang suara yang menghasilkan petasan dengan ledakan pada ketinggian tertentu. Ini adalah gelombang tiga dimensi dengan bagian depan gelombang bola.

Ekspresi matematika dari gelombang satu -dimensi

Cara paling umum untuk mengekspresikan gelombang satu -dimensi yang menyebar tanpa atenuasi ke arah positif sumbu X dan dengan kecepatan v Itu secara matematis:

dan (x, t) = f (x - v.T)

Dalam ungkapan ini Dan mewakili gangguan pada posisi X Segera T. Bentuk gelombang diberikan oleh fungsi F. Misalnya, fungsi gelombang yang ditunjukkan pada Gambar 1 adalah:  dan (x, t) = cos (x - v t) dan gambar gelombang sesuai dengan momen t = 0.

Gelombang seperti ini, dijelaskan oleh fungsi kosinus atau sinus, disebut gelombang harmonik. Meskipun bukan satu -satunya bentuk gelombang yang ada, itu adalah yang paling penting, karena gelombang lain dapat direpresentasikan sebagai tumpang tindih atau jumlah gelombang harmonik. Itu adalah kenalan Teorema Fourier, jadi digunakan untuk menggambarkan sinyal dari semua jenis.

Saat gelombang bergerak ke arah negatif sumbu x, itu hanya berubah v oleh -v Dalam argumen, menjadi:

dan (x, t) = g (x + v t)

Gambar 3 menunjukkan animasi gelombang yang bergerak ke kiri: itu adalah bentuk yang disebut fungsi Lorentziana dan dia Ekspresi matematika adalah:

Dapat melayani Anda: bekerja: formula, unit, contoh, latihan

dan (x, t) = 1 / (1 + (x + 1⋅T)2

Dalam contoh ini, kecepatan propagasi adalah V = 1, -satuan ruang untuk setiap unit waktu-.

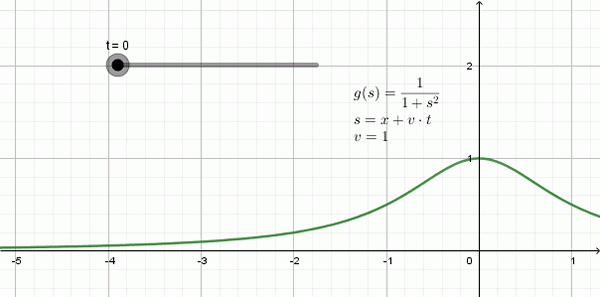Gambar 3. Contoh gelombang Lorentzian yang bergerak ke kiri dengan cepat v = 1. Sumber: disiapkan oleh f. Zapata dengan Geogebra.

Persamaan Gelombang Unidimensional

Persamaan gelombang adalah persamaan dalam turunan parsial, yang solusinya tentu saja merupakan gelombang. Itu membangun hubungan matematika antara bagian spasial dan bagian temporalnya, dan memiliki bentuk:

Solusi, yang justru fungsi y (x, t), dapat diverifikasi dengan penggantian dan pengembangan dalam persamaan ini. Misalnya, fungsi f (x - v t)  Dan  G (x + vt)  disebutkan, mereka adalah solusi persamaan gelombang.

Contoh terpecahkan

Kemudian Anda memiliki ekspresi umum y (x, t) untuk gelombang harmonik:

dan (x, t) = a⋅cos (k⋅x ± Ω⋅t + θo)

a) Jelaskan makna fisik parameter A, k, Ω Dan θo.

b) Arti apa yang dimiliki tanda -tanda ± pada argumen coseno?

c) Verifikasi bahwa ekspresi yang diberikan memang solusi dari persamaan gelombang dari bagian sebelumnya dan temukan kecepatannya v propagasi.

Solusi untuk)

Fitur gelombang ada di parameter berikut:

-KE mewakili amplitudo atau "tinggi gelombang".

-k masuk Nomor Gelombang Dan itu terkait dengan panjang gelombang λ melalui K = 2π/ λ.

-Ω Itu fekspansi sudut Dan itu terkait dengan periode T osilasi gelombang oleh

Ω = 2π/ t.

-θo Ini adalah tahap awal, yang terkait dengan titik awal gelombang.

Dapat melayani Anda: gesekan statis: koefisien, contoh, olahraga

Solusi b)

Tanda negatif diambil jika gelombang bergerak ke arah positif sumbu x dan tanda positif sebaliknya.

Solusi C)

Verifikasi bahwa ekspresi yang diberikan adalah solusi untuk persamaan gelombang sederhana: turunan parsial dari fungsi diambil dan (x, t) Mengenai x dua kali, sebagian berasal dari T dua kali dan kemudian kedua hasilnya memenuhi untuk mendapatkan kesetaraan:

Kedua berasal dari x: ∂2dan/ ∂x2= -K2. KE⋅cos (k⋅x ± Ω⋅t + θo)

Kedua berasal dari T: ∂2dan/ ∂t2= -Ω2. KE⋅cos (k⋅x ± Ω⋅t + θo)

Hasil ini diganti dalam persamaan gelombang:

 -k2. KE⋅cos (k⋅x ± Ω⋅t + θo) = (1/v2) (-Ω2. KE⋅cos (k⋅x ± Ω⋅t + θo))

Banyak KE Ketika kosinus disederhanakan, karena muncul di kedua sisi kesetaraan dan argumen kosinus adalah sama, oleh karena itu ekspresi dikurangi menjadi:

-k2 = (1/v2) (-Ω2)

Yang memungkinkan untuk mendapatkan persamaan v dengan kondisi Ω Dan k:

v2 = Ω2 / k2

v = ± Ω / k

Referensi

  1. E-pendidikan. Persamaan Gelombang Harmonik Unidimensional. Dipulihkan dari: E-Ducative.Cathedu.adalah
  2. The Rincón of Physics. Kelas gelombang. Diperoleh dari: Fisika.Blogspot.com.
  3. Figueroa, d. 2006. Gelombang dan fisika kuantum. Seri: Fisika untuk Sains dan Teknik. Diedit oleh Douglas Figueroa. Universitas Simon Bolivar. Caracas Venezuela.
  4. Lab Fisika. Gerakan Gelombang. Pulih dari: fisicalab.com.
  5. Peirce, a. Kuliah 21: Persamaan Gelombang Satu Dimensi: Solusi D'Alembert. Diperoleh dari: UBC.Ac.
  6. Persamaan Gelombang. Diperoleh dari: di.Wikipedia.com