Rumus ortoedro, area, volume, diagonal, contoh

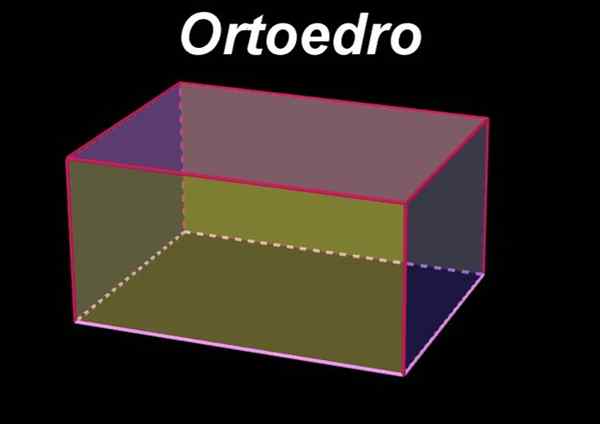
Dia Orthoedro Ini adalah figur geometris volumetrik atau tiga dimensi yang ditandai dengan memiliki enam wajah persegi panjang, sehingga wajah yang berlawanan berada di bidang paralel dan persegi panjang yang identik atau kongruen satu sama lain. Di sisi lain, wajah yang berdekatan dengan wajah yang diberikan berada di bidang yang tegak lurus dengan wajah awal.

Itu juga dapat dipertimbangkan saat Orthoedro sebagai prisma dasar persegi panjang ortogonal, di mana Sudut Dihedros Dibentuk oleh dua rencana yang berdekatan dengan tepi yang sama, mereka mengukur 90º. Sudut dihedral antara dua wajah diukur di persimpangan wajah dengan bidang tegak lurus dan umum untuk mereka.

Gambar 1. Orthoedro. Sumber: f. Zapata dengan Geogebra.

Demikian juga, ortoedro adalah a persegi panjang paralelepiped, Karena ini didefinisikan untuk paralelepiped sebagai sosok volumetrik dari enam wajah, yang paralel dua hingga dua.

Dalam paralelelepip, wajah -wajah adalah jajaran genjang, tetapi dalam persegi panjang paralelelepiped, wajah harus persegi panjang.

[TOC]

Bagian dari ortoedro

Bagian -bagian dari polyhedron, seperti orthoedro, adalah:

-Tepi

-Sudut 

-Wajah

Sudut antara dua tepi wajah orthoedro bertepatan dengan sudut dihedral yang dibentuk oleh dua wajah lainnya yang berdekatan dengan masing -masing tepi, membentuk sudut kanan. Gambar berikut mengklarifikasi setiap konsep:

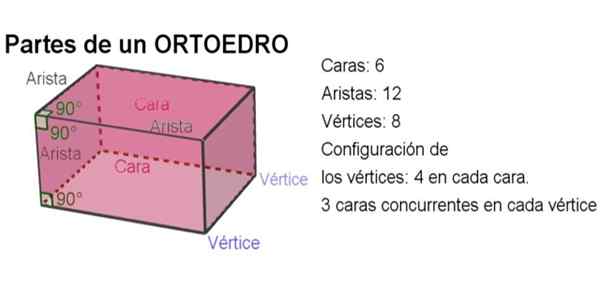Gambar 2. Bagian dari ortoedro. Sumber: f. Zapata dengan Geogebra.

-Total orthoedro memiliki 6 wajah, 12 tepi dan 8 simpul.

-Sudut antara dua tepi adalah sudut kanan.

-Sudut dihedral antara kedua sisi juga lurus.

-Di setiap wajah ada empat simpul dan di setiap simpul tiga wajah ortogonal yang saling hadir.

Dapat melayani Anda: apa itu nomor capicúa? Properti dan contoh

Rumus Orthoedro

Daerah

Permukaan atau area a Orthoedro Itu adalah jumlah area wajah mereka.

Jika tiga tepi yang disetujui dalam simpul memiliki ukuran A, B dan C, seperti yang ditunjukkan pada Gambar 3, maka wajah depan memiliki area C⋅b Dan wajah latar belakang juga memiliki area C⋅b.

Kemudian, dua wajah lateral memiliki area A⋅b setiap. Dan akhirnya, wajah lantai dan atap memiliki area A⋅c setiap.

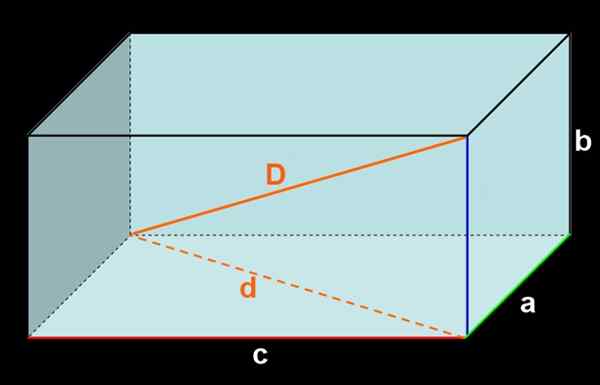Gambar 3. Orthoedro dimensi a, b, c. Diagonal D dan diagonal eksternal D.

Menambahkan area semua wajah diperoleh:

A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a

Menggambar faktor umum dan memesan istilah:

A = 2⋅ (a⋅b + b⋅c + c⋅a)

Volume

Jika orthoedro dianggap sebagai prisma, maka volumenya dihitung sebagai berikut:

Volume = Area dasar prisma x Ketinggian prisma

Dalam hal ini, lantai dimensi diambil sebagai persegi panjang C Dan ke, Jadi area dasarnya C⋅a.

Tinggi diberikan oleh panjangnya B Dari tepi ortogonal ke samping ke Dan C.

Mengalikan area dasar (A⋅c) dengan tinggi B Anda memiliki volume V Dari orthoedro:

V = A⋅b⋅c

Diagonal internal

Di orthoedro ada dua jenis diagonal: diagonal eksternal dan diagonal internal.

Diagonal eksternal berada pada wajah persegi panjang, sedangkan diagonal internal adalah segmen yang bergabung dengan dua simpul yang berlawanan, dipahami oleh simpul yang berlawanan yang tidak berbagi tepi.

Di orthoedro ada empat diagonal internal, semua ukuran yang sama. Panjang diagonal internal dapat diperoleh dari menerapkan teorema Pythagoras untuk persegi panjang.

Ini dapat melayani Anda: Fungsi Trigonometri: Dasar, di bidang Cartesian, Contoh, Latihan

Panjang D dari diagonal eksternal lantai orthoedro memenuhi hubungan Pythagoras:

D² = a² + C²

Demikian pula, diagonal pengukuran interior dari hubungan Pythagoras:

D² = d² + B².

Menggabungkan dua ekspresi sebelumnya yang Anda miliki:

D² = a² + C² + B².

Akhirnya, panjang salah satu diagonal internal orthoedro diberikan oleh formula berikut:

D = √ (a² + B² + C² ). 

Contoh

- Contoh 1

Seorang tukang batu membangun tangki berbentuk ortoedro yang dimensi internalnya adalah: basis 6 m x 4 m dan tinggi 2 m. Itu diminta:

a) Tentukan permukaan bagian dalam tangki jika benar -benar terbuka di bagian atasnya. 

b) Hitung volume ruang interior tangki.

c) Temukan panjang diagonal interior.

d) Berapa kapasitas tangki dalam liter?

Solusi untuk

Kami akan mengambil dimensi basis persegi panjang A = 4 m dan c = 6 m dan tinggi sebagai b = 2 m

Area ortoedro dengan dimensi yang diberikan diberikan oleh hubungan berikut:

A = 2⋅ (A⋅b + B⋅c + C⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

Artinya:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

Hasil sebelumnya adalah luas ortoedro yang ditutup dengan dimensi yang diberikan, tetapi karena itu adalah tangki yang benar -benar ditemukan di bagian atasnya, untuk mendapatkan permukaan dinding interior tangki, luas tutup yang hilang itu adalah:

C⋅a = 6 m ⋅ 4 m = 24 m².

Akhirnya, permukaan interior tangki adalah: S = 88 m² - 24 m² = 64 m².

Solusi b

Volume interior tangki diberikan oleh volume orthoedro dari dimensi interior tangki:

V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Solusi c

Diagonal interior Octahedron dengan dimensi interior tangki memiliki panjang yang diberikan oleh:

Dapat melayani Anda: variabel acak kontinu

√ (a² + B² + C² ) = √ ((4 m)² + (2 m)² + (6 m)² )

Melakukan operasi yang ditunjukkan yang kami miliki:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) m = 7.48 m.

Solusi d

Untuk menghitung kapasitas tangki dalam liter, perlu mengetahui bahwa volume desimeter kubik setara dengan kapasitas satu liter. Sebelumnya telah dihitung dalam volume dalam meter kubik, tetapi harus diubah menjadi desimeter kubik dan kemudian ke liter:

V = 48 m³ = 48 (10 dm)³ = 4.800 dm³ = 4.800 l

- Latihan 2

Aquarium kaca memiliki bentuk kubik sisi 25 cm. Tentukan area di M², Volume dalam liter dan panjang diagonal interior dalam cm.

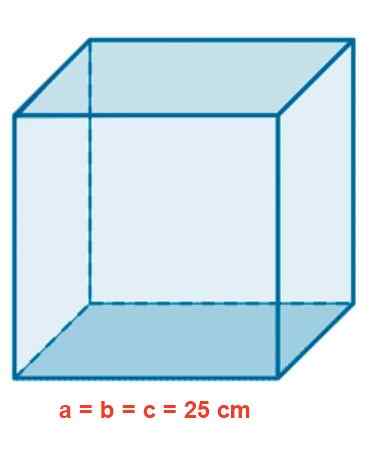Gambar 4. Akuarium kaca kubik.

Larutan

Area ini dihitung dengan formula ortoedro yang sama, tetapi dengan mempertimbangkan bahwa semua dimensi identik:

A = 2⋅ (3 a⋅a) = 6⋅ a² = 6⋅ (25 cm)² = 1.250 cm²

Volume kubus diberikan oleh:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15.625 dm³ = 15.625 l.

Panjang D dari diagonal interior adalah:

D = √ (3²) = 25√ (3) cm = 43,30 cm.

Referensi

1. Arias J. Geogebra: Prisma. Dipulihkan dari: YouTube.com.
2. Perhitungan.Dc. Latihan dan masalah terpecahkan di bidang dan volume. Pulih dari: perhitungan.Dc.
3. Salvador r. Piramida + Orthoedro dengan Geogebra (IHM). Dipulihkan dari: YouTube.com
4. Weisstein, Eric. "Ortoedro". Mathworld. Penelitian Wolfram.
5. Wikipedia. Orthoedro. Pulih dari: is.Wikipedia.com