Pasangan yang dipesan

Apa itu pasangan yang tertib?

Pasangan tertib atau duo Itu adalah satu set dua elemen yang ditulis sesuai dengan perintah yang ditetapkan oleh kriteria tertentu. Kriteria tersebut menentukan mana dari dua elemen yang lebih dulu dan mana yang mengejar.

Pasangan yang dipesan dilambangkan sebagai (x, y), di mana "x" adalah elemen pertama dari pasangan dan "y" adalah yang kedua, juga disebut Komponen. Secara umum (x, y) itu bukan torsi rapi yang sama (y, x). Dan selain urutan, karakteristik penting lain dari pasangan yang dipesan adalah kesetaraan: dua pasangan yang dipesan (a, b) dan (c, d) adalah sama hanya jika a = c dan b = d.

Gambar 1.- Berkat pasangan yang rapi, anak anjing itu tahu bahwa tulang-tulang itu terkubur di lokasi (3,1) dan (-4,2), sementara rumahnya ada di (0,0). Sumber: f. Zapata.

Contoh pasangan yang dipesan adalah mereka yang terdiri dari usia dan berat kursus siswa matematika. Pasangan yang dipesan (15, 62) sesuai dengan siswa berusia 15 tahun, berbeda dari pasangan yang tidak mungkin (62,15).

Konsep torsi yang dipesan sangat penting di berbagai bidang matematika, seperti pesawat Cartesian, pecahan, vektor di bidang, hubungan dan fungsi. Aspek penting adalah bahwa elemen mereka tidak selalu memiliki numerik, misalnya, mereka dapat dipesan dengan:

• Kota negara
• Nama Nama Belakang
• Suami istri

Dan banyak kombinasi lainnya.

Contoh pasangan yang dipesan

Pecahan

Sebuah fraksi direpresentasikan sebagai hasil bagi dua bilangan bulat P/Q, misalnya fraksi ½, yang setara dengan angka desimal 0.5.

Namun, fraksi ini bukan satu -satunya yang mewakili desimal 0.5, jadi lakukan hal berikut:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2)…

Dengan cara ini, fraksi apa pun dapat direpresentasikan sebagai pasangan tertib (p, q), di mana p dan q utuh, dengan p menempati posisi pembilang dan q. Ada batasan penting dan bahwa Q (penyebut) harus berbeda dari 0, karena fraksi bentuk p/0 tidak ditentukan.

Dapat melayani Anda: Himpunan terbatas: properti, contoh, latihan terpecahkan

Dan kondisi penting lainnya adalah bahwa dua fraksi A/B dan C/D sama selama dipenuhi bahwa:

A ∙ D = B ∙ C

Fungsi dan grafiknya

Suatu fungsi dapat dinyatakan sebagai satu set pasangan yang rapi. Misalnya, dengan memberi grafik fungsi di bidang Cartesian, elemen pertama ditetapkan posisi variabel independen, sedangkan yang kedua ditetapkan variabel dependen. Ini adalah pasangan yang tertib.

Untuk fungsi y = f (x), torsi rapi dapat dinyatakan sebagai [x, f (x)]]. Misalnya, pertimbangkan set awal:

A = 1, 2, 3, 4

Di set ini ada komponen pertama dari pasangan tertib sesuai dengan fungsi y = x². Set komponen kedua adalah:

B = 1, 4, 9, 16

Dan pasangan yang dipesan terbentuk adalah:

(1,1); (2,4); (3, 9); (4; 16)

Pandangan.

Vektor di pesawat

Vektor dapat diwakili dalam bidang cartesian dengan pasangan yang dipesan, di mana elemen pertama mewakili komponen horizontal "x" dan yang kedua komponen vertikal "y". Untuk membedakan vektor -vektor dari titik -titik di pesawat, mereka dilambangkan dengan huruf tebal dan tanda kurung persegi digunakan sebagai pengganti tanda kurung, seperti ini:

v =

Misalnya, vektor v = Memiliki komponen horizontal yang sama dengan 4 dan komponen vertikal sama dengan 7. Grafiknya adalah:

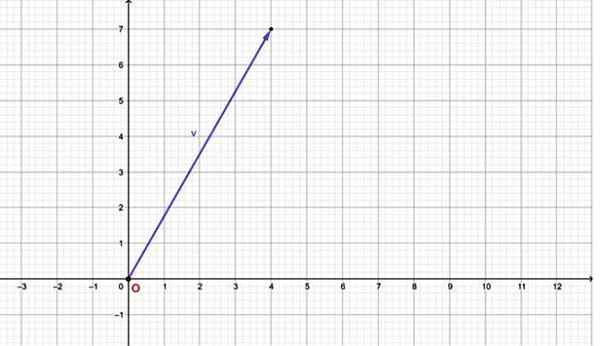Gambar 2.- Vektor pesawat dapat diekspresikan melalui pasangan yang tertib. Sumber: f. Zapata.

Perhatikan bahwa vektor ini memiliki asalnya bertepatan dengan asal sistem koordinat (0,0). Jika vektor memiliki asal pada titik lain, ia juga dapat diekspresikan dalam bentuk torsi tertib melalui pasangan yang tertib, untuk melakukannya melihat bagian berikut.

Dapat melayani Anda: hierarki operasi

Operasi Pares yang Dipesan

Tambahan

Biarkan target (a, b) dan (c, d) menjadi pasangan (d). Torsi baru diperoleh dengan jumlahnya menurut:

(a, b)+(c, d) = (a+c, b+d)

Elemen netral

Elemen netral dari penambahan pasangan yang dipesan adalah torsi (0,0), karena ketika ditambahkan ke pasangan yang dipesan (a, b), jumlahnya adalah yang terakhir:

(a, b) + (0,0) = (a, b)

Sebaliknya

Dengan menambahkan pasangan tertib (a, b) dengan kebalikannya (-a, -b) torsi tertib (0,0) diperoleh:

(a, b) + (-a, -b) = (0.0)

Komutativitas

Urutan penambahan tidak mengubah jumlah:

(a, b) + (c, d) = (c, d) + (a, b)

Asosiasi

Hasil penambahan tiga pasangan yang dipesan tidak diubah ketika dikelompokkan untuk melakukan operasi:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]]

Pengurangan pasangan yang dipesan

Biarkan target (a, b) dan (c, d) menjadi, pengurangan dilakukan sebagai berikut:

(a, b)-(c, d) = (a-c, b-d)

Produk

Dalam produk ada dua opsi: i) Lipat gandakan torsi yang dipesan dengan konstan dan ii) gandakan dua (atau lebih) rapi.

Penggandaan dengan konstan

Biarkan K menjadi konstan dan torsi tertib (A, B), produk antara konstanta dan torsi adalah:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Penggandaan pasangan yang dipesan

Produk antara pasangan yang dipesan (a, b) dan (c, d) dilakukan sebagai berikut:

(a, b) x (c, d) = (ac - bd, bc+iklan)

Elemen netral

Elemen netral dari perkalian adalah (1.0), karena dengan mengalikan torsi apa pun yang dipesan oleh ini, mengikuti aturan multiplikasi yang dijelaskan di atas, torsi asli adalah:

(a, b) x (1.0) = (a - 0, b + 0) = (a, b)

Dapat melayani Anda: invers multiplikasi: penjelasan, contoh, latihan terpecahkan

Asosiasi

Karena urutan faktor tidak mengubah produk, itu dapat dikelompokkan dengan cara yang berbeda untuk melipatgandakan tiga atau lebih pasangan rapi dan hasilnya sama:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]]

Latihan terpecahkan

Latihan 1

Anda telah memesan pasangan (x², X-2) = (16, 2). Yang merupakan nilai x?

Larutan

Menerapkan kesetaraan pasangan yang dipesan diperoleh terlebih dahulu:

X² = 16 ⇒ x₁ = 4, x₂ = -4

Untuk mengetahui mana dari dua nilai yang dipilih, penggunaan:

X-2 = 2

x = 2 + 2 = 4

Oleh karena itu, nilai x yang diminta adalah 4.

Latihan 2

Ekspresikan sebagai pasangan tertib vektor yang bergerak dari titik (1, 3) ke titik (7, 11) dan mewakili secara grafis.

Larutan

Menjadi v Vektor mencari. Untuk menentukan pasangan tertib yang mewakilinya, dan yang berisi koordinatnya, koordinat titik kedatangan dan titik asal dikurangi, dalam urutan itu. Jadi:

v = =

Vektor kemudian diwakili v seperti yang berubah dari (1.3) ke (7, 11) dan peralatan v yang asalnya ditetapkan untuk asal sistem koordinat (0,0). Seperti yang Anda lihat, mereka memiliki arah dan makna yang sama.

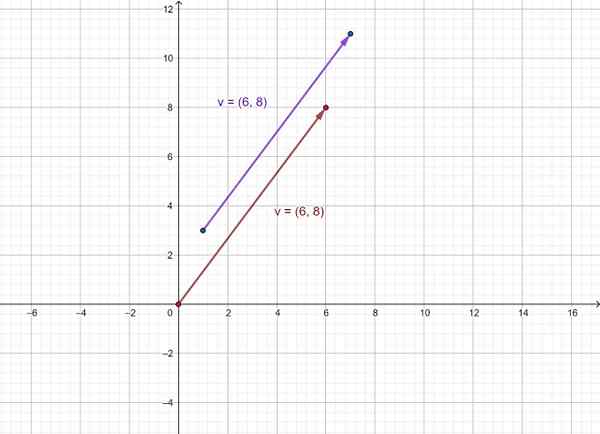Gambar 3. Representasi vektor sebagai pasangan yang tertib. Sumber: f. Zapata.

Referensi

1. Deepal. Pasangan yang dipesan. Dipulihkan dari: Deepai.org.
2. Mathemovil. Representasi Cartesius dari vektor oleh pasangan yang tertib. Pulih dari: matemovil.com.
3. Varsity Tutorrs. Pasangan yang dipesan. Diperoleh dari: WarsityTorm.com
4. Priestri, Juan. Hubungan dan fungsi. Fakultas Teknik. Departemen Matematika. Universitas Buenos Aires. Diperoleh dari: Subjek.fi.UBA.ar.
5. Universitas Denver. Hubungan. Pulih dari: matematika.Ucdenver.Edu.