Definisi paraboloid hiperbolik, sifat dan contoh

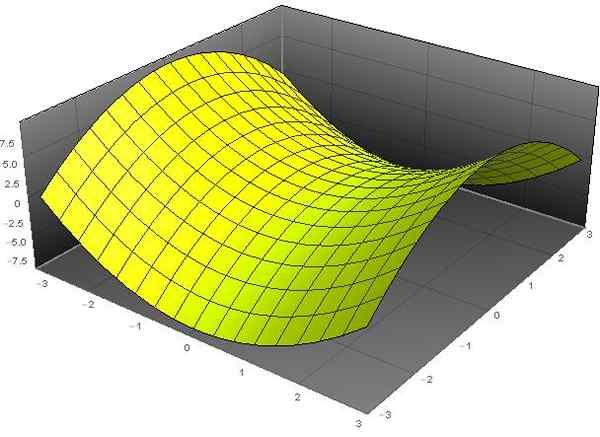
A Paraboloid hiperbolik Ini adalah permukaan yang persamaan umumnya dalam koordinat cartesian (x, y, z) memenuhi persamaan berikut:

(untuk)² - (dan B)² - Z = 0.

Denominasi "paraboloid" berasal dari fakta bahwa variabel z tergantung pada kotak variabel x dan y. Sementara kata sifat "hiperbolik" disebabkan oleh fakta bahwa persamaan hiperbola memiliki nilai z yang tetap dari z. Bentuk permukaan ini mirip dengan kursi berkuda kuda.

Gambar 1. Paraboloid hiperbolik z = x² - Dan². Sumber: f. Zapata melalui Wolfram Mathematica.

[TOC]

Deskripsi paraboloid hiperbolik

Untuk memahami sifat paraboloid hiperbolik, analisis berikut akan dibuat:

1.- Kasus tertentu akan diambil a = 1, b = 1, yaitu persamaan cartesian dari paraboloid tetap sebagai z = x² - Dan².

2.- Mereka dianggap paralel dengan pesawat ZX, yaitu y = ctte.

3.- Dengan y = ctte itu z = x² - C, yang mewakili perumpamaan dengan cabang atas dan simpul di bawah bidang xy.

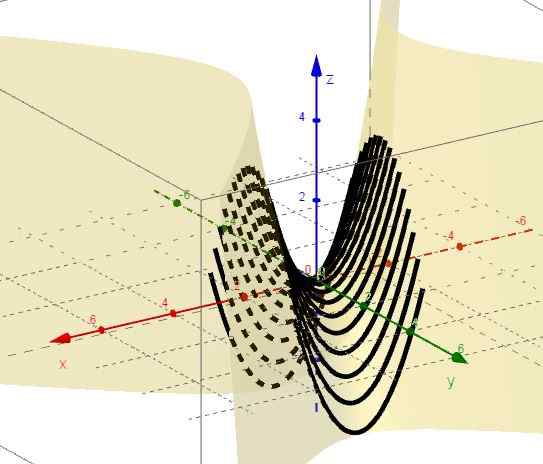Gambar 2. Keluarga kurva z = x² - C. Sumber: f. Zapata melalui Geogebra.

4.- Dengan x = ctte adalah z = c - y², yang mewakili perumpamaan dengan cabang ke bawah dan simpul di atas bidang xy.

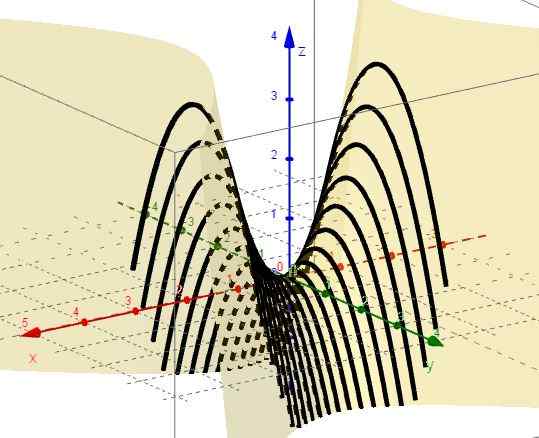Gambar 3. Keluarga kurva z = c - dan². Sumber: f. Zapata melalui Geogebra.

5.- Dengan z = ctte adalah c = x² - Dan², yang mewakili hiperbola di bidang yang sejajar dengan bidang XY. Ketika c = 0 Ada dua garis (A +45º dan -45º sehubungan dengan sumbu x) yang dicegat pada titik asal pada bidang XY.

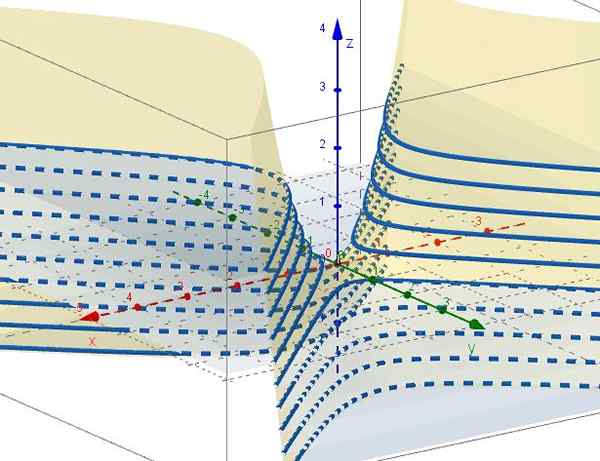Gambar 4. Keluarga kurva x² - Dan² = C. Sumber: f. Zapata melalui geogebra ..

Sifat paraboloid hiperbolik

1.- Empat titik berbeda dalam ruang tiga dimensi menentukan satu dan hanya paraboloid hiperbolik.

Itu dapat melayani Anda: membatasi sifat (dengan contoh)

2.- Paraboloid hiperbolik adalah a Permukaan yang diatur secara ganda. Ini berarti bahwa meskipun merupakan permukaan melengkung, untuk setiap titik paraboloid hiperbolik dua garis yang berbeda melewati sepenuhnya ke paraboloid hiperbolik. Permukaan lain yang bukan pesawat dan diatur ganda adalah Revolusi hiperboloid.

Justru sifat kedua dari paraboloid hiperbolik yang memungkinkan penggunaannya secara luas dalam arsitektur karena permukaan dapat dihasilkan dari balok atau string lurus.

Properti kedua dari paraboloid hiperbolik memungkinkan definisi alternatifnya: Ini adalah permukaan yang dapat dihasilkan oleh jalur seluler lurus yang sejajar dengan bidang tetap dan memotong dua garis tetap yang berfungsi sebagai panduan. Gambar berikut mengklarifikasi definisi alternatif paraboloid hiperbolik ini:

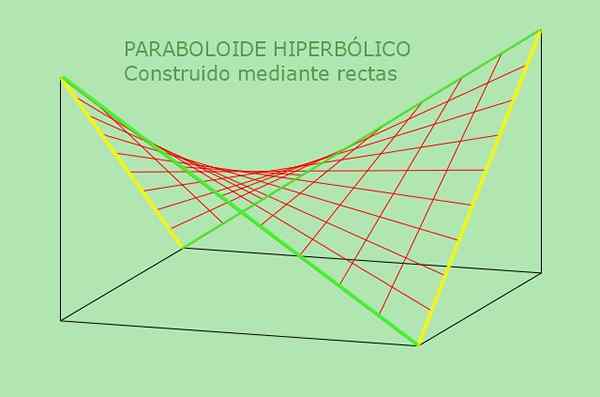Gambar 5. Paraboloid hiperbolik adalah permukaan yang diatur ganda. Sumber: f. Zapata.

Contoh terpecahkan

- Contoh 1

Menunjukkan bahwa persamaan: Z = xy, sesuai dengan paraboloid hiperbolik.

Larutan

Transformasi akan diterapkan dalam variabel x dan y yang sesuai dengan rotasi sumbu cartesian sehubungan dengan z dari sumbu +45. Koordinat X dan Y yang lama diubah menjadi X 'E dan' yang baru sesuai dengan hubungan berikut:

x = x ' - y'

y = x ' + dan'

Sementara koordinat z tetap sama, yaitu z = z '.

Dengan mengganti dalam persamaan z = x dan kami memiliki:

z '= (x' - y ') (x' + y ')

Saat menerapkan produk terkenal dari perbedaan dengan jumlah yang sama dengan perbedaan kotak itu adalah:

Z '= x'² - Dan'²

yang jelas sesuai dengan definisi yang awalnya diberikan paraboloid hiperbolik.

Intersepsi bidang yang sejajar dengan sumbu XY dengan paraboloid hiperbolik z = x dan menentukan hiperbola sama sisi yang memiliki asimptot bidang x = 0 e y = 0.

Dapat melayani Anda: Miletus teorema seperti itu

- Contoh 2

Tentukan parameternya ke Dan B dari paraboloid hiperbolik yang melewati titik -titik (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) dan D (2, -1, 32/9).

Larutan

Menurut sifatnya, empat titik dalam ruang tiga dimensi menentukan satu paraboloid hiperbolik tunggal. Persamaan umum adalah:

Z = (x/a)² - (dan B)²

Kami mengganti nilai yang diberikan:

Untuk poin A Anda memiliki 0 = (0/a)² - (0/b)², persamaan yang memenuhi nilai apa pun dari parameter a dan b.

Mengganti titik B diperoleh:

5/9 = 1/a² - 1 b²

Sedangkan untuk titik C tetap:

32/9 = 4/a² - 1 b²

Akhirnya, untuk titik D diperoleh:

32/9 = 4/a² - 1 b²

Yang identik dengan persamaan sebelumnya. Singkatnya, sistem persamaan harus diselesaikan:

5/9 = 1/a² - 1 b²

32/9 = 4/a² - 1 b²

Mengurangi persamaan kedua dari yang pertama diperoleh:

27/9 = 3/a² yang menyiratkan itu² = 1.

Demikian pula, persamaan kedua dari quadruple pertama dikurangi, memperoleh:

(32-20)/9 = 4/a² - 4/a² -1 b² + 4/b²

Yang disederhanakan sebagai:

12/9 = 3/b² ⇒ b² = 9/4.

Singkatnya, paraboloid hiperbolik yang melewati titik -titik A, B, C dan D yang diberikan memiliki persamaan Cartesian yang diberikan oleh:

Z = x² - (4/9) dan²

- Contoh 3

Menurut sifat paraboloid hiperbolik, dua baris yang sepenuhnya terkandung di dalamnya lulus untuk setiap titik. Untuk kasus z = x^2 - y^2 Temukan persamaan dari dua baris yang melewati titik p (0, 1, -1) jelas milik paraboloid hiperbolik, sehingga semua titik dari baris ini juga termasuk dalam sama.

Larutan

Menggunakan produk luar biasa dari perbedaan dalam kotak, persamaan paraboloid hiperbolik dapat ditulis sebagai berikut:

Dapat melayani Anda: segi empat: elemen, properti, klasifikasi, contoh

(x + y) (x - y) = c z (1/c)

Dimana c adalah konstanta non -zero.

Persamaan x + y = c z, dan persamaan x - y = 1/c sesuai dengan dua bidang dengan vektor normal N= y M=. Produk vektor m x n = Arah persimpangan garis dari dua bidang memberi kita. Kemudian salah satu garis yang melewati titik P dan milik paraboloid hiperbolik memiliki persamaan parametrik:

= + t

Untuk menentukan C kami mengganti titik p dalam persamaan x + y = c z, memperoleh:

C = -1

Demikian pula, tetapi mempertimbangkan persamaan (x - y = k z) dan (x + y = 1/k) Anda memiliki persamaan parametrik dari garis:

= + s dengan k = 1.

Singkatnya, kedua baris:

= + t y = + s

Mereka sepenuhnya terkandung dalam paraboloid hiperbolik z = x² - Dan² Melewati titik (0, 1, -1).

Sebagai cek, anggaplah t = 1 apa yang memberi kita intinya (1,2, -3) pada baris pertama. Anda harus memeriksa apakah itu juga pada paraboloid z = x² - Dan²:

-3 = 1² - 2² = 1 - 4 = -3

Yang menegaskan bahwa itu berlaku, itu milik permukaan paraboloid hiperbolik.

Paraboloid hiperbolik dalam arsitektur

Gambar 6. Oceanographic of Valencia (Spanyol).Sumber: Wikimedia Commons.

Paraboloid hiperbolik telah digunakan dalam arsitektur oleh arsitek avant-garde yang hebat, di antaranya nama-nama arsitek Spanyol Antoni Gaudí (1852-1926) dan sangat khususnya Spanyol juga Spanyol Félix Candela (1910-1997) sangat khusus.

Di bawah ini adalah beberapa karya berdasarkan paraboloid hiperbolik:

-Kapel Kota Cuernavaca (Meksiko) Pekerjaan oleh Arsitek Félix Candela.

-Oceanographic of Valencia (Spanyol), juga oleh Félix Candela.

Referensi

1. Encyclopedia of Mathematics. Permukaan yang diperintah. Pulih dari: ensiklopediaofmath.org
2. Llera Rubén. Paraboloid hiperbolik. Pulih dari: rubenllera.WordPress.com
3. Weisstein, Eric W. “Paraboloid hiperbolik.”Dari MathWorld-A Wolfram Web Resource. Dipulihkan dari: MathWorld.Wolfram.com
4. Wikipedia. Paraboloid. Diperoleh dari: di.Wikipedia.com
5. Wikipedia. Paraboloid. Pulih dari: is.Wikipedia.com
6. Wikipedia. Permukaan yang diperintah. Diperoleh dari: di.Wikipedia.com