Teorema mendasar dari demonstrasi aritmatika, aplikasi, latihan

Dia Teorema mendasar aritmatika Dia menyatakan bahwa angka alami apa pun yang lebih besar dari 1 dapat dipecah sebagai produk bilangan prima - memegang beberapa - dan formulir ini unik untuk angka itu, meskipun urutan faktornya bisa berbeda.

Ingatlah bahwa bilangan prima P Itu adalah salah satu yang hanya mengakui sebagai pembagi positif itu sendiri dan 1. Angka -angka berikut adalah sepupu: 2, 3, 5, 7, 11, 13 dan seterusnya, karena ada tak terbatas. Nomor 1 tidak dianggap sebagai sepupu, karena memiliki satu pembagi tunggal.

Gambar 1. Euclides (kiri) menunjukkan teorema mendasar aritmatika dalam elemen bukunya (350 a.C.), Dan demonstrasi lengkap pertama adalah karena Carl F. Gauss (1777-1855) (kanan). Sumber: Wikimedia Commons.

Untuk bagian mereka, angka yang tidak memenuhi di atas disebut nomor yang disusun, Sebagai 4, 6, 8, 9, 10, 12, 14 ... mari kita ambil nomor 10 misalnya dan segera kita melihat bahwa itu dapat dipecah sebagai produk 2 dan 5:

10 = 2 × 5

2 dan 5 memang, bilangan prima. Teorema menyatakan bahwa ini dimungkinkan untuk angka apa pun n:

Dimana hal₁, P₂, P₃… P_R Mereka adalah bilangan prima dan k₁, k₂, k₃,... k_R Mereka adalah bilangan alami. Jadi bilangan prima itu bertindak seperti batu bata yang darinya, dengan perkalian, bilangan alami dibangun.

[TOC]

Demonstrasi teorema mendasar aritmatika

Itu mulai menunjukkan bahwa setiap angka dapat terurai dalam faktor utama. Jadilah bilangan alami n> 1, sepupu atau senyawa.

Misalnya jika n = 2, dapat dinyatakan sebagai: 2 = 1 × 2, yang merupakan sepupu. Dengan cara yang sama kita melanjutkan dengan angka -angka berikut:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Kami terus seperti ini, membusuk semua bilangan alami sampai kami mencapai angka n -1. Mari kita lihat apakah kita bisa melakukannya dengan nomor berikut: n.

Jika n adalah sepupu, kita dapat menguraikannya sebagai n = 1 × n, tetapi anggaplah n disusun dan memiliki pembagi D, secara logis kurang dari n:

Dapat melayani Anda: statistik deskriptif: sejarah, karakteristik, contoh, konsep

1< d < n.

Ya n/d = p₁, dengan hal₁ Bilangan prima, maka n ditulis sebagai:

n = p₁.D

Jika D adalah sepupu tidak ada lagi yang bisa dilakukan, tetapi jika tidak, ada angka n₂ yang merupakan pembagi D dan kurang dari ini: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Untuk nomor sepupu lain p₂:

d = p₂ N₂

Bahwa dengan mengganti angka asli n akan memberikan:

n = p₁ .P₂ .N₂

Sekarang anggap n₂ Juga bukan bilangan prima dan kami menulisnya sebagai produk dari bilangan prima p₃, untuk pembagi miliknya₃, sedemikian rupa n₃ < n₂ < n₁ < n:

N₂ = p₃.N₃ → n = p₁ P₂ P₃.N₃

 Kami mengulangi prosedur ini beberapa kali terbatas sampai Anda mendapatkan:

n = p₁.P₂.P₃ … P_R

Ini berarti bahwa dimungkinkan untuk menguraikan semua bilangan bulat dari 2 ke angka n, sebagai produk bilangan prima.

Keunikan dekomposisi dalam faktor utama

Mari kita verifikasi sekarang kecuali untuk urutan faktor, dekomposisi ini unik. Misalkan Anda dapat menulis dengan dua cara:

n = p₁.P₂.P₃ … P_R = q_1.Q₂.Q₃… Q_S  (dengan r ≤ s)

Tentu saja q₁, Q₂, Q₃... mereka juga bilangan prima. Sebagai p₁ membagi menjadi (q_1.Q₂.Q₃… Q_S) Lalu hlm₁ Itu sama dengan salah satu dari "Q", tidak peduli Yang mana, jadi kita bisa mengatakan itu p₁ = q₁. Kami membagi n antara p₁ Dan kami mendapatkan:

P₂.P₃ … P_R =_.Q₂.Q₃… Q_S

Kami mengulangi prosedur untuk membagi segala sesuatu di antara p_R, Lalu kita mendapatkan:

1 = q_R+1… Q_S

Tetapi tidak mungkin untuk mencapai q_R+1… Q_S = 1 saat r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Aplikasi

Seperti yang telah kami katakan sebelumnya, bilangan prima mewakili jika Anda mau, atom angka, komponen dasar mereka. Jadi teorema mendasar aritmatika memiliki banyak aplikasi, yang paling jelas: kita dapat bekerja lebih mudah dengan jumlah besar jika kita mengekspresikannya sebagai produk dari angka yang lebih kecil.

Dapat melayani Anda: bilangan bulat

Dengan cara yang sama kita dapat menemukan beberapa umum maksimum (m.C.M.) dan pembagi umum maksimum (m.C.D.), Prosedur yang membantu kita membuat jumlah fraksi lebih mudah, menemukan akar dalam jumlah besar, atau beroperasi dengan radikal, merasionalisasi dan memecahkan masalah penerapan sifat yang sangat beragam.

Selain itu, bilangan prima sangat membingungkan. Pola belum dikenali di dalamnya dan tidak mungkin untuk mengetahui apa berikut ini. Yang terbesar sampai waktu ditemukan oleh komputer dan memiliki 24.862.048 digit, Meskipun bilangan prima baru lebih jarang muncul setiap saat.

Angka primo di alam

Cicadas, Cycaked atau Chicharras yang tinggal di timur laut Amerika Serikat muncul dalam 13 atau 17 tahun siklus. Keduanya adalah bilangan prima.

Dengan cara ini, chicharra menghindari bertepatan dengan predator atau pesaing yang memiliki periode kelahiran lainnya, atau berbagai varietas chicharra bersaing satu sama lain, karena mereka tidak bertepatan selama tahun yang sama.

Gambar 2. Cicada del este ajaib dari Amerika Serikat muncul setiap 13 atau 17 tahun. Sumber: PXFUEL.

Angka primo dan pembelian online

Nomor primo digunakan dalam kriptografi untuk menyimpan detail kartu kredit saat Anda membeli pembelian online. Dengan cara ini, data bahwa pembeli datang justru ke toko tanpa tersesat atau jatuh ke orang yang tidak bermoral.

Sebagai? Data kartu dikodekan dalam angka n yang dapat dinyatakan sebagai produk bilangan prima. Angka -bilangan prima ini adalah kunci yang mengungkapkan data, tetapi tidak diketahui oleh publik, mereka hanya dapat diterjemahkan di web yang diarahkan ke mana mereka diarahkan.

Mengurai angka menjadi faktor adalah tugas yang mudah jika angkanya kecil (melihat latihan diselesaikan), tetapi dalam hal ini mereka digunakan sebagai jumlah utama utama 100 digit, yang dengan mengalikannya memberikan jumlah yang jauh lebih besar, yang dekomposisi terperincinya menyiratkan a pekerjaan besar.

Dapat melayani Anda: perkiraan waktu

Latihan terpecahkan

- Latihan 1

Terurai 1029 menjadi faktor utama.

Larutan

1029 dapat dibagi dengan 3. Diketahui karena dengan menambahkan digit Anda jumlahnya adalah kelipatan 3: 1+0+2+9 = 12. Karena urutan faktor tidak mengubah produk, kita dapat mulai dari sana:

1029 3

343

1029 = 3 × 343

Di sisi lain 343 = 7³, Jadi:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

Dan karena 3 dan 7 adalah bilangan prima, ini adalah dekomposisi 1029.

- Latihan 2

Faktor trinomial x² + 42x + 432.

Larutan

Trinomial ditulis ulang dalam bentuk (x+a). (x+b) dan kita perlu menemukan nilai A dan B, sehingga:

A+b = 42; ke.B = 432

Angka 432 terurai menjadi faktor utama dan dari sana dipilih, oleh tanteo, kombinasi yang sesuai untuk fakta yang ditambahkan ke 42.

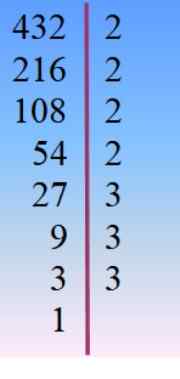
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

Dari sini ada beberapa kemungkinan untuk menulis 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

Dan semua dapat ditemukan dengan menggabungkan produk antara faktor -faktor utama, tetapi untuk menyelesaikan latihan yang diusulkan, satu -satunya kombinasi yang memadai adalah: 432 = 24 × 18 sejak 24 + 18 = 42, lalu:

X² + 42x + 432 = (x + 24). (x +18)

Referensi

1. Baldor, a. 1986. Aritmatika teoretis praktis. Editor Perusahaan Budaya Teks Amerika S.KE.
2. Dunia BBC. Kode Alam Tersembunyi. Diperoleh dari: BBC.com.
3. Dari Leon, Manuel.Nomor Primo: Penjaga Internet. Dipulihkan dari: blog.20 menit.adalah.
4. Unam. Teori Angka I: Teorema Fundamental Aritmatika. Diperoleh dari: Theoriadenumeros.Wikidot.com.
5. Wikipedia. Teorema mendasar aritmatika. Pulih dari: is.Wikipedia.org.