Paralelipiped

Paralelepiped adalah angka geometris enam sisi, di mana lawan saling paralel. Contoh: bata, kotak sepatu, ember, dll.

Apa itu paralelepiped?

A paralelipiped Ini adalah badan geometris yang dibentuk oleh enam wajah, yang karakteristik utamanya adalah bahwa semua wajahnya adalah jajaran genjang dan juga wajahnya yang berlawanan saling sejajar. Ini adalah polyhedron yang umum dalam kehidupan kita sehari -hari, karena kita dapat menemukannya dalam kotak sepatu, bentuk batu bata, bentuk microwave, dll.

Menjadi polyhedron, paralelepiped berisi volume terbatas dan semua wajahnya datar. Itu adalah bagian dari kelompok prisma, yang merupakan polyhedra di mana semua simpulnya terkandung dalam dua bidang paralel.

Elemen paralelepiped

Wajah

Mereka adalah masing -masing daerah yang dibentuk oleh jajaran genjang yang membatasi paralelelepiped. Paralelepiped memiliki enam wajah, di mana setiap wajah memiliki empat wajah yang berdekatan dan sebaliknya. Selain itu, setiap wajah sejajar dengan kebalikannya.

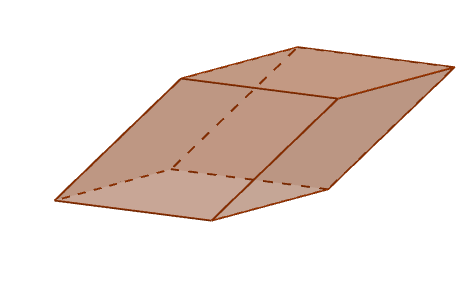Perspektif Paralelepiped

Tepi

Mereka adalah sisi umum dari dua wajah. Secara total, paralelepiped memiliki dua belas tepi.

Puncak

Ini adalah titik umum dari tiga wajah yang berdekatan dua hingga dua. Paralelepiped memiliki delapan simpul.

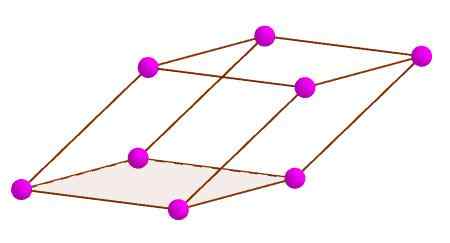Simpul dari paralelelepiped

Diagonal

Mengingat dua wajah dari paralelelepiped berlawanan satu sama lain, kita dapat menggambar segmen garis yang beralih dari titik satu wajah ke titik berlawanan dari yang lain.

Segmen ini dikenal sebagai diagonal paralelepiped. Setiap paralelepiped memiliki empat diagonal.

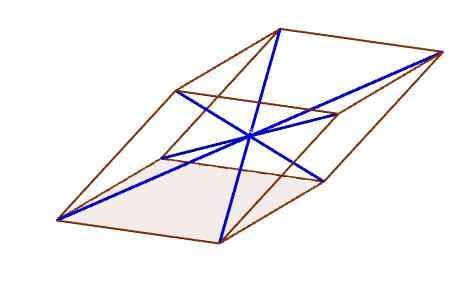Diagonal paralelepiped

Tengah

Itu adalah titik di mana semua diagonal berpotongan.

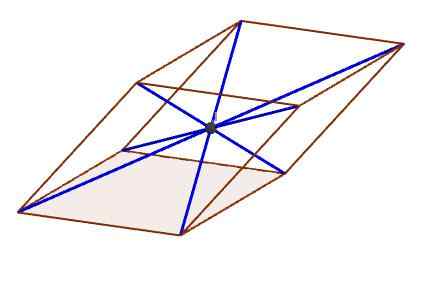Titik gambar menunjukkan pusat, di mana semua diagonal berpotongan

Karakteristik paralelepiped

Seperti yang telah kami sebutkan, badan geometris ini memiliki dua belas tepi, enam wajah dan delapan simpul.

Dalam paralelepiped, tiga set yang dibentuk oleh empat tepi dapat diidentifikasi, yang sejajar satu sama lain. Selain itu, tepi set ini juga mematuhi properti memiliki panjang yang sama.

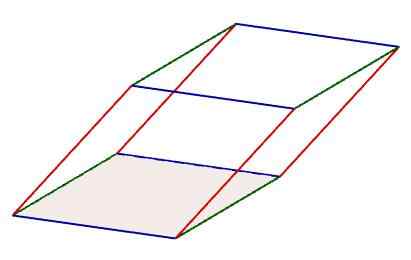Karakteristik paralelepiped

Properti lain berpose.

Selain itu, paralelepiped, menjadi cembung polyhedros, mematuhi teorema Euler untuk polyhedros, yang memberi kita hubungan antara jumlah wajah, jumlah tepi dan jumlah simpul. Hubungan ini diberikan dalam bentuk persamaan berikut:

C + V = A + 2

Fitur ini dikenal sebagai karakteristik Euler. Di mana c adalah jumlah wajah, dan jumlah simpul dan jumlah tepi.

Jenis paralleepípedos

Kita dapat mengklasifikasikan paralelepípe berdasarkan wajah mereka, pada jenis berikut:

Orthoedro

Mereka adalah paralelepípe di mana wajah mereka terdiri dari enam persegi panjang. Setiap persegi panjang tegak lurus dengan mereka yang berbagi tepi. Mereka adalah yang paling umum dalam kehidupan kita sehari -hari, ini adalah bentuk sepatu dan kotak bata yang biasa.

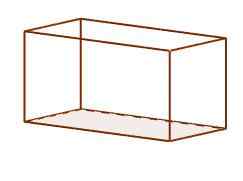Orthoedro paralelepiped

Kubus atau hexaedro biasa

Ini adalah kasus khusus dari yang sebelumnya, di mana masing -masing wajah adalah kuadrat.

Dapat melayani Anda: elipsKubus atau hexaedro biasa

Kubus juga merupakan bagian dari badan geometris yang disebut Platonic Solids. Solid platonik adalah polyhedron cembung, sehingga kedua wajahnya dan sudut internalnya sama dengan satu sama lain.

Romboedro

Itu adalah paralelepiped yang memiliki belah ketupat. Belah ketupat ini semuanya sama satu sama lain, karena mereka berbagi tepi.

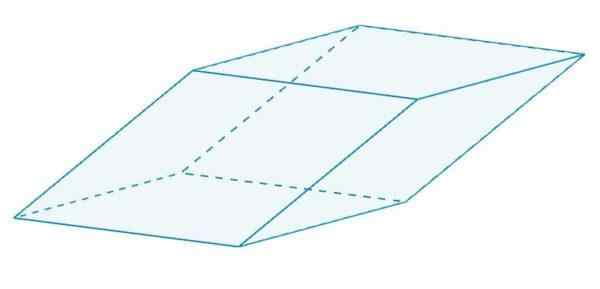Seorang romboedro

Romboiedro

Enam wajahnya adalah rhomboid. Ingatlah bahwa rhomboid adalah poligon empat sisi dan empat sudut yang sama dengan dua hingga dua. Rhomboids adalah jajaran genjang yang bukan persegi, atau persegi panjang, atau belah ketupat.

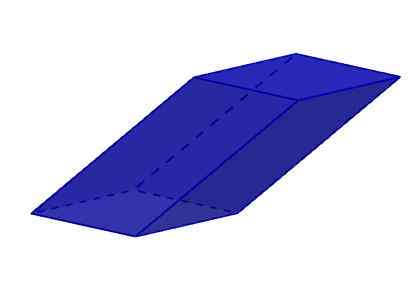Romboiedro

Di sisi lain, miring paralelepiped adalah yang di mana setidaknya satu ketinggian tidak cocok dengan tepinya. Dalam klasifikasi ini kita dapat memasukkan rhomboedros dan rhomboiedros.

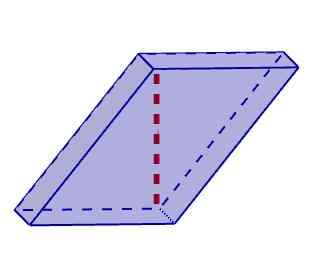Miring paralelepiped

Perhitungan diagonal

Untuk menghitung diagonal orthoedro kita dapat menggunakan teorema pythagoras untuk r³.

Ingatlah bahwa ortoedro memiliki karakteristik bahwa masing -masing pihak tegak lurus dengan sisi yang berbagi tepi. Dari fakta ini kita dapat menyimpulkan bahwa setiap tepi tegak lurus dengan yang berbagi verteks.

Untuk menghitung panjang diagonal orthoedro kami melanjutkan sebagai berikut:

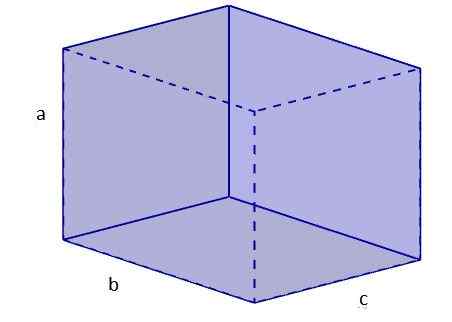
1. Kami menghitung diagonal salah satu wajah, yang akan kami taruh berdasarkan basis. Untuk ini kami menggunakan teorema Pythagoras. Mari beri nama diagonal d itu_B.

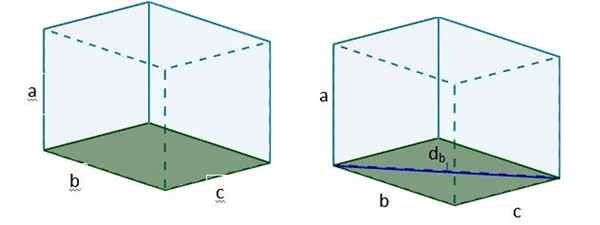
2. Lalu dengan d_B Kita dapat membentuk segitiga persegi panjang baru, sehingga hipotenuse dari segitiga ini adalah diagonal D yang dicari.

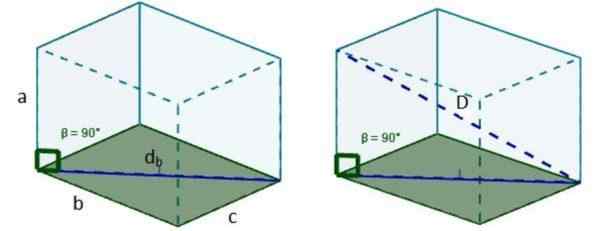
3. Kami menggunakan teorema Pythagoras lagi dan kami memiliki panjang diagonal itu adalah:

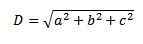
Cara lain untuk menghitung diagonal dengan cara yang lebih grafis adalah dengan jumlah vektor bebas.

Ingatlah bahwa dua vektor bebas A dan B ditambahkan dengan menempatkan ekor vektor B dengan ujung vektor a.

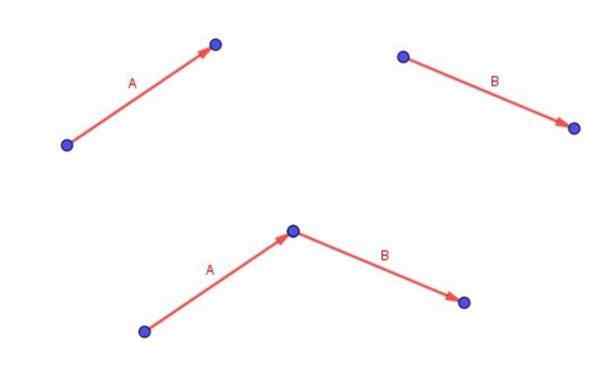
Vektor (a + b) adalah yang dimulai di ekor A dan diakhiri di ujung b.

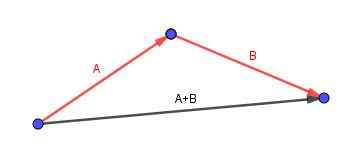
Pertimbangkan paralelelepiped yang ingin kami hitung diagonal. Kami mengidentifikasi tepi dengan vektor berorientasi yang nyaman.

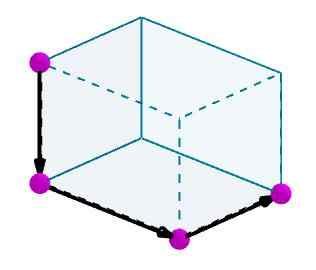
Kemudian kami menambahkan vektor -vektor ini dan vektor yang dihasilkan akan menjadi diagonal dari paralelepiped.

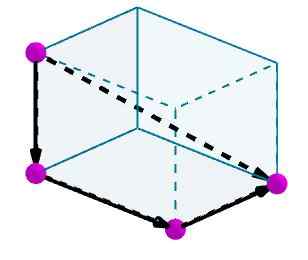
Area paralelelepiped

Area paralelepiped diberikan oleh jumlah masing -masing area wajahnya.

Jika kita menentukan salah satu sisi sebagai dasar,

KE_L + 2nd_B = Area Total

Kemana_L Itu sama dengan jumlah area dari semua sisi yang berdekatan dengan pangkalan, yang disebut area samping dan ke_B Itu adalah area dasar.

Bergantung pada jenis paralelepiped yang dengannya kami bekerja, kami dapat menulis ulang formula tersebut.

Area orthoedro

Diberikan oleh formula

A = 2 (AB + BC + CA).

Contoh 1

Mengingat ortoedro berikut, dengan sisi A = 6 cm, b = 8 cm dan c = 10 cm, hitung area paralelepiped dan panjang diagonalnya.

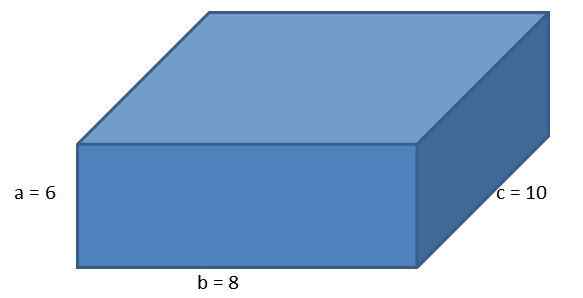
Menggunakan rumus untuk area orthoedro yang harus kita lakukan

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Perhatikan bahwa sebagai orthoedro adalah panjang salah satu dari empat diagonalnya adalah sama.

Itu dapat melayani Anda: integral tidak terbatas: properti, aplikasi, perhitungan (contoh)

Menggunakan Teorema Pythagoras untuk Ruang

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Area kubus

Karena setiap tepi memiliki panjang yang sama, kami memiliki a = b dan a = c. Mengganti dalam formula sebelumnya yang kami miliki

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6a²

Contoh 2

Kotak konsol game memiliki bentuk kubus. Jika kita ingin membungkus kotak ini dengan kertas hadiah, berapa banyak kertas yang akan kita habiskan untuk mengetahui bahwa panjang tepi kubus adalah 45 cm?

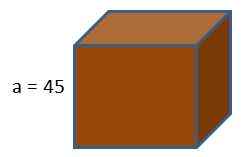
Menggunakan rumus area kubus kami mendapatkannya

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Area rhomboedro

Karena semua wajahnya sama, itu cukup untuk menghitung luas salah satunya dan melipatgandakannya dengan enam.

Kami memiliki bahwa area belah ketupat dapat dihitung dengan diagonalnya dengan formula berikut

KE_R = (Dd)/2

Menggunakan formula ini mengikuti bahwa total luas rhomboedro adalah

KE_T = 6 (dd)/2 = 3dd.

Contoh 3

Wajah rhomboedro berikutnya dibentuk oleh belah ketupat yang diagonalnya adalah d = 7 cm dan d = 4 cm. Daerah Anda akan

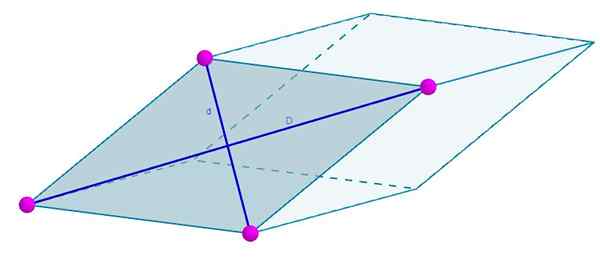
A = 3 (7 cm) (4 cm) = 84 cm².

Area rhomboiedro

Untuk menghitung luas rhomboiedro kita harus menghitung luas rhomboid yang menyusunnya. Karena paralelelepiped memenuhi properti bahwa sisi yang berlawanan memiliki area yang sama, kita dapat mengaitkan sisi dalam tiga rekan.

Dengan cara ini kami memiliki daerah Anda

KE_T = 2b₁H₁ + 2b₂H₂ + 2b₃H₃

Dimana b_yo adalah pangkalan yang terkait dengan sisi dan h_yo Tinggi relatifnya sesuai dengan pangkalan tersebut.

Contoh 4

Pertimbangkan paralelelepipasi berikut,

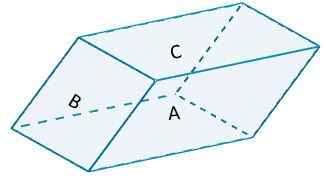
Di mana sisi A dan sisi A '(sisi berlawanan mereka) didasarkan B = 10 dan per tinggi h = 6. Area yang ditandai akan memiliki nilai

KE₁ = 2 (10) (6) = 120

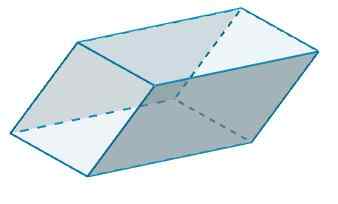
B dan b 'memiliki b = 4 dan h = 6, lalu

KE₂ = 2 (4) (6) = 48

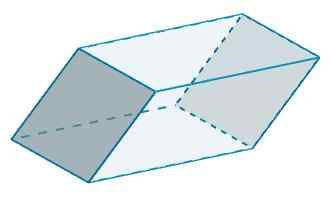
Dan c dan c 'memiliki b = 10 dan h = 5, juga

KE₃ = 2 (10) (5) = 100

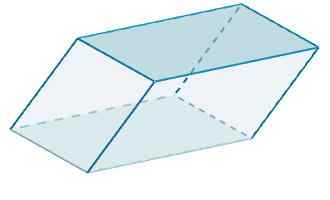
Akhirnya area rhomboiedro

A = 120 + 48 + 100 = 268.

Volume paralelepiped

Formula yang memberi kita volume paralelelepiped adalah produk dari luas salah satu wajahnya karena ketinggian yang sesuai dengan wajah tersebut.

V = a_CH_C

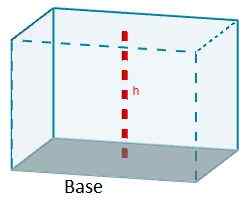
Tergantung pada jenis paralelepiped, formula ini dapat disederhanakan.

Dengan demikian kita memiliki, misalnya, bahwa volume orthoedro akan diberikan oleh

V = ABC.

Di mana a, b dan c mewakili panjang tepi ortoedro.

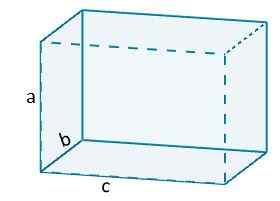
Dan dalam kasus tertentu dari kubus

V = a³

Contoh 1

Ada tiga model berbeda untuk kotak cookie dan Anda mau.

Yang pertama adalah kubus yang tepi memiliki panjang a = 10 cm.

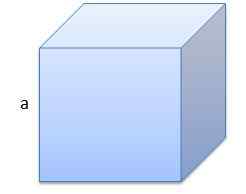
Volumenya akan menjadi V = 1000 cm³

Yang kedua adalah b = 17 cm, c = 5 cm, d = 9 cm.

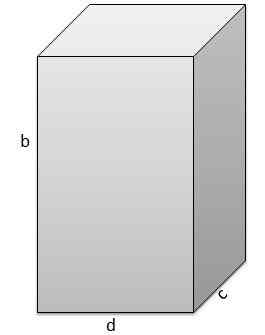
Dan karena itu volumenya adalah V = 765 cm³

Dan yang ketiga memiliki E = 9 cm, f = 9 cm dan g = 13 cm.

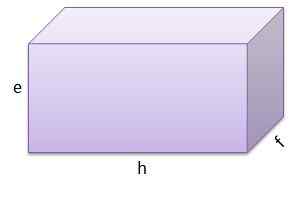
Dan volumenya adalah V = 1053 cm³

Dapat melayani Anda: jenis sudut, karakteristik, dan contoh

Oleh karena itu, kotak dengan volume terbesar adalah yang ketiga.

Metode lain untuk mendapatkan volume paralelepiped adalah menggunakan aljabar vektor. Secara khusus, produk skalar triple.

Salah satu interpretasi geometris dari produk skalar triple adalah volume paralelelepiped, yang ujung -ujungnya adalah tiga vektor yang memiliki simpul yang sama dengan titik awal.

Dengan cara ini, jika kita memiliki paralelelepiped dan kita ingin tahu apa volumenya, itu cukup untuk mewakilinya dalam sistem koordinat di R³ bertepatan dengan salah satu simpulnya dengan asalnya.

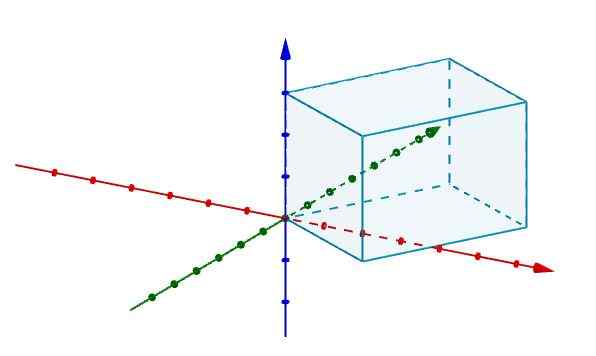
Lalu kami mewakili tepi yang setuju pada titik asal dengan vektor, seperti yang ditunjukkan pada gambar.

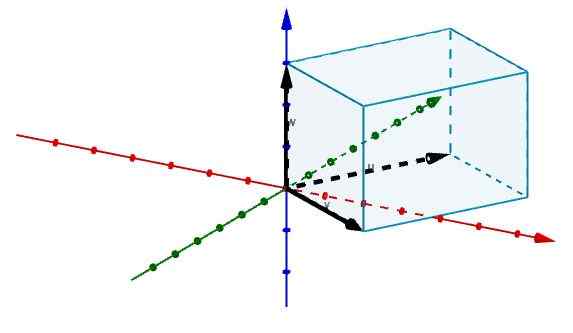
Dan dengan cara ini kita memiliki volume paralelelepiped tersebut diberikan oleh

V = | AXB ∙ C |

Atau setara, volume adalah penentu matriks 3 × 3, yang dibentuk oleh komponen vektor tepi.

Contoh 2

Dengan mewakili paralelelepipasi berikut di R³ Kita dapat melihat bahwa vektor yang menentukan sebagai berikut

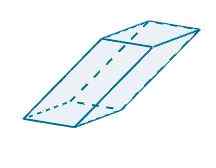
u = (-1, -3.0), v = (5, 0, 0) dan w = (-0.25, -4, 4)

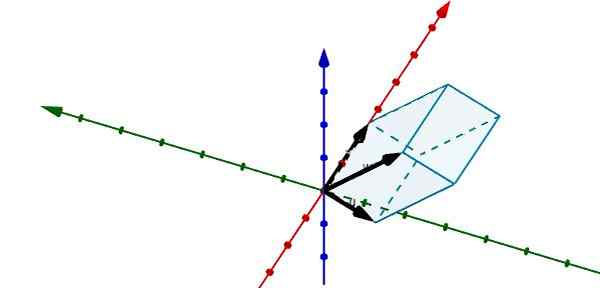
Menggunakan produk triple skalar yang kami miliki

V = | (UXV) ∙ W |

Uxv = (-1, -3.0) x (5, 0, 0) = (0.0, -15)

(Uxv) ∙ w = (0,0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

Ini menyimpulkan bahwa v = 60

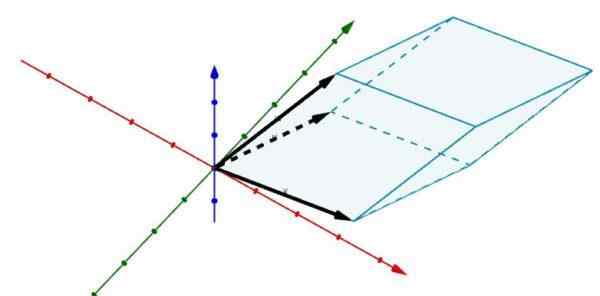
Pertimbangkan sekarang paralelelepipasi berikut di R³ yang ujungnya ditentukan oleh vektor

A = (2, 5, 0), b = (6, 1, 0) dan c = (3, 4, 4)

Menggunakan faktor penentu memberi kita itu

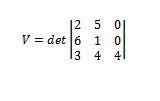
Dengan demikian kita memiliki volume paralelelepiped adalah 112.

Keduanya adalah cara yang setara untuk menghitung volume.

Paralelepiped yang sempurna

Ia dikenal sebagai bata euler (atau blok euler) ke orthoedro yang memenuhi properti yang panjang tepi dan panjang diagonal masing -masing wajahnya adalah bilangan bulatnya.

Sementara Euler bukan ilmuwan pertama yang mempelajari orthoeders yang memenuhi properti itu, dia memang menemukan hasil yang menarik tentang mereka.

Bata Euler terkecil ditemukan oleh Paul Halcke (1662-1731) dan panjang ujungnya adalah A = 44, b = 117 dan C = 240.

Masalah terbuka dalam teori angka adalah sebagai berikut:

Apakah ada orthoeder yang sempurna?

Saat ini, pertanyaan ini masih belum memiliki jawaban, karena belum mungkin untuk membuktikan bahwa tidak ada tubuh, tetapi belum ada yang ditemukan.

Apa yang telah ditunjukkan sejauh ini adalah bahwa paralelelepiped yang sempurna melakukannya. Yang pertama ditemukan memiliki panjang tepi nilai 103, 106 dan 271.

Referensi

1. Guy, r. (1981). Masalah yang belum terpecahkan dalam teori angka. Peloncat.
2. Landaverde, f. D. (1997). Geometri. Kemajuan.
3. Leithold, l. (1992). Perhitungan dengan geometri analitik. Harla, s.KE.
4. Rendon, a. (2004). Gambar Teknis: Notebook Aktivitas 3 Baccalaureate 2nd. Tebar.
5. Resnick, r., Halliday, d., & Krane, k. (2001). Fisika Vol. 1. Meksiko: benua.