Perimeter Lingkaran Cara Keluar dan Formula, Latihan Terpecahkan

Dia Perimeter lingkaran Itu adalah himpunan titik yang membentuk kontur lingkaran dan juga dikenal sebagai panjang keliling. Itu tergantung pada jari -jari, karena keliling yang lebih besar jelas akan memiliki kontur yang lebih besar.

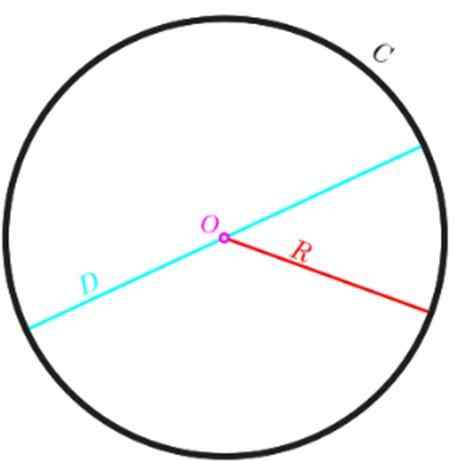
Menjadi P Perimeter lingkaran dan R jari -jari yang sama, maka kita bisa menghitung P Dengan persamaan berikut:

P = 2π.R

Perimeter lingkaran (dalam hal ini pizza) tergantung pada radionya. Sumber: Pixabay.

Di mana π adalah bilangan real (membaca "pi") yang bernilai sekitar 3.1416 ... poin -poin suspensi adalah karena fakta bahwa π memiliki desimal yang tak terbatas. Oleh karena itu, saat membuat perhitungan, perlu untuk membulatkan nilainya.

Namun, untuk sebagian besar aplikasi, cukup untuk mengambil jumlah yang ditunjukkan di sini, atau menggunakan semua desimal yang dengannya kalkulator yang bekerja.

Jika alih -alih memiliki jari -jari, lebih disukai menggunakan diameter D, yang kita tahu adalah dua kali jari -jari, perimeter dinyatakan sebagai berikut:

P = π.2r = π.D

Karena perimeter panjangnya, ia harus selalu diekspresikan dalam unit seperti meter, sentimeter, kaki, inci dan banyak lagi, tergantung pada sistem yang lebih disukai.

[TOC]

Lingkaran dan lingkaran

Mereka sering kali digunakan secara bergantian, yaitu, sebagai sinonim. Tetapi kebetulan ada perbedaan di antara mereka.

Kata "perimeter" berasal dari "periode" bahasa Yunani yang berarti kontur dan "kereta bawah tanah" atau mengukur. Lingkar adalah kontur atau perimeter lingkaran. Secara formal didefinisikan:

Lingkar adalah himpunan titik dengan jarak yang sama ke titik yang disebut pusat, jarak ini menjadi jari -jari lingkar.

Untuk bagiannya, lingkaran didefinisikan sebagai berikut:

Lingkaran adalah himpunan titik yang jaraknya ke titik yang disebut pusat kurang dari atau sama dengan jarak tetap yang disebut radio.

Pembaca dapat memperingatkan perbedaan halus antara kedua konsep. Lingkar hanya mengacu pada himpunan titik tepi, sedangkan lingkaran adalah himpunan titik dari tepi ke bagian dalam, di mana kelilingnya adalah perbatasan.

Dapat melayani Anda: latihan izin formula

Latihan DEmostrasi perhitungan perimeter lingkaran

Melalui latihan berikut, konsep yang dijelaskan akan dipraktikkan, serta beberapa lainnya yang akan dijelaskan saat mereka muncul. Kami akan mulai dari yang paling sederhana dan tingkat kesulitan akan meningkat secara progresif.

- Latihan 1

Temukan perimeter dan area lingkaran radio 5 cm.

Larutan

Persamaan yang diberikan pada awalnya diterapkan secara langsung:

P = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

Untuk menghitung area tersebut KE Formula berikut digunakan:

KE = π.R² = π. (5cm)²= 25π cm²= 78.534 cm²

- Latihan 2

a) Temukan perimeter dan luas daerah kosong dari gambar berikut. Pusat lingkaran teduh berada di titik merah, sedangkan pusat lingkar putih adalah titik hijau.

b) Ulangi bagian sebelumnya untuk wilayah yang teduh.

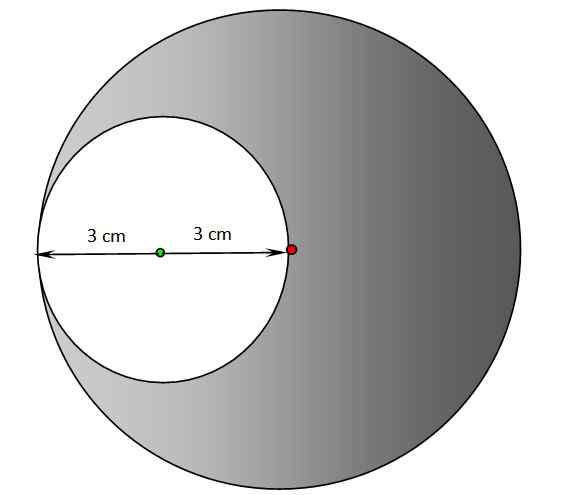Lingkaran untuk Latihan 2. Sumber: f. Zapata.

Larutan

a) Jari -jari lingkar putih adalah 3 cm, oleh karena itu kami menerapkan persamaan yang sama seperti dalam Latihan 1:

P = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

KE = π.R² = π. (3cm)²= 9π cm²= 28.27 cm²

b) Untuk lingkaran yang diarsir, jari -jari adalah 6 cm, perimeternya dua kali yang dihitung di bagian A):

P = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

Dan akhirnya luas wilayah yang teduh dihitung sebagai berikut:

- Pertama adalah area lingkaran teduh seolah -olah sudah lengkap, yang akan kita sebut ', seperti ini:

KE' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Kemudian ke daerah tersebut KE' Area lingkaran putih dikurangi, yang sebelumnya dihitung di bagian A), dengan cara ini area yang diminta diperoleh, yang akan dilambangkan hanya sebagai:

A = a ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Latihan 3

Temukan area dan perimeter wilayah yang diarsir pada gambar berikut:

Dapat melayani Anda: sudut tambahan: apa itu, perhitungan, contoh, latihan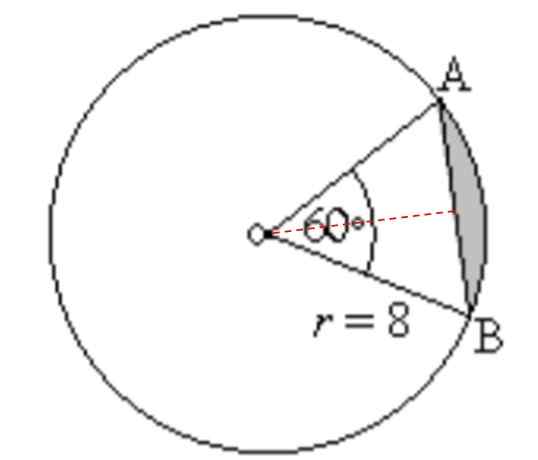Gambar untuk Latihan 3. Sumber: f. Zapata.

Larutan

Perhitungan luas wilayah yang teduh

Pertama -tama kami menghitung area Sektor melingkar atau wedge, antara segmen lurus OA dan OB dan segmen AB melingkar, seperti yang ditunjukkan pada gambar berikut:

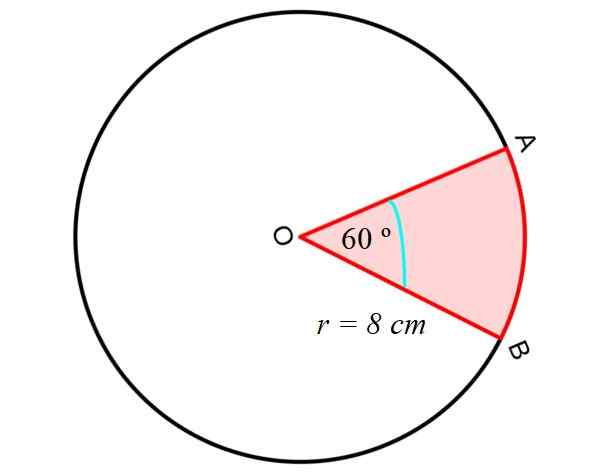
Untuk ini, persamaan berikut digunakan, yang memberi kita luas sektor melingkar, mengetahui jari -jari R dan sudut tengah antara segmen OA dan OB, yaitu, dua radio lingkar:

KE _{Sektor melingkar} = Π.R². (αº/360º)

Di mana αº adalah sudut pusat - itu adalah pusat karena simpulnya adalah pusat keliling - antara dua radio.

Langkah 1: Perhitungan area sektor melingkar

Dengan cara ini, area sektor yang ditunjukkan pada gambar adalah:

KE _{Sektor melingkar} = Π.R². (αº/360º) = π. (8 cm)². (60º/360º) = (64/6) π cm²= 33.51 cm²

Langkah 2: Perhitungan area segitiga

Kemudian kami akan menghitung area segitiga putih pada Gambar 3. Segitiga ini sama -sama dan luasnya:

KE _{segi tiga} = (1/2) Basis x Tinggi

Tinggi adalah garis merah putus -putus yang terlihat pada Gambar 4. Untuk menemukannya, Anda dapat menggunakan teorema Pythagoras, misalnya. Tapi itu bukan satu -satunya cara.

Pembaca pengamat akan memperhatikan bahwa segitiga sama sisi dibagi menjadi dua persegi panjang yang identik, yang alasnya 4 cm:

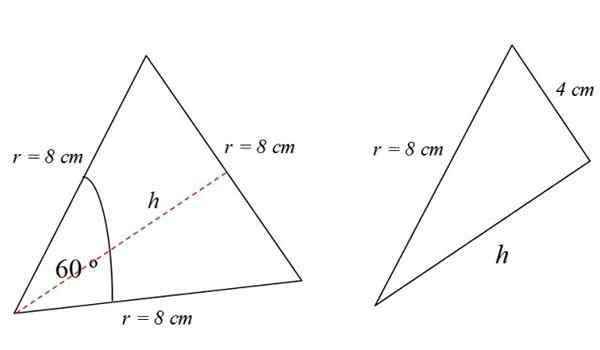
Di segitiga kanan, Teorema Pythagoras terpenuhi, oleh karena itu:

Karena Anda memiliki ketinggian segitiga, baik persegi panjang dan sisi, luasnya dihitung:

KE _{segi tiga} = (1/2) basis x tinggi = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Langkah 3: Perhitungan area yang diarsir

Cukup untuk mengurangi area utama (dari sektor melingkar) dari area minor (yaitu segitiga sama sisi): a _{wilayah teduh} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Perhitungan perimeter daerah yang diarsir

Perimeter yang dicari adalah jumlah dari sisi bujursangkar 8 cm dan busur lingkar AB.  Namun, keliling lengkap menggantikan 360 º, oleh karena itu busur bahwa Subthes 60 º adalah bagian keenam dari panjang penuh, yang kita tahu adalah 2.π.A:

Dapat melayani Anda: Fungsi Tumbuh: Cara Mengidentifikasi, Contoh, Latihan

AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Mengganti, perimeter wilayah teduh adalah:

P = 8 cm + 8.38 cm = 16.38 cm.

Aplikasi

Perimeter, seperti daerah ini, adalah konsep yang sangat penting dalam geometri dan dengan banyak aplikasi dalam kehidupan sehari -hari.

Seniman, desainer, arsitek, insinyur, dan banyak orang lainnya menggunakan perimeter sambil mengembangkan pekerjaan mereka, terutama dari lingkaran, karena bentuk bundar ada di mana -mana: dari iklan, melalui makanan hingga mesin.

Lingkar dan lingkaran adalah di antara geometri yang paling banyak digunakan. Sumber: Pixabay.

Untuk mengetahui secara langsung panjang lingkaran, itu cukup untuk membungkusnya dengan benang atau string, lalu rentangkan utas ini dan ukur dengan pita pita. Alternatif lainnya adalah mengukur jari -jari atau diameter lingkaran dan menggunakan beberapa rumus yang dijelaskan di atas.

Dalam pekerjaan sehari -hari, konsep perimeter digunakan saat:

-Cetakan yang sesuai dipilih untuk pizza atau ukuran kue tertentu.

-Jalan perkotaan akan dirancang, dengan menghitung ukuran redoma di mana mobil dapat beralih untuk mengubah makna.

-Kita tahu bahwa Bumi berkisar di sekitar matahari dalam orbit yang kira -kira melingkar -dalam kenyataan bahwa orbit planet bersifat elips, menurut hukum Kepler -tetapi kelilingnya adalah pendekatan yang sangat baik untuk sebagian besar planet planet.

-Ukuran cincin atau cincin yang sesuai yang akan dibeli di toko online dipilih.

-Kami memilih kunci ukuran yang tepat untuk melonggarkan kacang.

Dan masih banyak lagi.

https: // youtu.BE/CR8XJRYL5TK

Referensi

1. Tutorial matematika gratis. Area dan perimeter lingkaran - kalkulator geometri. Dipulihkan dari: analisis.com.
2. Referensi Terbuka Matematika. Keliling, perimeter lingkaran. Pulih dari: mathpenref.com.
3. Institut Monterey. Perimeter dan Area. Pulih dari: montereyinstitute.org.
4. Ilmu pengetahuan. Bagaimana menemukan perimeter lingkaran. Pulih dari: ilmuwan.com.
5. Wikipedia. Lingkar. Diperoleh dari: di.Wikipedia.org.