Y = 3sen (4x) periode fungsi

Dia Y = 3sen (4x) periode fungsi 2π/4 = π/2. Untuk memahami dengan jelas alasan pernyataan ini, definisi periode fungsi dan periode fungsi sen (x) harus diketahui; Sedikit tentang grafik fungsi juga akan berguna.

Fungsi trigonometri, seperti sinus dan cosinus (sen (x) dan cos (x)), sangat berguna baik dalam matematika maupun teknik.

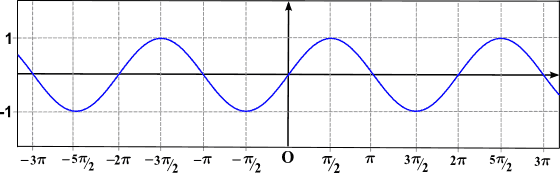
Periode kata menyebutkan pengulangan suatu peristiwa, jadi untuk mengatakan bahwa suatu fungsi secara periodik setara dengan mengatakan "grafiknya adalah pengulangan sepotong kurva". Seperti dapat dilihat pada gambar sebelumnya, fungsi sen (x) bersifat periodik.

Fungsi Berkala

Fungsi f (x) dikatakan periodik jika ada nilai nyata p ≠ 0 sedemikian rupa sehingga f (x+p) = f (x) untuk semua x dalam domain fungsi. Dalam hal ini, periode fungsi adalah p.

Secara umum disebut periode fungsi pada bilangan real positif terendah P yang memenuhi definisi.

Seperti dapat dilihat pada grafik sebelumnya, fungsi sen (x) bersifat periodik dan periodenya adalah 2π (fungsi kosinus juga periodik, dengan periode yang sama dengan 2π).

Perubahan dalam grafik suatu fungsi

Biarkan f (x) menjadi fungsi yang grafiknya diketahui, dan menjadi konstanta positif. Apa yang terjadi pada grafik f (x) jika dikalikan f (x) dengan c? Dengan kata lain, bagaimana grafik c*f (x) dan f (cx)?

Grafik c*f (x)

Dengan mengalikan fungsi, secara eksternal, dengan konstanta positif, grafik f (x) mengalami perubahan dalam nilai output; Artinya, perubahannya secara vertikal dan dua kasus dapat diambil:

- Jika C> 1, maka grafik mengalami peregangan vertikal dengan faktor C.

- Ya 0

F Graph (CX)

Ketika argumen fungsi dikalikan dengan konstanta, grafik f (x) mengalami perubahan dalam nilai input; Artinya, perubahannya secara horizontal dan, seperti sebelumnya, dua kasus dapat diambil:

- Jika c> 1, maka grafik menderita kompresi horizontal dengan faktor 1/c.

- Ya 0

Y = 3sen (4x) periode fungsi

Perlu dicatat bahwa dalam fungsi f (x) = 3se (4x) Ada dua konstanta yang mengubah grafik fungsi sinus: satu mengalikan eksternal dan lainnya dengan cara internal.

3 yang berada di luar fungsi sinus adalah untuk memperluas fungsi secara vertikal dengan faktor 3. Ini menyiratkan bahwa grafik fungsi 3sen (x) akan berada di antara nilai -3 dan 3.

4 yang berada dalam fungsi sinus membuat grafik fungsi kompresi horizontal untuk faktor 1/4.

Di sisi lain, periode fungsi diukur secara horizontal. Karena periode fungsi sen (x) adalah 2π, ketika mempertimbangkan dosa (4x) ukuran periode akan berubah.

Untuk mengetahui berapa periode y = 3sen (4x) cukup kalikan periode fungsi sen (x) dengan 1/4 (faktor kompresi).

Dengan kata lain, periode fungsi y = 3sen (4x) adalah 2π/4 = π/2, seperti yang dapat dilihat dalam grafik terakhir.