Pesawat Cartesian

Apa pesawat cartesian?

Dia Pesawat Cartesian Ini terdiri dari sepasang garis lurus yang tegak lurus satu sama lain dan yang berpotongan pada satu titik. Salah satu garis adalah vertikal dan yang lainnya horizontal, mengambil ke titik persimpangan sebagai asal sistem.

Tujuannya adalah untuk dengan mudah menemukan titik datar apa pun melalui sepasang nilai: koordinat. Untuk melakukan ini, pada masing -masing baris skala dengan bilangan bulat dibangun, yang positif ditulis dalam satu arah dan negatif di yang lain, seperti yang ditunjukkan pada gambar berikut:

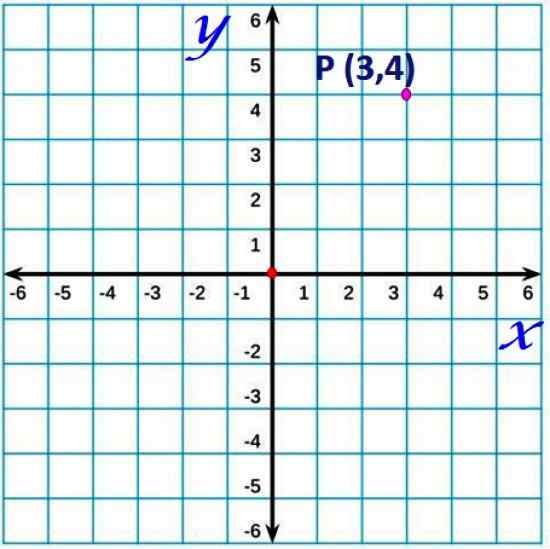
Gambar 1. Titik di pesawat Cartesian. Sumber: f. Zapata.

Dengan konvensi, sumbu horizontal biasanya disebut x dan sumbu vertikal sebagai sumbu dan.

Titik setiap pesawat akan memiliki koordinat yang ditentukan oleh pasangan yang tertib (X, y). Misalnya, titik p koordinat (3,4), terletak 3 unit di sebelah kanan asal dan 4 unit ke atas, pada gambar atas. Ini mirip dengan peta, yang menunjukkan garis lintang dan panjang lokasi tertentu.

Karena dua koordinat diperlukan, dikatakan bahwa pesawat tersebut dua dimensi, tetapi konsepnya mudah diperluas ke tiga dimensi, menambahkan sumbu yang lebih koordinat, yang biasanya dilambangkan sebagai sumbu z z. Dalam hal ini, koordinat terbentuk (X dan z).

Pesawat Cartesian menerima namanya dari ilmuwan Prancis René Descartes (1596-1650), yang memformalkannya dalam karyanya Pidato metode dari 1637, meskipun ada sejarah dalam karya-karya Apollonius dari Perga (262-190 ac), ahli matematika yang menemukan kurva kerucut: keliling, elips, perumpamaan dan hiperbola.

Dapat melayani Anda: Perbedaan kubus: Rumus, persamaan, contoh, latihan

Karakteristik bidang Cartesian

- Saat dia Sumbu x Sebagai Sumbu y Mereka memanjang secara tak terbatas di kedua ujungnya, dan berpotongan bersama -sama (pada sudut 90 derajat). Fitur ini disebut Orthogonality.

- Titik di mana kedua sumbu berpotongan dikenal sebagai titik asal atau nol.

- Sistem koordinat membagi pesawat menjadi empat wilayah yang disebut kuadran.

- Lokasi di bidang koordinat digambarkan sebagai pasangan yang dipesan.

- Setiap titik pada bidang Cartesian dikaitkan dengan koordinat x yang unik dan koordinat dan unik.

Elemen pesawat Cartesian

Elemen -elemen bidang Cartesian adalah sebagai berikut:

-Itu Garis numerik salah satu Koordinat sumbu x dan y, Jika itu pesawat. Sumbu Dan menerima nama sumbu dari ordinat, sedangkan sumbu X Itu adalah sumbu absissa. Ketika datang ke luar angkasa, maka sumbu ditambahkan z, mampu mewakili tinggi dan kedalaman.

-Dia asal, yang merupakan titik persimpangan sumbu.

-Itu kuadran, yang merupakan daerah yang ditentukan sumbu koordinat pada bidang dan dihitung dalam arah yang berlawanan dengan tangan jam, dimulai dengan kuadran pertama. Mereka didefinisikan sebagai berikut:

• Kuadran Pertama: Axes X Dan Dan positif.
• Kuadran Kedua: Sesuai dengan sumbu x negatif dan sumbu dan positif.
• Kuadran Ketiga: Memiliki kedua sumbu negatif.
• Kuadran Keempat: Dengan sumbu x positif dan sumbu dan negatif.

Secara umum, kuadran dilambangkan dalam angka Romawi, seperti ini:

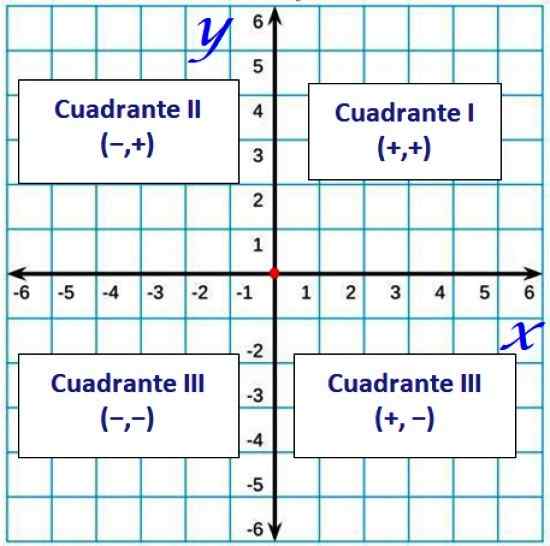Gambar 2. Cuadrants di Pesawat Cartesian. Sumber: f. Zapata.

Dipesan pasangan dan jarak antara dua titik

Pasangan yang dipesan adalah koordinat dari setiap titik, di mana koordinat x selalu ditempatkan terlebih dahulu, seperti pada contoh Gambar 1. Koordinat (3,4) dari titik P menunjukkan itu x = 3 Dan y = 4.

Dalam gambar lain di bawah ini, titik p milik kuadran IV dan memiliki koordinat (2; −1.5). Perhatikan bahwa dengan memproyeksikan garis dari sumbu koordinat ke titik p membentuk persegi panjang. Inilah alasan mengapa koordinat Cartesian juga disebut Koordinat persegi panjang.

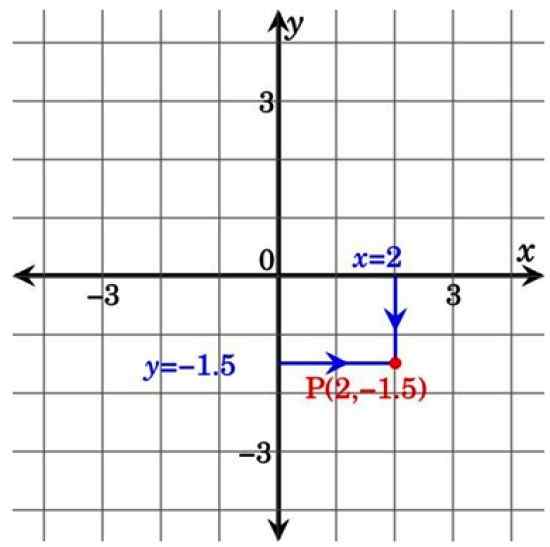Gambar 3. Tunjuk di pesawat Cartesian. Sumber: Wikimedia Commons.

Aplikasi Pesawat Cartesian

Pesawat Cartesian memiliki banyak aplikasi di banyak bidang. Awalnya, Descartes memperkenalkannya ke grafik kurva kurva di bidang, itulah sebabnya dianggap sebagai bapak geometri analitik.

Dapat melayani Anda: Produk Cruz

Namun, penggunaannya meluas untuk membuat grafik semua jenis hubungan dan fungsi, seperti:

-Ikuti lintasan tubuh dengan gerakan parabola, melingkar atau lengkung pada umumnya.

-Secara grafis menentukan cara di mana dua variabel terkait melalui fungsi.

-Temukan titik di tanah datar untuk memfasilitasi pengukuran di atasnya.

Referensi

1. Matematika itu menyenangkan. Koordinat Cartesian. Pulih dari: mathsisfun.com/data/cartesian-koordinat.
2. Pesawat Cartesian. Diperoleh dari: DL.Uncw.Edu.