Sifat poligon biasa, elemen, sudut, contoh

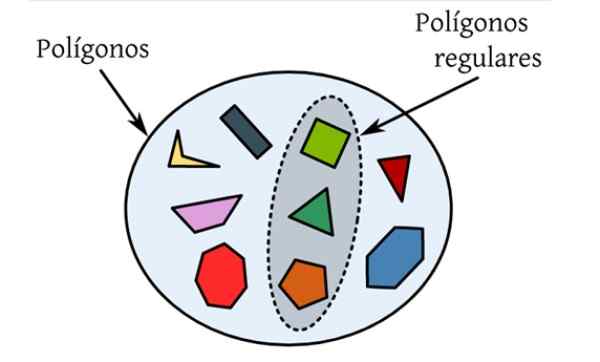
Itu Poligon biasa Mereka adalah mereka yang memiliki semua sisi dan sudut internal mereka yang setara. Pada gambar berikut ada satu set poligon yang berbeda, yang merupakan angka datar yang dibatasi oleh kurva tertutup dan hanya yang disorot memenuhi syarat untuk menjadi biasa.

Misalnya, segitiga sama sisi adalah poligon biasa, karena ketiga sisinya mengukur sama, serta sudut internalnya, yang masing -masing bernilai 60 º masing -masing.

Gambar 1. Poligon biasa adalah mereka yang sisi dan sudut internalnya sama, seperti segitiga sama sisi dan persegi. Sumber: Wikimedia Commons.

Kotak adalah segi empat dengan empat sisi dengan ukuran yang sama dan yang sudut internalnya 90º. Diikuti oleh Pentagon biasa, dengan lima sisi dengan ukuran yang sama dan lima sudut internal masing -masing 108º.

Ketika poligon biasa, kata ini ditambahkan ke nama istimewa, sehingga kami memiliki segi enam biasa, heptagon biasa dan sebagainya.

[TOC]

Sifat poligon biasa

Sifat terpenting dari poligon biasa dapat diringkas sebagai berikut:

-Sisi mengukur sama, oleh karena itu mereka ekuilateral.

-Adalah Equiagular, Nah, semua sudut internalnya memiliki ukuran yang sama.

-Mereka selalu dapat mendaftar di lingkar, yang berarti bahwa mereka sangat cocok menjadi satu, yang disebut Lingkar terbatas.

-Untuk poligon reguler dari sisi N, ukuran sudut dalam α adalah:

α = [180 (n-2)]/n

-N-3)/2 diagonal dapat diambil dari simpul poligon, baik secara teratur atau tidak.

-Jumlah dari sudut eksterior Itu sama dengan 360º.

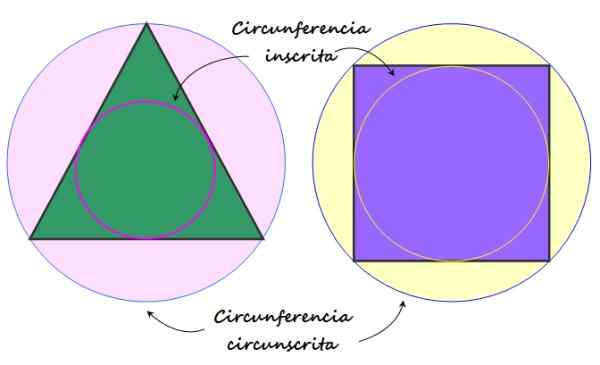Gambar 2. Lingkar Terdaftar dan Lingkar Dibatasi pada Poligon Reguler. Sumber: f. Zapata.

Elemen poligon biasa

Kemudian kami menyajikan elemen utama poligon biasa, divisualisasikan pada gambar yang lebih rendah.

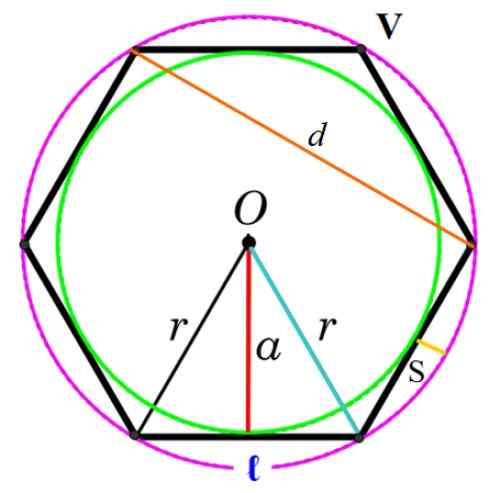Gambar 3. Elemen poligon biasa. Sumber: f. Zapata.

Puncak

Titik umum yang memiliki dua sisi berturut -turut, dilambangkan sebagai v pada gambar.

Samping

Itu adalah segmen yang bergabung dengan dua simpul berturut -turut dari poligon dan dilambangkan sebagai ℓ atau l.

Diagonal

Segmen yang bergabung dengan dua simpul poligon non -berturut -turut, dalam gambar itu dilambangkan sebagai D.

Tengah

Ini adalah pusat umum dari lingkar terdaftar dan keliling yang dibatasi, dilambangkan dengan surat atau. Itu juga dapat dilihat sebagai satu -satunya titik yang menyatu dari simpul dan titik tengah di setiap sisi.

Radio

Itu adalah radio R dari lingkar yang dibatasi dan bertepatan dengan jarak antara O dan verteks.

Itu dapat melayani Anda: aksioma probabilitas: jenis, penjelasan, contoh, latihan

Apothem

Itu disebut apothem ke jari -jari keliling yang tertulis dalam poligon, diwakili dalam gambar dengan huruf ke. Apothem tegak lurus terhadap samping dan menyatukan ini dengan pusat O (segmen merah pada Gambar 3).

Mengetahui jari -jari R dan panjang sisi, apothem dihitung oleh:

Karena, pada dasarnya, apothem adalah salah satu kategori segitiga persegi panjang (lihat Gambar 3), cateto lainnya adalah nilai ℓ/2 (setengah dari satu sisi) dan hipotenus di radio R dari poligon.

Ketika teorema Pythagoras diterapkan pada segitiga tersebut, persamaan ini diperoleh, yang valid tidak hanya untuk segi enam, tetapi untuk poligon biasa apa pun.

Sudut tengah

Itu adalah sudut yang simpulnya bertepatan dengan pusat atau sisi yang merupakan segmen yang menyatukan pusat dengan dua simpul berturut -turut. Ukurannya dalam derajat seksasimal adalah 360º/n, di mana N Itu adalah jumlah sisi poligon.

Sagita

Ini adalah perbedaan antara jari -jari poligon dan apothem (lihat Gambar 3). Menunjukkan sagita sebagai s:

S = r - a

Perimeter dan Area

Perimeter

Mudah dihitung dengan menambahkan panjang sisi. Karena sisi mana pun memiliki panjang yang sama dan ada sisi N, perimeter P dinyatakan sebagai:

P = n.L

Daerah

Dalam poligon reguler, area A diberikan oleh produk antara semi-perimeter (setengah dari perimeter) dan panjang apothem ke.

A = p.A /2

Karena perimeter tergantung pada jumlah sisi n, ternyata:

A = (nl).A /2

Dua poligon biasa dapat memiliki perimeter yang sama bahkan jika mereka tidak memiliki jumlah sisi yang sama, karena kemudian akan tergantung pada panjang sisi.

Dalam Buku V dari Anda Koleksi, Pappus matematikawan dari Alexandria (290-350), yang terakhir dari matematika Yunani agung zaman kuno, menunjukkan bahwa di antara semua poligon reguler dengan perimeter yang sama, yang dengan area terbesar adalah satu dengan jumlah sisi terbesar yang terbesar dari sisi terbesar yang terbesar dari sisi terbesar terbesar terbesar terbesar terbesar terbesar terbesar terbesar terbesar terbesar terbesar terbesar terbesar.

Sudut

Gambar 4 menunjukkan sudut yang relevan dalam poligon biasa, dilambangkan dengan huruf -huruf Yunani α, β dan γ.

Sudut tengah

Sebelumnya kami menyebutkan sudut tengah, di antara elemen -elemen poligon biasa, itu adalah sudut yang simpulnya berada di tengah poligon dan sisi -sisinya adalah segmen yang menyatukan pusat dengan dua simpul berturut -turut.

Untuk menghitung ukuran sudut pusat α, 360º dibagi dengan N, jumlah sisi. Atau 2π radian antara N:

Dapat melayani Anda: fungsi suntikan: apa yang terdiri dari, untuk apa dan contohnya

α = 360º/n

Setara dengan radian dengan:

α = 2π /n

Sudut internal atau sudut dalam

Pada Gambar 4 sudut internal β adalah yang verteks bertepatan dengan salah satu gambar dan sisinya juga merupakan sisi dari gambar. Itu dihitung dalam derajat seksasimal dengan:

β = [180 (n-2)]/n

Atau dalam radian menggunakan:

β = [π (n-2)]/n

Sudut eksternal

Mereka dilambangkan dengan huruf Yunani γ. Pada gambar itu diamati bahwa γ + β = 180º. Karena itu:

γ = 180º - β

Jumlah semua sudut eksternal ke poligon biasa adalah 360º.

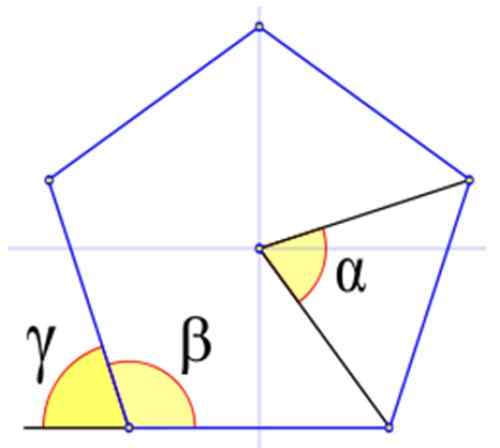Gambar 4. Sudut dalam poligon biasa, dalam contoh ini pentagon biasa. Sumber: Wikimedia Commons.

Contoh poligon biasa

Di bawah ini kami memiliki 8 poligon reguler pertama. Kami mengamati bahwa ketika jumlah sisi meningkat, poligon menjadi semakin banyak keliling di mana mereka terdaftar.

Kita dapat membayangkan bahwa membuat panjang sisi semakin kecil, dan meningkatkan jumlahnya, kita mendapatkan keliling.

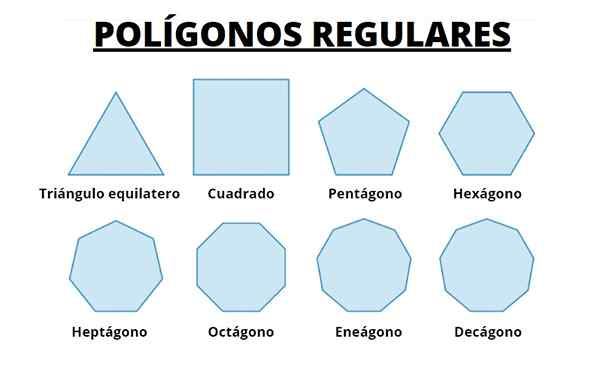Gambar 5. Delapan poligon reguler pertama. Sumber: Wikimedia Commons.

- Poligon biasa dalam kehidupan dan alam sehari -hari

Poligon biasa ditemukan di mana -mana dalam kehidupan sehari -hari dan bahkan di alam. Mari kita lihat beberapa contoh:

Sinyal lalu lintas

Di papan tanda kita melihat di jalan raya dan jalan -jalan berlimpah poligon biasa seperti segitiga sama sisi, persegi dan belah ketupat. Pada Gambar 6 kita melihat sinyal sinyal berbentuk tinggi.

Gambar 5.- Sinyal lalu lintas dengan bentuk segi delapan. Sumber: Pixabay.

Mebel

Potongan furnitur yang tak terhitung banyaknya persegi misalnya, sebagai sosok geometris yang khas, serta banyak meja, kursi, dan bank adalah persegi. Paralelepiped umumnya kotak dengan sisi berbentuk persegi panjang (yang bukan poligon biasa), tetapi mereka juga dapat membuat persegi.

Arsitektur dan Konstruksi

Ubin atau ubin lantai dan dinding, baik di rumah maupun di jalanan, sering memiliki bentuk poligon biasa.

Tesel adalah permukaan yang sepenuhnya ditutupi dengan ubin yang memiliki angka geometris yang beragam. Dengan segitiga, kotak dan segi enam dapat dibuat tesselves biasa, yang hanya menggunakan satu jenis sosok tunggal untuk melapisi dengan sempurna, tanpa ruang kosong (lihat Gambar 6).

Juga bangunan menggunakan poligon biasa dalam elemen seperti jendela dan dekorasi.

Gambar 6. Ubin persegi. Sumber: Pixabay.

- Hexagon biasa di alam

Yang mengejutkan, segi enam biasa adalah poligon yang sering muncul di alam.

Dapat melayani Anda: distribusi diskrit

Sarang lebah yang dibuat oleh lebah untuk menyimpan madu memiliki bentuk yang sangat perkiraan untuk segi enam biasa. Seperti yang diamati oleh pappus Alexandria, dengan cara ini lebah mengoptimalkan ruang untuk menghemat madu sebanyak mungkin.

Dan ada juga segi enam biasa dalam cangkang kura -kura dan kepingan salju, yang juga mengadopsi berbagai bentuk geometris yang sangat indah.

Olahraga diselesaikan

Hexagon biasa adalah bagian dari setengah lingkaran radius 6 cm, seperti yang ditunjukkan pada gambar. Berapa nilai area teduh?

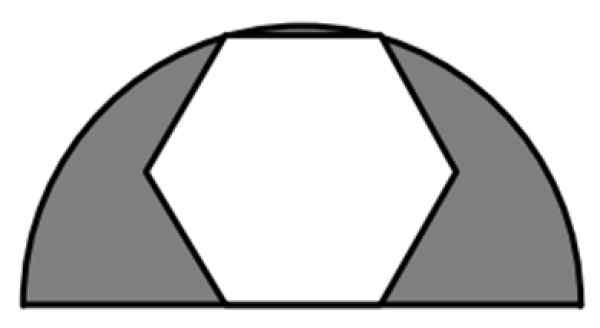Gambar 7. A regular hexagon registered in a semicircle. Sumber: f. Zapata.

Larutan

Area yang diarsir adalah perbedaan antara area setengah lingkaran radius r = 6 cm dan area heksagon penuh, poligon 6 -sided reguler. Jadi kita akan membutuhkan formula untuk area masing -masing angka ini.

Area setengah lingkaran

KE₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Area Hexagon biasa

Rumus untuk menghitung area poligon biasa adalah:

A = p.A /2

Di mana P Itu adalah perimeter dan ke Itu adalah apothem. Karena perimeter adalah jumlah sisi, kita akan membutuhkan nilai dari ini. Untuk segi enam biasa:

P = 6ℓ

Karena itu:

A = 6ℓa /2

Untuk menemukan nilai sisi ℓ perlu membangun angka tambahan, yang akan kami jelaskan di bawah ini:

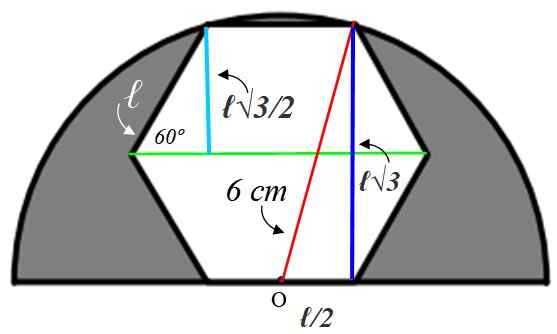
Mari kita mulai dengan segitiga persegi panjang kecil ke kiri, yang hipotenuse adalah ℓ. Sudut internal segi enam layak:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º

Jari -jari yang telah kita gambar di bisecta hijau sudut ini, oleh karena itu sudut akut dari segitiga kecil adalah 60º. Dengan informasi yang diberikan, segitiga ini diselesaikan, menemukan sisi biru muda, yang mengukur sama dengan apothem:

Cateto yang berlawanan = a = ℓ x sin 60º = ℓ√3 / 2 cm

Nilai ini adalah dua kali kaki biru gelap dari segitiga besar ke kanan, tetapi dari segitiga itu kita tahu bahwa hipotenuse berukuran 6 cm karena itu adalah jari -jari setengah lingkaran. Cateto yang tersisa (di bawah) bernilai ℓ/2 sejak titik atau di tengah samping.

Karena sudut internal segitiga ini tidak diketahui, kita dapat meningkatkan teorema Pythagoras untuknya:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Dengan nilai ini apothem dihitung:

a = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Sebutkan a₂ ke area segi enam biasa:

= 28. 8 cm²

Area sosok yang teduh

KE₁ - KE₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Referensi

1. Baldor, a. 1973. Geometri dan Trigonometri. Editorial Budaya Amerika Tengah.
2. Nikmati matematika. Tesel. Pulih dari: nikmatiMaticaticas.com.
3. DAN. KE. 2003. Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
4. Hexagon di alam. Pulih dari: malvargamath.WordPress.com.
5. Jiménez, r. 2010. Matematika II. Geometri dan Trigonometri. Edisi kedua. Prentice Hall.
6. Poligon biasa. Pulih dari: sobat.rekayasa.USAC.Edu.GT.
7. Wikipedia. Apothem. Pulih dari: is.Wikipedia.org.