Riwayat Prinsip Paskah, Aplikasi, Contoh

Dia Prinsip Pascal, o Hukum Pascal, menetapkan bahwa perubahan tekanan cairan yang terbatas pada salah satu titiknya ditransmisikan tanpa perubahan ke semua titik lain dalam cairan.

Prinsip ini ditemukan oleh ilmuwan Prancis Blaise Pascal (1623 - 1662). Karena pentingnya kontribusi yang dibuat oleh Pascal untuk sains, unit tekanan dalam sistem internasional telah ditunjuk untuk menghormatinya.

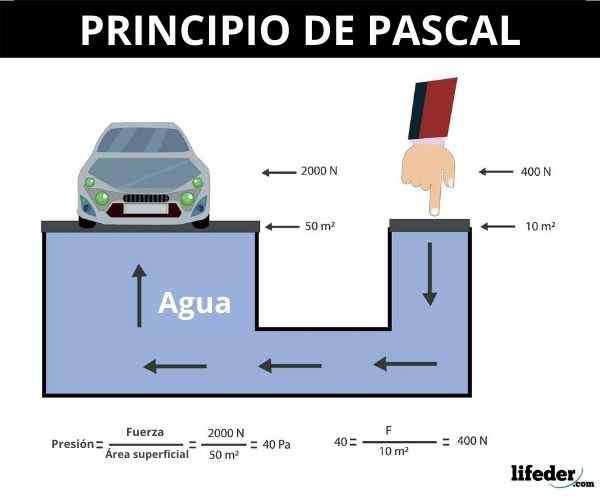
Karena tekanan didefinisikan sebagai hasil bagi antara gaya tegak lurus terhadap area antara luasnya, 1 pascal (PA) sama dengan 1 newton / m².

[TOC]

Sejarah

Untuk memverifikasi prinsipnya, Pascal menyusun demonstrasi yang agak luar biasa. Dia mengambil bola berlubang dan menusuk di beberapa tempat, meletakkan topi di semua lubang kecuali dalam satu, yang dia mengisinya dengan air. Dalam hal ini ia meletakkan jarum suntik yang dilengkapi dengan plunger.

Dengan cukup meningkatkan tekanan pada plunger, tutup ditembak pada waktu yang sama, karena tekanan ditransmisikan secara merata ke semua titik cairan dan di semua arah, sehingga menunjukkan hukum Pascal.

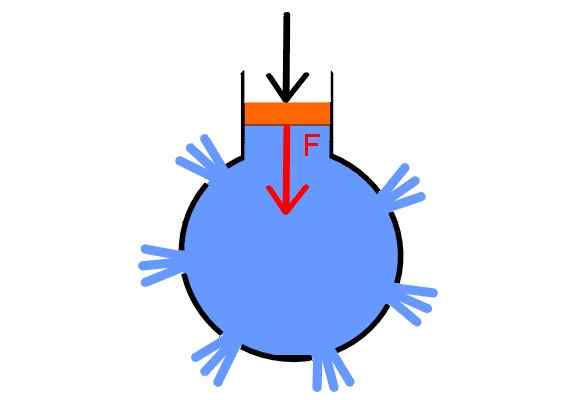Syringe Pascal. Sumber: Wikimedia Commons.

Blaise Pascal memiliki kehidupan yang singkat, ditandai oleh penyakit ini. Jangkauan pikirannya yang luar biasa membawanya untuk menyelidiki dalam berbagai aspek alam dan filsafat. Kontribusinya tidak terbatas untuk mempelajari perilaku cairan, Pascal juga merupakan pelopor komputasi.

Dan pada usia 19, Pascal menciptakan kalkulator mekanis bagi ayahnya untuk menggunakannya dalam pekerjaannya dalam sistem pajak Prancis: The Pascalina.

Juga, bersama dengan teman dan koleganya, matematikawan hebat Pierre dari Fermat, membentuk teori probabilitas, sangat diperlukan dalam fisika dan statistik. Pascal meninggal di Paris, pada usia 39 tahun.

Penjelasan Prinsip Pascal

Eksperimen berikutnya cukup sederhana: tabung U diisi dengan air dan tutup ditempatkan di setiap ujung yang dapat meluncur dengan lancar dan mudah, sebagai piston. Ini adalah tekanan terhadap piston kiri sedikit tenggelam dan diamati bahwa yang di kanan naik, didorong oleh cairan (gambar bawah).

Dapat melayani Anda: Andromeda: penemuan, asal, karakteristik, struktur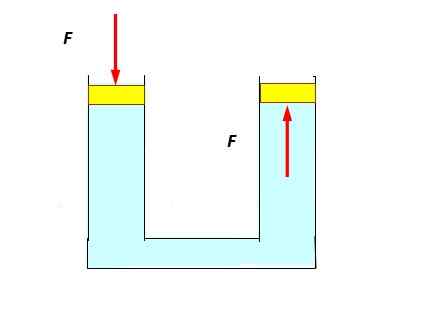Penerapan Prinsip Pascal. Sumber: Made sendiri.

Ini terjadi karena tekanan ditransmisikan tanpa penurunan ke titik penuh cairan, termasuk yang bersentuhan dengan piston kanan.

Cairan seperti air atau minyak tidak dapat dimampatkan tetapi pada saat yang sama molekul memiliki cukup kebebasan bergerak, yang memungkinkan tekanan didistribusikan pada piston kanan.

Berkat ini, piston kanan menerima kekuatan yang persis sama dalam besarnya dan arah yang diterapkan pada kiri, tetapi dari arah yang berlawanan.

Tekanan dalam cairan statis tidak tergantung pada bentuk wadah. Akan segera ditunjukkan bahwa tekanan bervariasi secara linear dengan kedalaman dan prinsip Pascal adalah konsekuensi dari ini.

Perubahan tekanan pada titik mana pun, membuat tekanan pada titik lain mengubah dalam jumlah yang sama. Kalau tidak, akan ada tekanan ekstra yang akan mengalir cairan.

Hubungan antara tekanan dan kedalaman

Cairan istirahat memberikan kekuatan pada dinding wadah yang berisi dan juga pada permukaan objek apa pun yang terendam di dalamnya. Dalam percobaan jarum suntik Pascal terlihat bahwa percikan air keluar tegak lurus Ke bola.

Cairan mendistribusikan gaya yang tegak lurus pada permukaan tempat ia bertindak, sehingga lebih mudah untuk memperkenalkan konsep tekanan rata -rata P_M sebagai gaya tegak lurus yang diberikan F_⊥ Menurut area KE, yang unitnya adalah Pascal:

P_M = F_⊥ / KE

Tekanan meningkat dengan kedalaman. Anda dapat melihat sebagian kecil cairan keseimbangan statis dan menerapkan hukum kedua Newton:

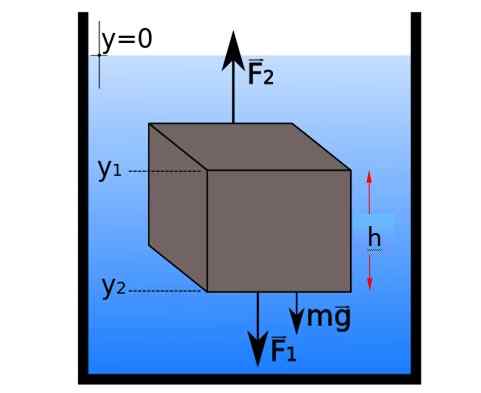Diagram tubuh bebas dari sebagian kecil keseimbangan statis dengan berbentuk kubus. Sumber: E-XUAO [CC BY-SA 4.0 (https: // createveCommons.Org/lisensi/by-sa/4.0)]

Kekuatan horizontal dibatalkan oleh pasangan, tetapi dalam arah vertikal kekuatan dikelompokkan sebagai berikut:

∑f_Dan = F₂ - F₁ - mg = 0 → F₂ - F₁ = mg

Mengekspresikan adonan dalam hal kepadatan ρ = massa /volume:

P₂.A- p₁.A = ρ X Volume X G

Volume bagian fluida adalah produk di x h:

Ini dapat melayani Anda: Hukum Kedua Termodinamika: Rumus, Persamaan, Contoh

KE.(P₂ - P₁) = ρ X a x h x g

ΔP = ρ.G.H   Teorema mendasar hidrostatik

Aplikasi

Sebuah backhoe memanfaatkan prinsip Pascal untuk mengangkat peso besar

Prinsip Pascal telah digunakan untuk membangun banyak perangkat yang melipatgandakan kekuatan dan memfasilitasi tugas -tugas seperti mengangkat peso, menginjak logam atau mengepung benda. Di antara mereka adalah:

-Pers hidrolik

-Sistem rem mobil

-Sekop mekanik dan lengan mekanik

-Kucing hidrolik

-Crane dan lift

Selanjutnya, mari kita lihat bagaimana prinsip Pascal membuat kekuatan kecil berubah menjadi kekuatan besar untuk melakukan semua pekerjaan ini. Pers hidrolik adalah contoh paling khas dan akan dianalisis di bawah ini.

Pers hidrolik

Untuk membangun pers hidrolik, perangkat yang sama dari gambar atas diambil, yaitu, wadah berbentuk U, yang sudah kita ketahui bahwa gaya yang sama ditransmisikan dari satu piston. Perbedaannya adalah ukuran piston dan inilah yang membuat perangkat berfungsi.

Gambar berikut menunjukkan prinsip pascal dalam aksi. Tekanannya sama di semua titik cairan, keduanya di piston kecil dan besar:

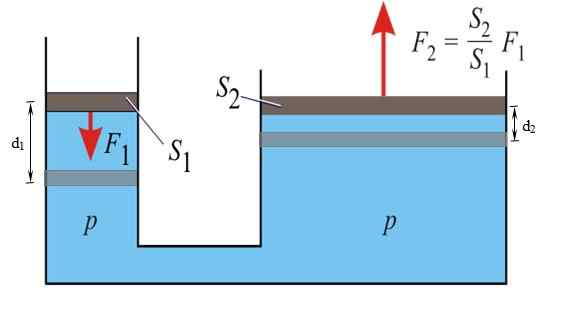Skema Pers Hidraulik. Sumber: Wikimedia Commons.

p = f₁ / S₁ = F₂ / S₂

Besarnya gaya yang ditransmisikan ke piston besar adalah:

F₂ = (S₂ / S₁). F₁

Seperti s₂ > S₁, menghasilkan f₂ > F₁, Oleh karena itu gaya keluar telah berlipat ganda dalam faktor yang diberikan dengan hasil bagi di antara area tersebut.

Contoh

Bagian ini menunjukkan contoh aplikasi.

Rem hidrolik

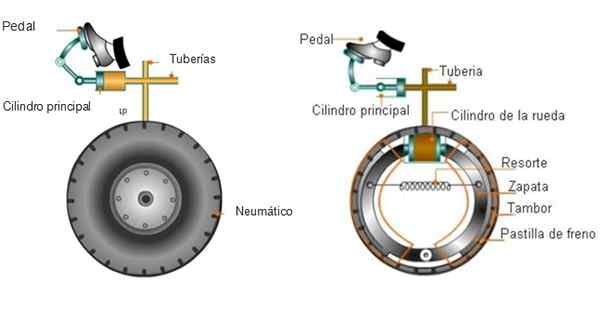
Rem Mobil Memanfaatkan Prinsip Pascal Melalui Cairan Hidrolik Yang Mengisi Beberapa Tabung Yang Terhubung Ke Roda. Saat Anda perlu berhenti, pengemudi menerapkan kekuatan dengan menindas pedal rem dan menghasilkan tekanan pada cairan.

Di ujung lain, tekanan mendorong bantalan rem ke drum atau cakram rem yang berputar bersama dengan roda (bukan dengan ban). Gesekan yang dihasilkan membuat disk berhenti, juga memperlambat roda.

Dapat melayani Anda: Gelombang Mekanik: Karakteristik, Properti, Rumus, JenisSistem Rem Hidrolik. Sumber: f. Zapata

Keuntungan mekanis dari pers hidrolik

Dalam pers hidrolik dari gambar yang lebih rendah, pekerjaan masuk harus sama dengan pekerjaan keluar selama gesekan tidak diperhitungkan.

Gaya input F₁ membuat piston menempuh jarak d₁ Saat turun, saat keluar dari kekuatan keluar F₂ Memungkinkan d₂ dari piston yang naik. Jika pekerjaan mekanis yang dilakukan oleh kedua kekuatan itu sama:

F₁.D₁ = F₂. D₂

Keuntungan mekanis M adalah hasil bagi antara besaran dari input dan gaya output:

M = f₂/F₁ = d₁/D₂

Dan seperti yang ditunjukkan pada bagian sebelumnya, itu juga dapat dinyatakan sebagai hasil bagi di antara area:

F₂/F₁ = S₂ / S₁

Tampaknya pekerjaan dilakukan secara gratis tetapi tidak benar -benar menciptakan energi dengan perangkat ini, karena keunggulan mekanis diperoleh dengan mengorbankan perpindahan piston kecil D₁.

Jadi untuk mengoptimalkan kinerja, sistem katup ditambahkan ke perangkat sedemikian rupa sehingga piston output dinaikkan berkat impuls pendek pada piston input.

Dengan cara ini operator pompa kucing hidrolik garasi beberapa kali untuk secara bertahap mengangkat kendaraan.

Olahraga diselesaikan

Dalam pers hidrolik Gambar 5, area piston adalah 0.5 inci persegi (piston kecil) dan 25 inci persegi (piston besar). Menemukan:

a) Keuntungan mekanis dari pers ini.

b) kekuatan yang diperlukan untuk mengangkat beban 1 ton.

c) Jarak di mana gaya masuk harus bertindak untuk mengangkat beban tersebut dalam 1 inci.

Ungkapkan semua hasil dalam unit sistem Inggris dan sistem internasional jika.

Larutan

A) Keuntungan mekanisnya adalah:

M = f₂/F₁ = S₂/S₁ = 25 in² / 0.5 in² = 50

b) 1 ton setara dengan 2000 lb-force. Kekuatan yang diperlukan adalah f₁:

F₁ = F₂ / M = 2000 lb-force / 50 = 40 lb- Force

Untuk mengekspresikan hasil dalam sistem internasional, faktor konversi berikut diperlukan:

1 lb-force = 4.448 n

Oleh karena itu besarnya F1 adalah 177.92 n.

C) M = d₁/D_{2 →} D₁ = M.D₂ = 50 x 1 in = 50 in

Faktor konversi yang diperlukan adalah: 1 in = 2.54 cm

D₁ = 127 cm = 1.27 m

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 417-450.
2. Fisika Perguruan Tinggi. Prinsip Pascal. Dipulihkan dari: opentextbc.Ac.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 4. Cairan dan termodinamika. Diedit oleh Douglas Figueroa (USB). 4 - 12.
4. Rex, a. 2011. Dasar -dasar fisika. Pearson. 246-255.
5. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit McGraw.301-320.