Konsep probabilitas frekuensi, bagaimana dihitung dan contoh

Itu Probabilitas frekuensi adalah Sub-definisi dalam studi probabilitas dan fenomenanya. Metode studinya sehubungan dengan peristiwa dan atribut, didasarkan pada sejumlah besar iterasi, sehingga mengamati masing -masing dalam jangka panjang atau bahkan pengulangan tak terbatas.

Misalnya, amplop gummitan berisi 5 karet dari masing -masing warna: biru, merah, hijau dan kuning. Anda ingin menentukan probabilitas bahwa setiap warna harus ditinggalkan setelah seleksi acak.

Sumber: Pexels

Sangat membosankan membayangkan mendapatkan karet, merekamnya, mengembalikannya, mengeluarkan karet dan mengulangi beberapa ratus atau beberapa ribu kali. Anda bahkan dapat mengamati perilaku setelah beberapa juta iterasi.

Tetapi sebaliknya menarik untuk ditemukan, bahwa setelah beberapa pengulangan probabilitas yang diharapkan 25% tidak sepenuhnya terpenuhi, setidaknya tidak untuk semua warna setelah 100 iterasi terjadi.

Di bawah pendekatan probabilitas frekuensi, alokasi nilai hanya akan melalui studi tentang banyak iterasi. Dengan cara ini proses harus dilakukan dan lebih disukai terdaftar dengan cara yang terkomputerisasi atau ditiru.

Ganda arus menolak probabilitas frekuensi, dengan alasan kurangnya empirisme dan keandalan dalam kriteria acak.

[TOC]

Bagaimana probabilitas frekuensi dihitung?

Saat memprogram percobaan dalam antarmuka apa pun yang mampu menawarkan iterasi acak murni, Anda dapat mulai mempelajari probabilitas frekuensi fenomena melalui tabel nilai.

Contoh sebelumnya dihargai dari pendekatan frekuensi:

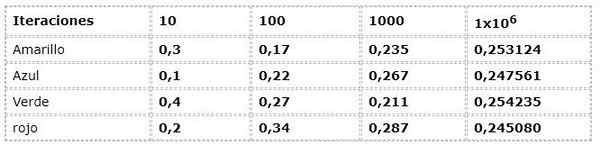
Data numerik sesuai dengan ekspresi:

N (a) = jumlah kejadian/ jumlah iterasi

Di mana n (a) mewakili frekuensi relatif dari acara "a"

"A" milik himpunan hasil yang mungkin atau ruang sampel Ω

Itu dapat melayani Anda: kelipatan 8: apa itu dan penjelasan

Ω: merah, hijau, biru, kuning

Ada dispersi yang cukup besar dalam iterasi pertama, ketika frekuensi dengan hingga 30% perbedaan diamati satu sama lain, yang merupakan fakta yang sangat tinggi untuk percobaan yang secara teoritis memiliki peristiwa dengan kemungkinan yang sama (Equiprobable).

Tetapi seiring dengan tumbuhnya iterasi, nilai -nilai tampak semakin banyak bagi yang disajikan oleh arus teoretis dan logis.

Hukum Angka Besar

Sebagai kesepakatan yang tidak terduga antara pendekatan teoretis dan frekuensi, hukum jumlah besar muncul. Di mana ditetapkan bahwa setelah sejumlah besar iterasi, nilai -nilai percobaan frekuensi mendekati nilai -nilai teoretis.

Dalam contoh Anda dapat melihat bagaimana nilai diperkirakan menjadi 0,250 saat iterasi tumbuh. Fenomena ini adalah dasar dalam kesimpulan dari banyak karya probabilistik.

Sumber: Pexels

Pendekatan probabilitas lainnya

Ada 2 teori atau pendekatan lain untuk gagasan probabilitas selain Probabilitas frekuensi.

Teori logis

Pendekatan Anda berorientasi pada logika fenomena deduktif. Dalam contoh sebelumnya probabilitas mendapatkan setiap warna ditutup. Dengan kata lain.

Teori subyektif

Didasarkan pada pengetahuan dan keyakinan sebelumnya yang dimiliki masing -masing individu tentang fenomena dan atribut. Pernyataan seperti "Itu selalu hujan di Pekan Suci " Mereka mematuhi pola peristiwa serupa yang telah terjadi sebelumnya.

Sejarah

Awal dari tanggal implementasinya dari abad kesembilan belas, ketika saya mengutipnya di beberapa karyanya di Cambridge England. Tetapi tidak sampai abad kedua puluh 2 matematika statistik berkembang dan membentuk Probabilitas frekuensi.

Dapat melayani Anda: persamaan polinomial

Salah satunya adalah Hans Reichenbach, yang mengembangkan karyanya dalam publikasi seperti "teori probabilitas" yang diterbitkan pada tahun 1949.

Yang lainnya adalah Richard von Mises, yang mengembangkan karyanya secara lebih menyeluruh melalui banyak publikasi dan mengusulkan untuk mempertimbangkan probabilitas sebagai ilmu matematika. Konsep ini baru dalam matematika dan akan menandai awal era pertumbuhan dalam studi tentang Probabilitas frekuensi.

Sebenarnya acara ini membuat satu -satunya perbedaan dengan kontribusi yang dibuat oleh generasi Venn, Counot dan Helm. Di mana probabilitas menjadi mitra seperti geometri dan mekanika.

< La teoría de las probabilidades trata con Fenomena besar dan peristiwa berulang. Masalah di mana peristiwa yang sama diulang berulang kali, atau sejumlah besar elemen seragam terlibat pada saat yang sama> Richard von Mises

Fenomena besar dan peristiwa berulang

Tiga jenis dapat diklasifikasikan:

• Fisika: Obdose pola alam di luar kondisi acak. Misalnya perilaku molekul suatu unsur dalam sampel.
• Peluang: Pertimbangan mendasarnya adalah keacakan, seperti dengan melepaskan dadu berulang kali.
• Statistik Biologis: Pilihan subjek uji sesuai dengan karakteristik dan atributnya.

Dalam teori, individu yang mengukur berperan dalam data probabilistik, karena pengetahuan dan pengalamannya yang mengartikulasikan nilai atau prediksi ini.

Dalam Probabilitas frekuensi Acara akan dianggap sebagai koleksi untuk diperlakukan, di mana individu tidak memainkan peran apa pun dalam perkiraan.

Atribut

Di setiap elemen, atribut terjadi, yang akan bervariasi sesuai dengan sifat ini. Misalnya, dalam jenis fenomena fisik, molekul air akan memiliki kecepatan yang berbeda.

Itu dapat melayani Anda: kriteria kesamaan triangulous

Dalam peluncuran dadu kita tahu ruang sampel Ω yang mewakili atribut percobaan.

Ω: 1, 2, 3, 4, 5, 6

Ada atribut lain seperti Ω_P  atau menjadi aneh Ω_yo

Ω_P : 2, 4, 6

Ω_yo : 1, 3, 5

Yang dapat didefinisikan sebagai atribut non -elemen.

Contoh

• Anda ingin menghitung frekuensi setiap jumlah yang mungkin dalam peluncuran dua dadu.

Untuk ini, percobaan diprogram di mana dua nilai acak antara [1, 6] ditambahkan di setiap iterasi.

Data dicatat dalam tabel dan tren dalam jumlah besar dipelajari.

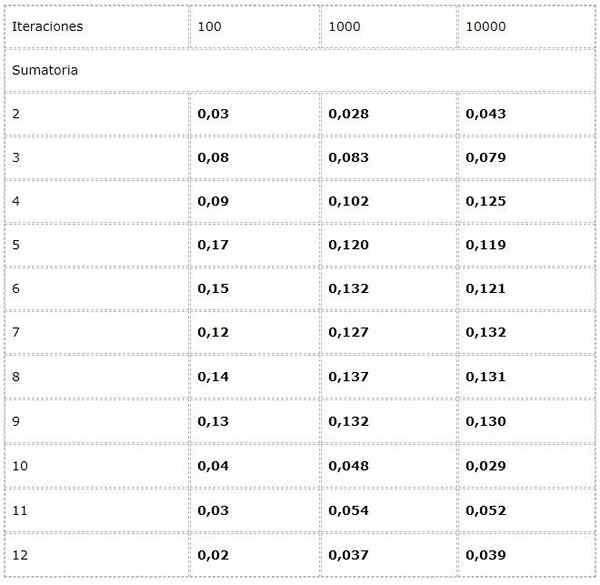
Diamati bahwa hasilnya dapat bervariasi secara signifikan antara iterasi. Namun, hukum jumlah besar dapat dilihat dalam konvergensi nyata yang disajikan dalam dua kolom terakhir.

Referensi

1. Statistik dan evaluasi bukti untuk ilmuwan forensik. Edisi kedua. Colin G.G. Aitken. Sekolah Matematika. Universitas Edinburgh, Inggris
2. Matematika untuk Ilmu Komputer. Eric Lehman. Google Inc.
   F Thomson Leighton Departemen Matematika dan Laboratorium Ilmu Komputer dan AI, Institut Teknologi Massachussetts; Teknologi Akamai
3. Guru Aritmatika, Volume 29. Dewan Nasional Guru Matematika, 1981. Universitas Michigan.
4. Teori Pembelajaran dan Pengajaran: Penelitian dalam Kognisi dan Instruksi / Diedit oleh Stephen R. Campbell dan Rina Zazkis. MABLX PUBLISHING 88 POST ROAD WEST, WESTPORT CT 06881
5. Bernoulli, J. (1987). ARS DINDECTANDI- 4ème Partie. Rouen: Irem.