Karakteristik pemrograman dinamis, contoh, kelebihan, kerugian

Itu Pemrograman Dinamis Ini adalah model algoritma yang memecahkan masalah kompleks dengan membaginya menjadi subproblem, menyimpan hasilnya untuk menghindari harus menghitung hasil tersebut.

Program ini digunakan ketika masalah dapat dibagi menjadi subproblem yang serupa, sehingga hasilnya dapat digunakan kembali. Untuk yang paling mayoritas, program ini digunakan untuk optimasi.

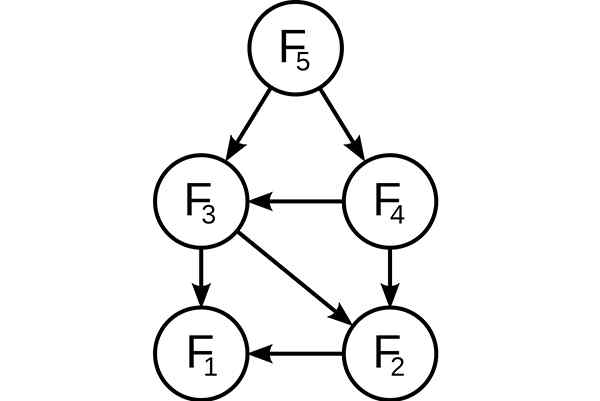
Pemrograman Dinamis. Subproblems yang ditumpangkan dalam suksesi Fibonacci. Sumber: Wikimedia Commons, AT: Pengguna: Dcoatzee, dilacak oleh Pengguna: Domain Stannered / Public

Sebelum memecahkan subproblema yang tersedia, algoritma dinamis akan mencoba memeriksa hasil subproblem yang sebelumnya diselesaikan sebelumnya. Solusi subproblem digabungkan untuk mencapai solusi terbaik.

Alih -alih menghitung subproblema yang sama berulang kali, solusi Anda dapat disimpan dalam beberapa memori, saat Anda pertama kali bertemu subproblema ini. Ketika muncul lagi selama solusi subproblem lain, solusi yang sudah disimpan dalam memori akan diambil.

Ini adalah ide yang bagus untuk memperbaiki waktu dengan memori, di mana saat menggunakan ruang tambahan Anda dapat meningkatkan waktu yang diperlukan untuk menemukan solusi.

[TOC]

Karakteristik pemrograman dinamis

Karakteristik penting berikut adalah masalah yang dapat diterapkan untuk pemrograman dinamis:

Substruktur optimal

Karakteristik ini mengungkapkan bahwa masalah optimisasi dapat diselesaikan dengan menggabungkan solusi optimal dari masalah sekunder yang membuatnya. Substruktur optimal ini dijelaskan dengan rekursi.

Misalnya, dalam grafik substruktur yang optimal akan disajikan pada rute terpendek yang beralih dari titik ke titik T:

Yaitu, pada rute terpendek ini r Anda dapat mengambil simpul menengah i. Jika R benar -benar rute terpendek, maka dapat dibagi menjadi subrutas R1 (dari S ke I) dan R2 (dari I ke T), sehingga pada gilirannya rute terpendek antara simpul yang sesuai.

Oleh karena itu, untuk menemukan rute terpendek, Anda dapat dengan mudah merumuskan solusi secara rekursif, yang merupakan algoritma Floyd-Warshall.

Subproblem yang ditumpangkan

Ruang subprob harus kecil. Yaitu, setiap algoritma rekursif yang memecahkan masalah harus menyelesaikan subproblem yang sama berulang kali, alih -alih menghasilkan subproblem baru.

Misalnya, untuk menghasilkan seri fibonacci, formulasi rekursif ini dapat dipertimbangkan: fn = f (n-1) + f (n-2), mengambil sebagai kasus dasar bahwa f1 = f2 = 1. Maka Anda harus: f33 = f32 + f31, dan f32 = f31 + f30.

Seperti yang dapat dilihat, F31 sedang diselesaikan dalam sub -season rekursif dari F33 dan F32. Meskipun jumlah total subprob sangat kecil, jika solusi rekursif diadopsi karena ini akan berakhir menyelesaikan masalah yang sama lagi dan lagi.

Dapat melayani Anda: 7 komponen sistem informasi

Ini diperhitungkan dengan pemrograman dinamis, jadi itu memecahkan setiap subproblem hanya sekali. Ini dapat dicapai dengan dua cara:

Pendekatan teratas

Jika solusi untuk masalah apa pun dapat diformulasikan secara rekursif menggunakan solusi subproblemnya, dan jika subproblem ini tumpang tindih, maka solusi untuk subproblem dapat dengan mudah dihafal atau disimpan dalam tabel dalam tabel.

Setiap kali solusi subproblema baru dicari, itu akan ditinjau dalam tabel jika sebelumnya diselesaikan. Dalam hal solusi disimpan, itu akan digunakan alih -alih menghitungnya lagi. Kalau tidak, subproblema akan diselesaikan, menyimpan solusi di tabel.

Pendekatan naik

Setelah solusi suatu masalah dirumuskan secara rekursif dalam hal subproblemnya, masalahnya dapat dicoba di atas: pertama -tama mereka akan mencoba menyelesaikan subproblem dan menggunakan solusi mereka untuk mencapai solusi dengan subproblem terbesar terbesar.

Ini juga biasanya dilakukan dalam bentuk tabel, menghasilkan solusi berulang untuk subproblem yang semakin besar dengan menggunakan solusi untuk subproblem kecil. Misalnya, jika nilai F31 dan F30 sudah diketahui, nilai F32 dapat dihitung secara langsung.

Perbandingan dengan teknik lain

Milik yang signifikan dari masalah yang dapat diselesaikan dengan pemrograman dinamis adalah bahwa ia harus memiliki subproblem yang tumpang tindih. Inilah yang membedakan pemrograman dinamis dari teknik membagi dan menaklukkan, di mana tidak perlu menyimpan nilai paling sederhana.

Ini mirip dengan rekursi, karena dengan menghitung kasus dasar, nilai akhir dapat ditentukan secara induktif. Pendekatan naik ini bekerja dengan baik ketika nilai baru hanya bergantung pada nilai yang dihitung sebelumnya.

Contoh

Langkah minimum untuk mencapai 1

Untuk semua bilangan bulat positif "e" Anda dapat melakukan salah satu dari tiga langkah berikut.

- Kurangi 1 dari angka. (E = E-1).

- Jika dapat dibagi dengan 2, dibagi dengan 2 (jika E%2 == 0, maka E = E/2).

- Jika dibagi dengan 3, dibagi dengan 3 (jika E%3 == 0, maka E = E/3).

Berdasarkan langkah -langkah sebelumnya, Anda harus menemukan jumlah minimum dari langkah -langkah ini untuk mengambil dan 1. Misalnya:

- Jika E = 1, hasilnya: 0.

- Jika E = 4, hasilnya: 2 (4/2 = 2/2 = 1).

- Ketika E = 7, Hasil: 3 (7-1 = 6/3 = 2/2 = 1).

Mendekati

Anda mungkin selalu berpikir tentang memilih langkah yang membuat N serendah mungkin dan melanjutkan seperti ini, sampai mencapai 1. Namun, dapat dilihat bahwa strategi ini tidak berhasil di sini.

Dapat melayani Anda: perangkat lunak komersial

Misalnya, jika E = 10, langkah-langkahnya adalah: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 langkah). Namun, cara optimal adalah: 10-1 = 9/3 = 3/3 = 1 (3 langkah). Oleh karena itu, semua langkah yang mungkin dapat dibuat untuk setiap nilai n harus dibuktikan, memilih jumlah minimum dari kemungkinan -kemungkinan ini.

Semuanya dimulai dengan rekursi: f (e) = 1 + min f (e-1), f (e/2), f (e/3) Jika e> 1, mengambil kasus dasar: f (1 ) = 0. Memiliki persamaan kekambuhan, Anda dapat mulai mengkode rekursi.

Namun, dapat diamati bahwa ia memiliki subproblem yang ditumpangkan. Selain itu, solusi optimal untuk input yang diberikan tergantung pada solusi optimal dari subproblemnya.

Seperti dalam menghafal, di mana solusi subproblem yang diselesaikan disimpan untuk menggunakannya nanti. Atau seperti dalam pemrograman dinamis, itu dimulai dari bawah, maju ke E yang diberikan. Selanjutnya, kedua kode:

Menghafal

Pemrograman ke atas dinamis

Keuntungan

Salah satu keuntungan utama menggunakan pemrograman dinamis adalah bahwa ia mempercepat pemrosesan, karena referensi yang sebelumnya dihitung digunakan. Seperti teknik pemrograman rekursif, ini mengurangi baris kode program.

Vorace Algoritmos vs Programming Dinamis

Algoritma rakus mirip dengan pemrograman dinamis dalam arti bahwa keduanya adalah alat untuk optimasi. Namun, algoritma Voraz mencari solusi optimal di setiap langkah lokal. Artinya, ia mencari pilihan serakah dengan harapan menemukan global optimal.

Oleh karena itu, algoritma yang rakus dapat membuat asumsi yang terlihat optimal pada waktu itu, tetapi itu menjadi mahal di masa depan dan tidak menjamin optimal global.

Di sisi lain, pemrograman dinamis menemukan solusi optimal untuk subproblem dan kemudian membuat pilihan berdasarkan informasi dengan menggabungkan hasil subproblem tersebut untuk benar -benar menemukan solusi yang paling optimal.

Kerugian

- Banyak memori yang diperlukan untuk menyimpan hasil yang dihitung dari setiap subproblem, tanpa dapat memastikan bahwa nilai yang tersimpan akan digunakan atau tidak.

- Berkali -kali, nilai output disimpan tanpa pernah digunakan dalam subproblem berikut selama eksekusi. Ini mengarah pada penggunaan memori yang tidak perlu.

- Dalam pemrograman dinamis, fungsi -fungsi itu disebut rekursif. Ini membuat memori baterai tetap terus meningkat.

Pemrograman rekursif vs dinamis

Jika Anda memiliki memori terbatas untuk menjalankan kode dan kecepatan pemrosesan tidak mengkhawatirkan, rekursif dapat digunakan. Misalnya, jika aplikasi seluler sedang dikembangkan, memori sangat terbatas untuk menjalankan aplikasi.

Dapat melayani Anda: Perangkat Campuran: Karakteristik dan Contoh

Jika program ini diinginkan untuk dieksekusi lebih cepat dan tidak ada batasan memori, lebih baik menggunakan pemrograman dinamis.

Aplikasi

Pemrograman dinamis adalah metode yang efektif untuk memecahkan masalah yang seharusnya tampak sangat sulit untuk dipecahkan dalam waktu yang wajar.

Algoritma berdasarkan paradigma pemrograman dinamis digunakan di banyak bidang sains, termasuk banyak contoh dalam kecerdasan buatan, dari resolusi masalah perencanaan hingga pengenalan suara.

Algoritma pemrograman dinamis

Pemrograman dinamis cukup efektif dan berfungsi dengan sangat baik untuk berbagai masalah. Banyak algoritma dapat dilihat sebagai aplikasi algoritma yang rakus, seperti:

- Seri Nomor Fibonacci.

- Hanoi Towers.

- Semua pasangan rute terpendek oleh Floyd-Warshall.

- Ransel.

- Pemrograman Proyek.

- Jalan terpendek oleh Dijkstra.

- Kontrol dan Kontrol Penerbangan Robotika.

- Masalah optimasi matematika.

- Waktu Bersama: Program pekerjaan untuk memaksimalkan penggunaan CPU.

Seri Nomor Fibonacci

Angka Fibonacci adalah angka yang ditemukan dalam urutan berikut: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144, dll.

Dalam terminologi matematika, suksesi fn angka fibonacci didefinisikan oleh rumus kekambuhan: f (n) = f (n -1) + f (n -2), di mana f (0) = 0 dan f (1) = 1.

Pendekatan teratas

Dalam contoh ini, matriks pencarian dengan semua nilai awal diinisialisasi dengan -1. Setiap kali solusi untuk subproblem diperlukan, pertama -tama akan dicari dalam matriks pencarian ini.

Jika ada nilai yang dihitung, maka nilai itu akan dikembalikan. Jika tidak, hasilnya akan dihitung untuk menyimpannya di matriks pencarian dan dengan demikian dapat menggunakannya kembali nanti.

Pendekatan naik

Dalam hal ini, untuk seri fibonacci yang sama, f (0), lalu f (1), f (2), f (3), dan sebagainya dihitung terlebih dahulu. Dengan demikian, solusi subproblem dari bawah akan dibangun.

Referensi

1. Vineet Choudhary (2020). Pengantar Pemrograman Dinamis. Orang dalam yang tidak berveloper.Diambil dari: pengembang.bersama.
2. Alex Allain (2020). Pemrograman dinamis di C++. Pemrograman C. Diambil dari: cprogrammming.com.
3. After Academy (2020). Ide pemrograman dinamis. Diambil dari: afteracademy.com.
4. Aniruddha Chaudhari (2019). Pemrograman dan Rekursi Dinamis | Berbeda. Tumpukan CSE. Diambil dari: csestack.org.
5. Kode Kode (2020). Untuk tutorial pemrograman dinamis. Diambil dari: codhef.com.
6. Programiz (2020). Pemrograman Dinamis. Diambil dari: Programiz.com.