Pemrograman linier untuk apa, model, pembatasan, aplikasi

Itu Pemrograman linier Ini adalah metode matematika yang berfungsi untuk mengoptimalkan (memaksimalkan atau meminimalkan sesuai kebutuhan) suatu fungsi yang variabelnya dapat dibatasi, selama fungsi dan pembatasan secara linier tergantung pada variabel.

Umumnya fungsi untuk mengoptimalkan situasi praktis, seperti perolehan produsen yang input, tenaga kerja, atau mesin terbatas.

Gambar 1. Pemrograman linier banyak digunakan untuk mengoptimalkan keuntungan. Sumber: Piqsels.

Salah satu kasus paling sederhana adalah fungsi linier untuk memaksimalkan, yang hanya tergantung pada dua variabel, disebut Variabel keputusan. Itu bisa terbentuk:

Z = k₁x + k₂Dan

Dengan k₁ dan k₂ konstanta. Fungsi ini dikenal sebagai Fungsi objektif. Tentu saja ada situasi yang pantas lebih dari dua variabel untuk studi mereka, menjadi lebih kompleks:

Z = k₁X₁ + k₂X₂ + k₃X₃ +.. .

Dan pembatasan juga dimodelkan secara matematis melalui sistem persamaan atau ketidaksetaraan, sama liniernya X Dan Dan.

Himpunan solusi dari sistem ini disebut solusi yang layak salah satu poin yang layak. Dan di antara titik -titik yang layak ada setidaknya satu, yang mengoptimalkan fungsi objektif.

Pemrograman linier dikembangkan secara mandiri oleh fisikawan dan ahli matematika Amerika.

Metode pemecahan masalah yang dikenal sebagai Metode simpleks Ini adalah penciptaan Dantzig, yang bekerja untuk Angkatan Udara AS, Universitas Berkeley dan Universitas Stanford.

Gambar 2. Matematikawan George Dantzig (kiri) dan Leonid Kantorovich (kanan). Sumber: f. Zapata.

[TOC]

Model pemrograman linier

Elemen yang diperlukan untuk membangun model pemrograman linier, sesuai dengan situasi praktis, adalah: adalah:

-Fungsi objektif

-Variabel keputusan

-Pembatasan

Dalam fungsi objektif, apa yang ingin Anda capai ditentukan. Sebagai contoh, misalkan itu diinginkan untuk memaksimalkan laba yang diperoleh dari pembuatan produk tertentu. Maka fungsi "laba" ditetapkan, sesuai dengan harga di mana produk dijual.

Dalam istilah matematika, fungsi ini dapat dinyatakan disingkat menggunakan penjumlahan:

Z = ∑k_yo X_yo

Dalam persamaan ini, k_yo Mereka koefisien dan x_yo adalah variabel keputusan.

Variabel keputusan adalah elemen sistem yang kontrolnya dan nilainya adalah bilangan real positif. Dalam contoh yang diusulkan, variabel keputusan adalah jumlah masing -masing produk yang akan diproduksi untuk mendapatkan gain maksimum.

Akhirnya, kami memiliki pembatasan, yang merupakan persamaan linier atau ketidaksetaraan dalam hal variabel keputusan. Mereka menggambarkan keterbatasan masalah, yang diketahui dan dapat misalnya jumlah bahan baku yang tersedia dalam pembuatan.

Dapat melayani Anda: fungsi lebih tinggi dari dua (contoh)

Jenis pembatasan

Anda dapat memiliki jumlah batasan M, mulai dari J = 1 sampai J = m. Secara matematis pembatasannya terdiri dari tiga jenis:

1. KE_J = ∑ a_{aku j} . X_yo
2. B_J ≥ ∑ b_{aku j} . X_yo
3. C_J ≤ ∑ c_{aku j} . X_yo

Pembatasan pertama adalah tipe persamaan linier dan berarti bahwa nilainya_J, yang diketahui, harus dihormati.

Dua pembatasan yang tersisa adalah anjuran linier dan berarti bahwa nilai B_J dan C_J, diketahui, dapat dihormati atau diatasi, ketika simbol yang muncul ≥ (lebih besar atau sama dengan) atau menghormati atau tidak diatasi, jika simbolnya ≤ (kurang dari atau sama dengan).

Contoh model

Bidang aplikasi sangat beragam, mencakup dari administrasi bisnis hingga nutrisi, tetapi untuk memahami metode ini, model sederhana dari situasi praktis dengan dua variabel kemudian diusulkan.

Pastry lokal dikenal dengan dua spesialisasi: Kue Hutan Hitam dan Kue Sacrisa.

Dalam elaborasi mereka membutuhkan telur dan gula. Untuk hutan hitam, 9 telur dan 500 g gula diperlukan, sedangkan 8 telur dan 800 g gula diperlukan untuk sacripenin. Harga penjualan masing -masing adalah $ 8 dan 10.

Masalahnya adalah: berapa banyak kue dari masing -masing jenis yang harus dibuat kue untuk memaksimalkan gainnya, mengetahui bahwa ia memiliki 10 kilo gula dan 144 telur?

Variabel keputusan

Variabel keputusan adalah "x" dan "y", yang mengambil nilai nyata:

-X: Jumlah kue hutan hitam

-Y: Kue tipe sacrifantine.

Pembatasan

Pembatasan diberikan oleh fakta bahwa jumlah kue adalah jumlah positif dan ada jumlah bahan baku yang terbatas untuk mempersiapkannya.

Oleh karena itu, dengan cara matematika, pembatasan ini memperoleh formulir:

1. x ≥ 0
2. dan ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 dan ≤ 10

Pembatasan 1 dan 2 merupakan Kondisi non -negativitas sebelumnya terpapar, dan semua anjuran yang diangkat adalah linier. Dalam pembatasan 3 dan 4 adalah nilai -nilai yang tidak boleh diatasi: 144 telur dan 10 kg gula.

Fungsi objektif

Akhirnya, fungsi objektif adalah keuntungan yang diperoleh dengan memproduksi "x" jumlah kue hutan hitam ditambah jumlah sakristin "y". Itu dibangun harga pengalikan dengan jumlah kue yang dibuat dan ditambahkan untuk setiap jenis. Ini adalah fungsi linier yang akan kita sebut g (x, y):

G = 8x + 10y

Metode solusi

Di antara berbagai metodologi solusi adalah metode grafis, algoritma simpleks dan metode titik dalam, untuk menyebutkan beberapa.

- Metode grafik atau geometris

Ketika Anda memiliki masalah dua variabel seperti bagian sebelumnya, pembatasan menentukan daerah poligonal di pesawat Xy, panggilan wilayah yang layak salah satu Wilayah viabilitas.

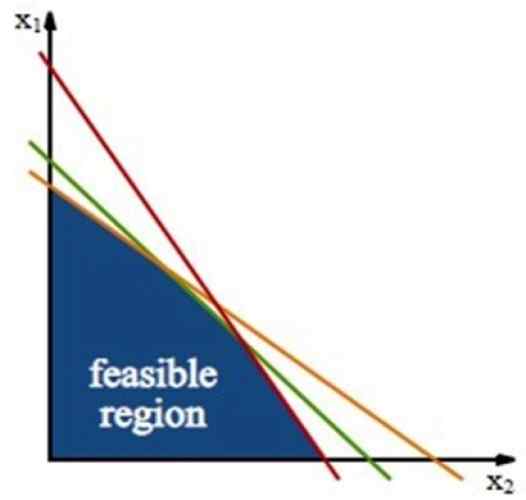Gambar 3. Wilayah yang layak, di mana solusi dari masalah optimasi berada. Sumber: Wikimedia Commons.

Wilayah ini dibangun melalui Baris pembatasan, yang merupakan garis yang diperoleh dari ketidaksetaraan pembatasan, hanya bekerja dengan tanda kesetaraan.

Dapat melayani Anda: Himpunan terbatas: properti, contoh, latihan terpecahkan

Dalam kasus toko roti yang ingin mengoptimalkan keuntungan, garis pembatasan adalah:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Semua titik di wilayah yang dikunci oleh garis -garis ini adalah solusi yang mungkin, jadi ada yang tak terbatas. Kecuali dalam kasus di mana wilayah yang layak kosong, dalam hal ini masalah yang diangkat tidak memiliki solusi.

Untungnya, untuk masalah kue, wilayah yang layak tidak kosong, kami memilikinya di bawah.

Gambar 4. Wilayah yang layak dari masalah kue. Garis lurus 0 melintasi asal. Sumber: f. Zapata dengan Geogebra.

Solusi optimal, jika ada, adalah dengan bantuan fungsi objektif. Misalnya, ketika datang untuk menemukan gain g maksimum, Anda memiliki baris berikut, yang disebut ISO-BENEFICE Lurus:

G = k₁x + k₂dan → y = -k₁x / k₂ + G/ k₂

Dengan garis ini semua pasangan (x, y) diperoleh yang memberikan gain g yang diberikan, jadi ada keluarga garis sesuai dengan nilai g, tetapi semua dengan kemiringan -k yang sama₁ / k₂, sehingga mereka sejajar lurus.

Solusi optimal

Sekarang, dapat ditunjukkan bahwa solusi optimal dari masalah linier selalu merupakan ekstrem atau simpul dari daerah yang layak. Jadi:

Solusi garis adalah yang terjauh dari asal dan yang memiliki setidaknya satu titik yang sama dengan wilayah yang layak.

Jika garis yang paling dekat dengan asal memiliki seluruh segmen yang sama dengan wilayah yang layak, dikatakan bahwa ada solusi tak terbatas. Kasing ini terjadi jika kemiringan garis ISO-manfaat sama dengan yang dari jalur lain yang membatasi wilayah tersebut.

Untuk kue kami, simpul kandidat adalah A, B dan C.

- Metode Dantzig Simplex

Metode grafik atau geometris berlaku untuk dua variabel. Namun, lebih rumit ketika ada tiga variabel, dan tidak mungkin digunakan untuk sejumlah besar variabel.

Ketika datang ke masalah lebih dari dua variabel, Metode simpleks, yang terdiri dari serangkaian algoritma untuk mengoptimalkan fungsi objektif. Matriks sederhana dan aritmatika biasanya digunakan untuk melakukan perhitungan.

Metode simpleks dimulai dengan memilih solusi yang layak dan memeriksa apakah optimal. Jika kita sudah memecahkan masalah, tetapi jika tidak, itu terus menuju solusi yang lebih dekat dengan optimasi. Jika solusinya ada, algoritma dengan itu dalam beberapa upaya.

Dapat melayani Anda: apa rentang statistiknya? (Dengan contoh)

Aplikasi

Pemrograman linier dan non-linear yang diterapkan di banyak bidang untuk membuat keputusan terbaik dalam mengurangi biaya dan meningkatkan laba, yang tidak selalu moneter, karena mereka dapat diukur dalam waktu, misalnya, jika Anda berusaha meminimalkan waktu yang diperlukan untuk melakukan yang diperlukan untuk melaksanakan serangkaian operasi.

Berikut adalah beberapa bidang:

-Dalam pemasaran digunakan untuk menemukan kombinasi media terbaik (jejaring sosial, televisi, pers dan lainnya) untuk mengiklankan produk tertentu.

-Untuk alokasi pekerjaan yang sesuai dengan personel perusahaan atau pabrik atau jadwal kepada mereka.

-Dalam pemilihan makanan yang paling bergizi dan dengan biaya terendah di industri ternak dan unggas.

Latihan terpecahkan

- Latihan 1

Grafik Model pemrograman linier yang diangkat di bagian sebelumnya.

Larutan

Perlu untuk grafik set nilai yang ditentukan oleh sistem pembatasan yang ditentukan dalam masalah:

1. x ≥ 0
2. dan ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 dan ≤ 10

Wilayah yang diberikan oleh Inquations 1 dan 2 sesuai dengan kuadran pertama bidang Cartesian. Sedangkan untuk ketidaksetujuan 3 dan 4, itu dimulai dengan menemukan garis pembatasan:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

Wilayah yang layak adalah segi empat yang simpulnya adalah titik A, B, C dan D.

Gain minimum adalah 0, oleh karena itu garis 8x + 10 dan 10 adalah batas bawah dan garis ISO -BENEFIT memiliki tertunda -8/10 = -0.8.

Nilai ini berbeda dari lereng garis pembatasan lainnya dan karena wilayah yang layak terbatas, ada solusi unik.

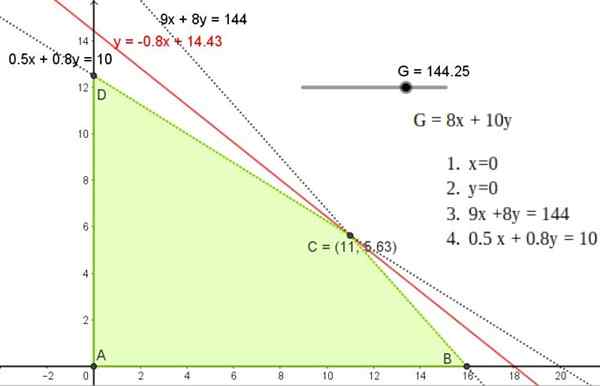Gambar 5. Solusi grafis Latihan 1, menunjukkan wilayah yang layak dan solusi titik C di salah satu simpul wilayah tersebut. Sumber: f. Zapata.

Solusi ini sesuai dengan garis kemiringan -0.8 yang melewati salah satu poin A, B atau C, yang koordinatnya adalah:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Solusi optimal

Kami menghitung nilai g untuk masing -masing poin ini:

-(11; 5.625): g_KE = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): g_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

Keuntungan terbesar adalah memproduksi 11 kue hutan hitam dan 5.625 Kue Sacripantine. Solusi ini setuju dengan yang ditemukan melalui perangkat lunak.

- Latihan 2

Verifikasi hasil latihan sebelumnya dengan menggunakan fungsi Solver (Solutioner) yang tersedia di sebagian besar spreadsheet seperti Excel atau Calc de Libreoffice, yang menggabungkan algoritma Simplex untuk optimasi pemrograman linier.

Larutan

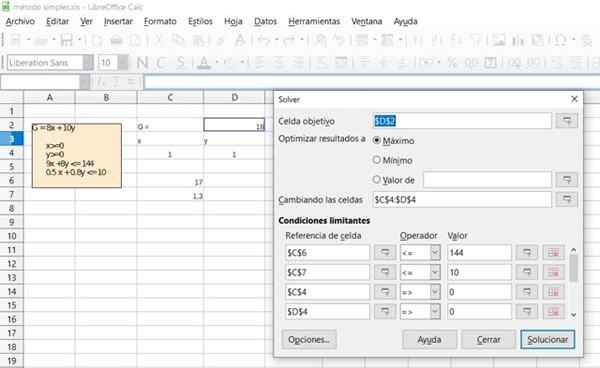Gambar 6. Detail Solusi Latihan 1 Melalui Spreadsheet Kantor Kantor Gratis. Sumber: f. Zapata. 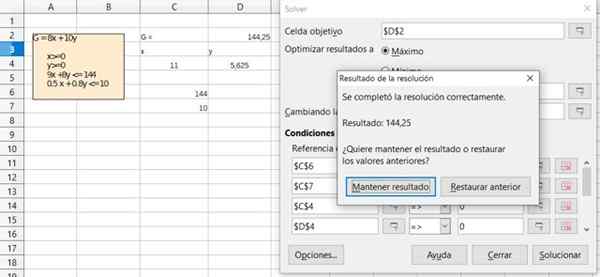Gambar 7. Detail Solusi Latihan 1 Melalui Spreadsheet Kantor Kantor Gratis. Sumber: f. Zapata.

Referensi

1. Cemerlang. Pemrograman linier. Pulih dari: brilian.org.
2. Eppen, g. 2000. Penelitian Operasi dalam Ilmu Administrasi. Ke -5. Edisi. Prentice Hall.
3. Haeussler, e. 1992. Matematika untuk Administrasi dan Ekonomi. 2nd. Edisi. Ibero -American Editorial Group.
4. Hiru.Eus. Pemrograman linier. Pulih dari: hiru.Eus.
5. Wikipedia. Pemrograman linier. Pulih dari: is. Wikipedia.org.