Jum Properti Asosiatif, Perkalian, Contoh, Latihan

Itu properti asosiatif dari jumlah tersebut mewakili sifat asosiatif dari operasi yang ditambahkan dalam berbagai set matematika. Ini menceritakan tiga (atau lebih) elemen dari set ini, disebut a, b dan c, sehingga selalu terpenuhi:

a + (b + c) = (a + b) + c

Dengan cara ini dijamin bahwa, terlepas dari bagaimana mengelompokkan untuk melakukan operasi, hasilnya sama.

Gambar 1. Kami menggunakan properti asosiatif dari jumlah berkali -kali saat melakukan operasi aritmatika dan aljabar. (Menggambar: Komposisi Freepik: F. Zapata)

Tetapi harus dicatat bahwa properti asosiatif tidak identik dengan properti komutatif. Artinya, kita tahu bahwa urutan addends tidak mengubah jumlah atau bahwa urutan faktor tidak mengubah produk. Jadi untuk jumlah yang dapat Anda tulis seperti ini: A + B = B + A.

Namun, di properti asosiatif berbeda, karena urutan elemen yang akan ditambahkan dipertahankan dan apa perubahan operasi yang dieksekusi terlebih dahulu. Yang berarti tidak masalah terlebih dahulu (b+c) dan untuk hasil ini tambahkan ke, untuk mulai menambahkan ke b dan ke hasil tambahkan c.

Banyak operasi penting seperti jumlahnya asosiatif, tetapi tidak semua. Misalnya dalam pengurangan bilangan real itu terjadi bahwa:

A - (b - c) ≠ (a - b) - c

Ya A = 2, b = 3, c = 1, lalu:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Properti asosiatif dari perkalian

Seperti yang dilakukan untuk jumlah, properti asosiatif dari perkalian menunjukkan bahwa:

A ˟ (B ˟ C) = (A ˟ B) ˟ C

Dapat melayani Anda: jumlah polinomial, seperti yang dilakukan, contoh, latihan

Dalam hal set bilangan real, mudah untuk memverifikasi bahwa itu selalu. Misalnya, menggunakan nilai a = 2, b = 3, c = 1, Anda harus:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Angka -bilangan real memenuhi properti asosiatif dari jumlah dan perkalian. Di sisi lain, di set lain, seperti vektor, jumlahnya asosiatif, tetapi produk silang atau produk vektor tidak.

Aplikasi properti asosiatif perkalian

Keuntungan bahwa operasi di mana properti asosiatif terpenuhi adalah pengelompokan dengan cara yang paling nyaman dipenuhi. Ini sangat memfasilitasi resolusi.

Misalnya, misalkan di perpustakaan kecil ada 3 rak dengan masing -masing 5 hiburan. Di setiap hiburan ada 8 buku. Berapa banyak buku yang total?

Kami dapat melakukan operasi sebagai berikut: Total Buku = (3 x 5) x 8 = 15 x 8 = 120 Buku.

Atau lebih: 3 x (5 x 8) = 3 x 40 = 120 buku.

Gambar 2. Aplikasi properti asosiatif dari perkalian adalah untuk menghitung jumlah buku di setiap rak. Gambar yang dibuat oleh f. Zapata.

Contoh

-Dalam set bilangan alami, utuh, rasional, nyata dan kompleks, properti asosiatif dari jumlah dan perkalian terpenuhi.

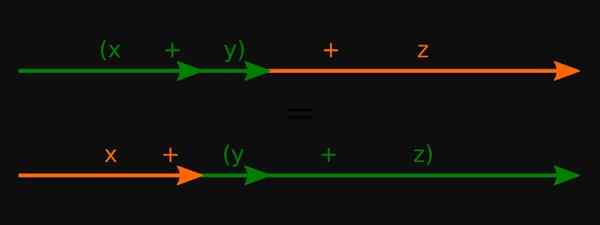Gambar 3. Untuk bilangan real, properti asosiatif dari jumlah itu terpenuhi. Sumber: Wikimedia Commons.

-Untuk polinomial mereka juga berlaku dalam operasi ini.

-Dalam kasus operasi pengurangan, pembagian dan eksponensial, properti asosiatif tidak dipenuhi dalam bilangan real atau polinomial.

Dapat melayani Anda: orthoedro: rumus, area, volume, diagonal, contoh

-Dalam kasus matriks, properti asosiatif dipenuhi untuk jumlah dan perkalian, meskipun dalam kasus terakhir, komutasi tidak terpenuhi. Ini berarti bahwa, matriks yang diberikan A, B dan C, memang benar bahwa:

(A x b) x c = a x (b x c)

Tapi ... a x b ≠ b x a

Properti asosiatif di vektor

Vektor membentuk set yang berbeda dari bilangan real atau bilangan kompleks. Operasi yang ditentukan untuk set vektor agak berbeda: ada jumlah, pengurangan dan tiga jenis produk.

Jumlah vektor memenuhi properti asosiatif, serta angka, polinomial dan matriks. Adapun produk skalar, memanjat dengan vektor dan salib yang dibuat antara vektor, yang terakhir tidak memenuhi, tetapi produk skalar, yang merupakan jenis operasi lain antara vektor, memang memuaskannya, dengan mempertimbangkan hal berikut:

-Produk skalar untuk vektor menghasilkan vektor.

-Dan dengan mendaki dua vektor, itu adalah skalar.

Oleh karena itu, diberi vektor v, atau Dan W, Dan juga skalar λ, dimungkinkan untuk menulis:

-Jumlah vektor: v +(atau + W ) = (v + atau) + W

-Produk skalar: λ (v • atau ) = (λv) • atau

Yang terakhir ini dimungkinkan berkat apa v • atau Itu adalah skalar, dan λv Itu adalah vektor.

Namun:

v × (atau × W ) ≠ (v × atau)×W

Faktorisasi polinomial dengan memicu istilah pengelompokan

Aplikasi ini sangat menarik, karena seperti yang dinyatakan di atas, properti asosiatif membantu menyelesaikan masalah tertentu. Jumlah monomial adalah asosiatif dan ini dapat digunakan untuk faktor ketika faktor umum yang jelas tidak muncul pada pandangan pertama.

Dapat melayani Anda: Cembung Poligon: Definisi, Elemen, Properti, Contoh

Misalnya, misalkan itu diminta untuk memperhitungkan: X³ + 2X² + 3X +6. Polinomial ini tidak memiliki faktor umum, tetapi mari kita lihat apa yang terjadi jika dikelompokkan dengan cara ini:

X³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Tanda kurung pertama sebagai faktor umum X²:

X³ + 2X² = X² (x+2)

Di kedua faktor umum adalah 3:

3x +6 = 3 (x + 2)

Jadi:

X³ + 2X² + 3X +6 = X²(x+ 2)+ 3 (x+ 2)

Sekarang ada faktor umum yang jelas, yaitu x+2:

X²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Latihan

- Latihan 1

Bangunan sekolah memiliki 4 lantai dan di masing -masing ada 12 ruang kelas dengan 30 meja di dalamnya. Berapa banyak meja yang dimiliki sekolah secara total?

Larutan

Masalah ini diselesaikan dengan menerapkan properti asosiatif perkalian, mari kita lihat:

Jumlah Total Meja = 4 Lantai X 12 Kelas /Lantai X 30 Meja /Kelas = (4 x 12) x 30 meja = 48 x 30 = 1440 meja.

O Jika lebih disukai: 4 x (12 x 30) = 4 x 360 = 1440 meja

- Latihan 2

Diberikan polinomial:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Terapkan properti asosiatif dari jumlah untuk menemukan (x) + b (x) + c (x).

Larutan

Dua yang pertama dapat dikelompokkan dan hasilnya menambahkan yang ketiga:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Polinomial C (x) segera ditambahkan:

[X⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Pembaca dapat memverifikasi bahwa hasilnya identik jika diselesaikan dengan opsi a (x) + [b (x) + c (x)]].

Referensi

1. Jiménez, r. 2008. Aljabar. Prentice Hall.
2. Matematika itu menyenangkan. Hukum komutatif, asosiatif dan distrik. Pulih dari: Mathisfun.com.
3. Gudang Matematika. Definisi properti asosiatif. Dipulihkan dari: Mathwarehouse.com.
4. Ilmu pengetahuan. Properti asosiatif & komutatif dari penambahan & perkalian (dengan contoh). Pulih dari: ilmuwan.com.
5. Wikipedia. Properti asosiatif. Diperoleh dari: di.Wikipedia.org.