Matematika

Sifat radikal

959
258
Jessie Harvey

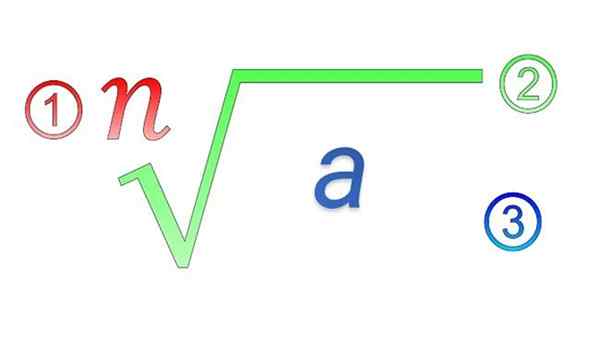
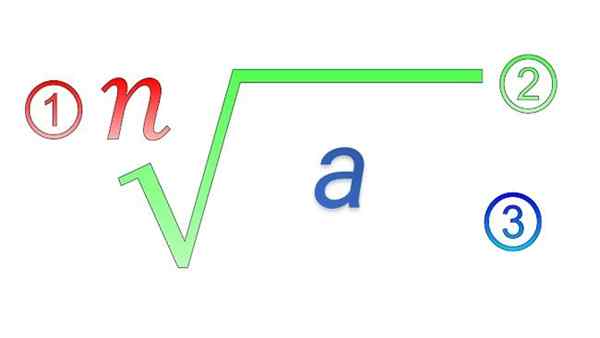Elemen Radikal: 1) Indeks; 2) simbol radikal; 3) Kuantitas subradical

Apa sifat radikal?

Itu sifat radikal Mereka adalah operasi yang memungkinkan penyelesaian masalah radikal dan kekuatan yang kompleks. Radikal adalah cara untuk melambangkan secara matematis ke n-eme dari jumlah "a". Akar ini adalah jumlah lain, yang disebut "B", sehingga namanya tepat "A", jadi valid untuk menulis yang berikut:

$\dpi110 \sqrt[n]a=b\Rightarrow b^n=a$

Nilai "n" adalah angka alami, yang dikenal sebagai indeks root, "a" adalah Raih atau kuantitas subradical, dan "b" adalah n-eme dari "root". Baik "A" dan "B" milik set bilangan real.

Jika indeks tidak ditulis dalam radikal, segera dipahami bahwa nilainya sama dengan 2 dan bertuliskan "akar kuadrat a".

Karena "n" milik set bilangan alami, itu bisa menjadi pasangan atau angka ganjil. Kemudian, kasus -kasus berikut dibedakan:

Untuk "n" par

Jika a> 0 atau sama dengan 0, akar N-alkal "A" adalah positif atau 0, dan dipanggil akar utama.
Kapan harus < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Untuk "n" aneh

Ya A> 0, N-EME dari root "A" adalah positif.
Kapan harus< 0, la raíz n-ésima de “a” es negativa.

Beberapa contoh adalah sebagai berikut:

$\dpi110 \sqrt49=7\Rightarrow 7^2=49$

$\dpi110 \sqrt[3]\left ( -729 \right )=-9\Rightarrow \left ( -9 \right )^3=-729$

$\dpi110 \sqrt3=1.7320508…$

Properti Pembuatan Film

Dimungkinkan untuk menulis nama sejumlah jumlah sebagai kekuatan dengan eksponen fraksional, yaitu, bilangan rasional.

Dalam hal ini, indeks root menjadi penyebut, sedangkan eksponen jumlah subradical menjadi pembilang:

Dapat melayani Anda: fungsi homografi: cara grafik, latihan terpecahkan

$\dpi110 \sqrt[n]a^m=a^\fracmn$

Ekspresi yang valid selama n ≠ 0, karena tidak ada pecahan dengan penyebut yang diterima.

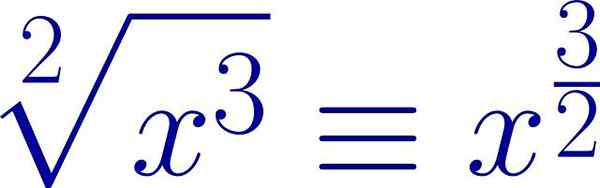Contoh ekspresi radikal yang ditulis dalam bentuk eksponen fraksional. Indeks root adalah penyebut eksponen, sedangkan kekuatan siaran adalah pembilang. Sumber: Wikimedia Commons.

Dengan cara ini, sifat yang sama yang berlaku untuk kekuatan, dapat digunakan dalam kasus radikal.

Untuk nilai -nilai milik set bilangan real, properti ini adalah sebagai berikut:

1. Produk radikal dari indeks yang sama

Dalam produk dari dua (atau lebih) radikal dari indeks yang sama, jumlah subradical dikalikan, mempertahankan indeks:

$\dpi110 \sqrt[n]a\cdot \sqrt[n]b=\sqrt[n]a\cdot b$

2. Hasil bagi radikal dari indeks yang sama

Hasil bagi antara akar N-itu dari "A" dan N-EME-EMI "B", menjadi B ≠ 0, sama dengan akar n-emeasy dari hasil bagi antara "A" dan "B":

$\dpi110 \frac\sqrt[n]a\sqrt[n]b=\sqrt[n]\fracab$

3. Root root

Untuk menemukan akar n-emeasy dari M-EME dari jumlah "A", jumlah subradical ditulis di bawah root yang indeksnya adalah produk antara "n" dan "m":

$\dpi110 \sqrt[n]\sqrt[m]a=\sqrt[n\cdot m]a$

Prosedur ini mudah diperluas ke akar bersarang berturut -turut. Indeks root yang dihasilkan adalah produk dari semua indeks, seperti ini:

$\dpi110 \sqrt[n]\sqrt[m]\sqrt[p]\sqrt[q]a=\sqrt[n\cdot m\cdot p\cdot q]a$

4. Daya root

N-bahwa, dinaikkan ke kekuatan M, mengekspresikan jumlah subradical untuk kekuatan tersebut:

$\dpi110 \left ( \sqrt[n]a \right )^m=\sqrt[n]a^m=a^\fracmn$

Kasus -kasus tertentu:

1) Ya n = m, Tanda akar menghilang, meninggalkan pangkalan yang ditinggikan ke daya 1:

$\dpi110 \left ( \sqrt[n]a \right )^n=\sqrt[n]a^n=a$

Yang berlaku untuk ≥ 0. Secara umum, jika indeks root adalah angka genap, Anda memiliki:

$\dpi110 \left ( \sqrt[n]a \right )^n=\left| a\right|$

(Lihat contoh nanti)

2) Ya m> n, Fraksi M/N tidak tepat dan root dapat disederhanakan, misalnya, mencari fraksi yang setara dengan M/N sedemikian rupa sehingga pembilang dan penyebut adalah sepupu satu sama lain, atau menulis ulang jumlah subradikal dan menerapkan beberapa dari Properti yang dijelaskan di sini.

Dapat melayani Anda: prisma dan piramida

(Lihat contoh nanti)

5. Amplifikasi radikal

Radikal dapat diperkuat dengan faktor Q, Jika kedua indeks root, serta kekuatan kuantitas subradikal, berlipat ganda dengan faktor tersebut, dan operasi ini tidak memerlukan modifikasi hasil. Karena itu:

$\dpi110 \sqrt[n]a^m=\sqrt[n\cdot q]a^m\cdot q$

Asalkan A ≥ 0 saat itu bahkan.

6. Pengenalan faktor dalam radikal

Jika faktor "B" positif mengalikan radikal, ia dapat melewati di dalamnya, jika naik ke indeks root yang sama. Dalam hal itu:

$\dpi110 b\sqrt[n]a^m=\sqrt[n]b^n\cdot a^m$

7. Jumlah dan pengurangan radikal

Radikal dapat menambah dan mengurangi, selama mereka adalah indeks yang sama dan memiliki jumlah subradikal yang sama.

Ketika dua atau lebih radikal memiliki jumlah indeks dan subradical yang sama, dikatakan bahwa mereka Radikal serupa.

Misalnya, radikal berikut ini serupa:

$\dpi110 \sqrt[3]5,\: -7\sqrt[3]5,\: 10\sqrt[3]5$

Sebaliknya, radikal ini tidak serupa, karena mereka tidak memiliki jumlah subradical yang sama:

$\dpi110 \sqrt2,\: \sqrt3$

Dua ini juga tidak serupa:

$\dpi110 \sqrt7,\: \sqrt[4]7$

Karena indeks radikal tidak sama.

Radikal serupa dapat dikurangi menjadi satu, menambah atau mengurangi koefisien yang menyertainya.

Contoh sifat radikal

Contoh 1

Berapa nilai dari akar berikut?

$\dpi110 \sqrt32,\: \sqrt[3]-8,\: \sqrt[4]81,\: \sqrt-8$

Akar kuadrat 32 dapat ditemukan langsung dengan bantuan kalkulator. Nilainya adalah:

$\dpi110 \sqrt32=5.656854249…$

Poin -poin suspensi menunjukkan bahwa ada desimal yang tak terbatas.

Jika Anda lebih suka tidak bekerja dengan bilangan desimal, akar kuadrat dari 32 juga dapat dihitung dengan mendekomposisi 32 dalam faktor utamanya:

32 = 2⁵

Dengan cara ini, saat mengganti, itu diperoleh:

Dapat melayani Anda: pembagi 8: apa itu dan penjelasan yang mudah

$\dpi110 \sqrt32=\sqrt2^5$

Ditulis sebagai eksponen fraksional:

$\dpi110 \sqrt32=\sqrt2^5=2^\frac52$

Fraction 5/2 tidak tepat, sehingga radikal dapat disederhanakan, menggunakan sifat -sifat kekuatan:

$\dpi110 \sqrt32=\sqrt2^5=\sqrt2\cdot 2^4$

Sekarang menerapkan properti 1 di atas:

$\dpi110 \sqrt2\cdot 2^4=\sqrt2\cdot \sqrt2^4=\sqrt2\cdot \sqrt16=4\sqrt2$

Karena itu:

$\dpi110 \sqrt32=4\sqrt2$

Untuk bagian ini:

$\dpi110 \sqrt[3]-8=-2$

Sejak (−2)³ = −8.

Menurut Properti 4:

$\dpi110 \sqrt[4]81=\sqrt[4]3^4=3$

Dan akhirnya, akar kuadrat −8 tidak ada dalam set bilangan real, meskipun dalam bilangan kompleks.

Contoh 2

Mengingat operasi berikut:

$\dpi110 4\sqrt8+\sqrt81-3\sqrt32$

Apakah mungkin untuk mengurangi hasilnya?

Dengan ketentuan bahwa radikal serupa, dimungkinkan untuk menguranginya, tetapi untuk ini mereka harus memiliki indeks yang sama dan kuantitas subradical yang sama. Dalam contoh sebelumnya terlihat bahwa:

$\dpi110 \sqrt32=4\sqrt2$

Prosedur analog dapat digunakan untuk menulis penambahan pertama, sehingga jumlah subradical sama dengan 2:

$\dpi110 4\sqrt8=4\sqrt2^3=4\sqrt2^2\cdot 2=4\sqrt2^2\cdot \sqrt2=4\cdot 2\cdot\sqrt2=8\sqrt2$

Radikal ini mirip dengan sebelumnya. Adapun akar kuadrat 81, ini adalah 9, oleh karena itu: oleh karena itu:

$\dpi110 4\sqrt8+\sqrt81-3\sqrt32=8\sqrt2+9-3\cdot 4\sqrt2=8\sqrt2+9-12\sqrt2=(8-12)\sqrt2+9=-4\sqrt2+9$

Contoh 3

Properti apa yang diperlukan untuk diterapkan untuk melakukan operasi ini?

$\dpi110 \sqrt[3]x\sqrtx$

Kita harus menerapkan properti 3 dan 5, yang, masing -masing, akar dari root dan pengenalan nilai radikal. Pertama, properti 5 berlaku, untuk memperkenalkan "x" yang berada di luar akar terdalam:

$\dpi110 \sqrt[3]x\sqrtx=\sqrt[3]\sqrtx^2\cdot x=\sqrt[3]\sqrtx^3$

Dan sekarang ekspresi siap untuk menerapkan properti 3, dan gandakan masing -masing indeks dari masing -masing radikal:

$\dpi110 \sqrt[3]x\sqrtx=\sqrt[3]\sqrtx^2\cdot x=\sqrt[3]\sqrtx^3=\sqrt[6]x^3$

Referensi

Gonzales, d. 2011. Aljabar Dasar: Teori dan Praktek. 2nd. Edisi.
Haeussler, e. 2012. Prekalkulasi. 1st. Edisi. Pearson.
Khan Acadaem. Eksponen dan radikal. Pulih dari: Khanacademy.org.
Larson, r. 2012. Prekalkulasi. Ke -8. Edisi. Pembelajaran Cengage.
Stewart, J. 2007. Matematika untuk perhitungan. Ke -5. Edisi. Pembelajaran Cengage.