Apa momen magnetis?

Dia Momen magnetik Ini adalah vektor yang menghubungkan arus yang melintasi sedikit atau loop tertutup dengan luas yang sama. Modulnya sama dengan produk intensitas arus oleh area, dan arah dan arahnya diberikan oleh aturan kanan, seperti yang ditunjukkan pada Gambar 1.

Definisi ini valid. Adapun kesatuan momen magnetik, dalam sistem unit internasional jika itu ampere × m².

Gambar 1. Vektor momen magnetik dari ikatan arus arbitrer tegak lurus terhadap bidangnya dan arah ditentukan oleh aturan ibu jari kanan. Sumber: Wikimedia Commons.

Dalam istilah matematika, menunjukkan momen magnetik vektor dengan lirik Yunani μ (Dalam tebal karena itu adalah vektor dan dengan demikian membedakan dirinya dari besarnya), ia dinyatakan sebagai:

μ = Ia N

Di mana saya adalah intensitas arus, a adalah area yang menutupi loop dan N Ini adalah vektor unit (modul sama dengan 1) yang menunjuk ke arah tegak lurus terhadap bidang spase, dan yang maknanya diberikan oleh aturan ibu jari kanan (lihat Gambar 1).

Aturan ini sangat sederhana: melengkung keempat jari tangan kanan sehingga mereka mengikuti arus, ibu jari menunjukkan arah dan arah N dan karena itu momen magnetis.

Persamaan sebelumnya berlaku untuk loop. Jika ada nougas seperti dalam kumparan, momen magnetik dikalikan dengan n:

μ = nIa N

[TOC]

Momen magnet dan medan magnet

Sangat mudah untuk menemukan ekspresi untuk momen magnetik belokan dengan bentuk geometris biasa:

-Sisi persegi sisi ℓ: μ = Iℓ² N

-Sisi spiral persegi panjang ke Dan B: μ = Iab N

-Radio R. Radio Spira: μ = Iπr² N

Dapat melayani Anda: nomor atom

Medan Magnet Dipolo

Medan magnet yang dihasilkan oleh loop atau spase saat ini menyerupai magnet bar dan juga dari bumi.

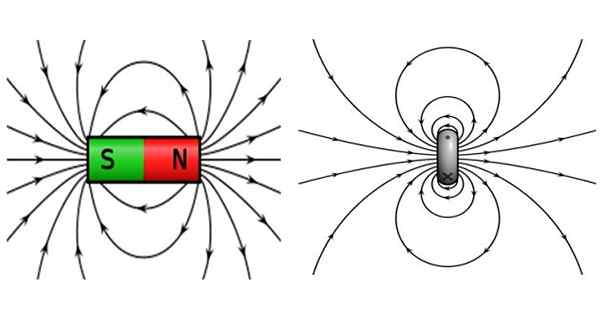Gambar 2. Di sebelah kiri medan magnet magnet batang dan ke kanan yang menghasilkan spiral melingkar yang mengangkut arus. Sumber: Wikimedia Commons.

Magnet batang ditandai dengan memiliki kutub utara dan kutub selatan, di mana kutub yang berlawanan tertarik dan kutub yang sama mengusir. Garis lapangan ditutup, tinggalkan Kutub Utara dan mencapai Kutub Selatan.

Sekarang, tiang magnet tidak dapat dipisahkan, yang berarti bahwa jika magnet bar dibagi menjadi dua magnet yang lebih kecil, mereka terus memiliki kutub utara dan selatan mereka sendiri. Tidak mungkin untuk memiliki tiang magnetik yang terisolasi, itulah sebabnya magnet bar disebut Dipolo magnetik.

Medan magnet dari jari-jari r spiral, yang mengangkut I saat ini, dihitung oleh hukum biot-savart. Untuk titik -titik milik sumbu simetri (dalam hal ini sumbu x), bidang diberikan oleh:

Dimana μ_{salah satu} Ini adalah permeabilitas vakum. Mengambil lapangan pada titik -titik jauh dari spase, yang dipenuhi x >> r, lapangan mendekati:

Hubungan antara medan magnet dan momen magnetik dipolo

Termasuk momen magnetik dalam ekspresi sebelumnya adalah:

Dengan cara ini, intensitas medan magnet sebanding dengan momen magnetik. Perhatikan bahwa intensitas bidang berkurang dengan kubus jarak.

Pendekatan ini berlaku untuk loop apa pun, selama X menjadi besar dibandingkan dengan dimensinya.

Dan karena garis -garis bidang ini menyerupai magnet bar, persamaan adalah model yang baik untuk medan magnet ini dan sistem lain yang garisnya serupa, seperti: misalnya:

Dapat melayani Anda: absorbansi: apa itu, contoh dan latihan diselesaikan

-Partikel dimuat dalam gerak sebagai elektron.

-Atom.

-Bumi dan planet lain dan satelit tata surya.

-Bintang.

Efek bidang eksternal pada loop

Karakteristik yang sangat penting dari momen magnetik adalah hubungannya dengan torsi yang dialami loop di hadapan medan magnet eksternal.

Motor listrik berisi kumparan yang melaluinya aliran arah yang berubah dan berkat bidang eksternal mengalami efek giliran. Giliran ini membuat gerakan sumbu dan energi listrik menjadi energi mekanik selama proses.

Torsi pada loop persegi panjang

Misalkan, untuk memfasilitasi perhitungan, sisi persegi panjang ke Dan B, yang vektor normal N, Layar keluar, awalnya tegak lurus terhadap medan magnet yang seragam B, Seperti pada Gambar 3. Sisi -sisi kekuatan pengalaman loop yang diberikan oleh:

F = IL X B

Di mana L Ini adalah vektor besarnya sama dengan panjang segmen dan diarahkan sesuai dengan arus, dan merupakan intensitas yang sama dan B Itu adalah bidangnya. Gaya tegak lurus terhadap keduanya L Seperti lapangan, tetapi tidak semua sisi mengalami kekuatan.

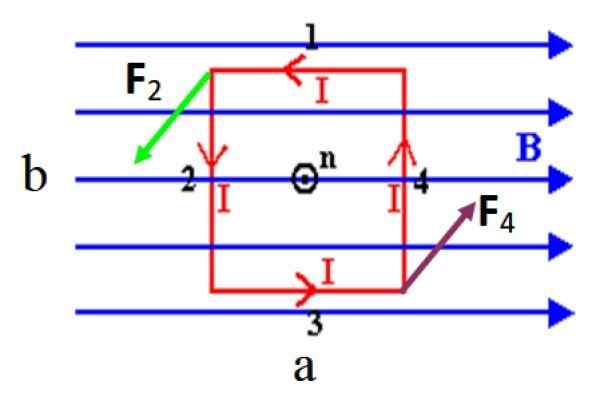Gambar 3. Spiral persegi panjang yang mengangkut I saat ini dalam arti anti -ulet, mengalami torsi di hadapan medan magnet yang seragam yang seragam. Sumber: f. Zapata.

Pada gambar yang ditunjukkan, tidak ada kekuatan pada sisi pendek 1 dan 3 karena sejajar dengan lapangan, ingat bahwa produk silang antara vektor paralel tidak berlaku. Namun, sisi panjang 2 dan 4, yang tegak lurus B, Mereka mengalami kekuatan yang digambakan sebagai F₂ Dan F₄.

Kekuatan -kekuatan ini terbentuk sepasang: Mereka memiliki besarnya dan arah yang sama, tetapi indera yang berlawanan, oleh karena itu mereka tidak dapat bergerak ke loop di tengah lapangan. Tapi mereka bisa membuatnya berputar, karena torsi  τ Bahwa masing -masing gaya memberikan, sehubungan dengan sumbu vertikal yang melewati pusat loop, ia memiliki arah dan makna yang sama.

Dapat melayani Anda: kekuatan kohesi

Menurut definisi torsi, di mana R Itu adalah vektor posisi:

τ = R X F

Jadi:

τ₂ = τ₄=(A/2) f (+J )

Torsi individu tidak dibatalkan, karena mereka memiliki arah dan makna yang sama, maka mereka ditambahkan:

τ_bersih = τ₂ + τ₄ = a f (+J )

Dan menjadi besarnya gaya F = IBB, hasilnya:

τ_bersih = I⋅a⋅b⋅b (+J )

Produk A⋅b adalah luas a dari spase, jadi IAB adalah besarnya momen magnetik μ. Karena itu τ_bersih = μ⋅b (+J )

Dapat dilihat bahwa, secara umum, torsi bertepatan dengan produk vektor antara vektor μ Dan B:

τ_bersih = μ X B

Dan meskipun ekspresi ini berasal dari loop persegi panjang, itu berlaku untuk pijakan datar secara sewenang -wenang.

Efek bidang pada loop adalah torsi yang cenderung menyelaraskan momen magnetik dengan medan.

Energi potensial dari dipol magnetik

Untuk mengubah spiral atau dipol di tengah lapangan, sebuah karya harus dilakukan terhadap gaya magnet, yang mengubah energi potensial dipolo. Variasi energi ΔU, ketika spiral berputar dari sudut θ_{salah satu} Pada sudut θ diberikan oleh integral:

Jika level referensi dipilih sebagai θ_{salah satu} = π/2:

ΔU = -μB cos θ

Yang pada gilirannya dapat dinyatakan sebagai produk skalar antara vektor B Dan μ:

ΔU = - μ ·B

Energi potensial minimum di dipol terjadi ketika cos θ = 1, yang berarti itu μ Dan B Mereka paralel, energinya maksimum jika berlawanan (θ = π) dan nol ketika mereka tegak lurus (θ = π/2).

Referensi

1. Figueroa, d. 2005. Seri: Fisika untuk Sains dan Teknik. Volume 5. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
2. Resnick, r. 1999. Fisik. Vol. 2. Edisi ke -3. di Spanyol. Perusahaan Editorial Kontinental S.KE. dari c.V.
3. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 2. Pearson.
4. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 2. 7. Ed. Pembelajaran Cengage.
5. Tipler, hlm. (2006) Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 2. Editorial dikembalikan.