Apa hubungan antara belah ketupat dan area persegi panjang?

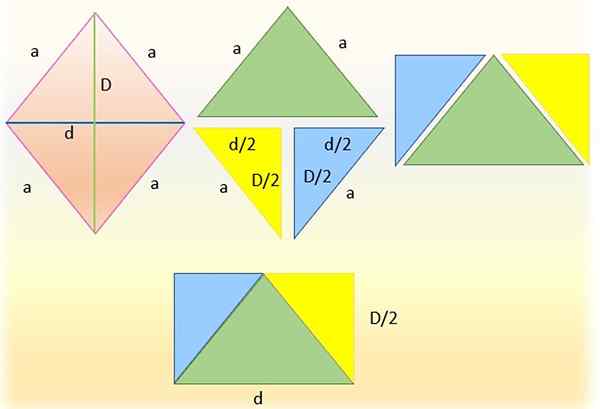
Membusuk belah ketupat untuk mendapatkan persegi panjang. Sumber: f. Zapata

Dimungkinkan untuk menghitung area belah ketupat (dan beberapa angka geometris lainnya) dari luas segitiga atau segi empat terkait, seperti jajaran genjang atau persegi panjang.

Area persegi panjang dan jajaran genjang adalah sama: dihitung sebagai produk antara pangkal gambar dan tingginya sehubungan dengan basis itu. Untuk bagiannya, area segitiga adalah produk semi -produk antara pangkalan dan tingginya.

Rumus -formula ini mudah diingat meskipun, secara alami, geometri menawarkan formula eksklusif untuk area belah ketupat, mengetahui ukuran diagonal utama dan kecil, yang dilambangkan sebagai D dan D, masing -masing:

Dimungkinkan untuk menyimpulkan ekspresi ini melalui urutan yang ditunjukkan pada gambar di atas.

Untuk melakukan ini, belah ketupat di sebelah kiri dipotong oleh salah satu diagonalnya, yang dibuat pada gambar yang dipotong oleh diagonal minor, sehingga mendapatkan dua segitiga. Segitiga atas (berwarna hijau) dibiarkan dan yang lebih rendah dibagi pada gilirannya menjadi dua segitiga, memotong setengah dari diagonal utama, mendapatkan segitiga persegi panjang identik biru dan kuning.

Kemudian hipotenus segitiga ini bertepatan dengan sisi segitiga hijau, karena mereka mengukur hal yang sama, yaitu "A". Dan persegi panjang akhirnya diperoleh, yang alasnya adalah diagonal "D" yang lebih rendah dan tingginya setengah dari diagonal utama, yaitu: "D/2".

Area persegi panjang dengan demikian membentuk bertepatan persis seperti belah ketupat, oleh karena itu dapat ditegaskan bahwa:

Dapat melayani Anda: trinomial

KE _berlian = (basis × tinggi) _{persegi panjang} = D × (d/2)

Hasil bahwa, seperti yang dapat dilihat, bertepatan dengan formula area belah ketupat yang diberikan sebelumnya.

Area Rombo dan Guardelogram

Area belah ketupat juga terkait dengan jajaran genjang, karena kedua figur geometris datar dan termasuk dalam keluarga segi empat. Misalnya, pada gambar berikut ada belah ketupat di sebelah kiri dan jajaran genjang di sebelah kanan.

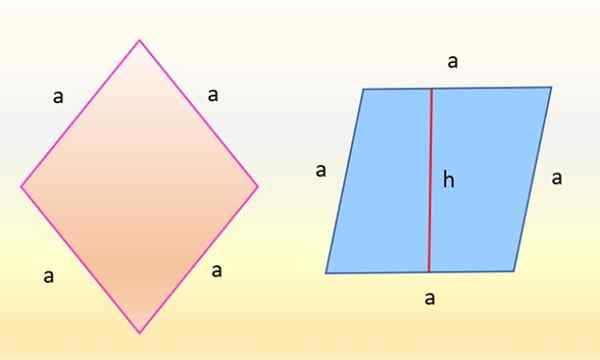Area belah ketupat di sebelah kiri sama dengan jajaran genjang di sebelah kanan. Sumber: f. Zapata

Ternyata angkanya identik, karena apa yang telah berubah hanyalah orientasi. Belah ketupat di sebelah kiri, berwarna merah muda, yang sisi -sisinya memiliki ukuran yang sama: a, diputar sedemikian rupa sehingga salah satu sisinya benar -benar horizontal. Kemudian, belah ketupat mengambil bentuk jajaran genjang biru di sebelah kanan.

Dan area jajaran genjang ini juga merupakan produk antara pangkalan "A" dan tinggi sehubungan dengan pangkalan itu, yang disebut "h" dalam gambar, oleh karena itu: oleh karena itu: oleh karena itu:

KE _genjang = A × H

Karena itu adalah angka yang sama, area ini identik dan mengikuti itu:

KE _berlian = A × H

Dengan demikian, mengetahui dan h dari jajaran genjang, luasnya dihitung dan akan bertepatan dengan belah ketupat.

Area Rombo tertulis dalam persegi panjang

Hubungan lain antara belah ketupat dan persegi panjang muncul ketika yang pertama terdaftar di dalam yang kedua. Jika ini terjadi, simpul belah ketupat bertepatan dengan titik tengah sisi persegi panjang, yang ditampilkan di bawah ini:

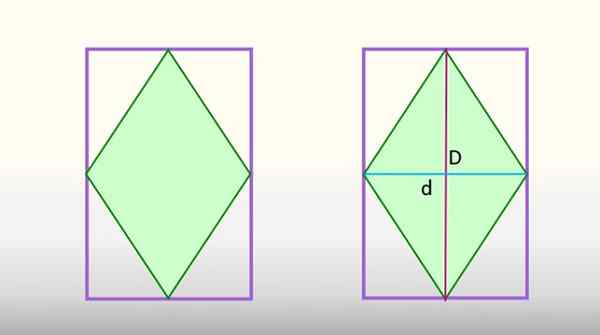Area belah ketupat tertulis dalam persegi panjang setara dengan setengah dari area persegi panjang. Sumber: f. Zapata

Ketentuan ini membuat diagonal utama dan kecil dari belah ketupat, gambar dibagi menjadi 8 segitiga identik, 4 di antaranya sesuai dengan belah ketupat, berwarna hijau, dan 4 lainnya adalah bagian dari persegi panjang. Jika 4 segitiga terakhir ini bergabung bersama, mereka akan membentuk setengah dari persegi panjang, dan 4 segitiga belah ketupat, yang lainnya.

Itu bisa melayani Anda: Segitiga Isosceles

Oleh karena itu, area belah ketupat setara dengan setengah dari area persegi panjang di mana ia terdaftar, menyatakan bahwa:

KE_berlian = A_{persegi panjang} / 2

Ini mudah diverifikasi dengan menghitung luas salah satu segitiga dan berlipat ganda dengan 4, karena mereka identik. Area segitiga apa pun adalah setengah dari produk antara pangkalan dan tingginya:

KE _{segi tiga} = basis × tinggi /2

Dari angka sebelumnya diamati bahwa dasar salah satu segitiga adalah d/2 dan tinggi d/2, yang diganti dalam formula sebelumnya memberikan:

KE _{segi tiga} = (d /2) × (d /2) /2 = (d × d) /8

Mengalikan hasil ini dengan 4 untuk memiliki area belah ketupat:

KE _berlian = 4 (D × D) /8 = (D × D) /2

Untuk bagiannya, setengah dari persegi panjang adalah:

KE _{persegi panjang} / 2 = basis × tinggi / 2

Karena dasar persegi panjang adalah D dan tingginya D, tetap: tetap:

KE_{persegi panjang} / 2 = D × D/ 2

Yang justru area belah ketupat terdaftar. Disimpulkan bahwa itu:

Area belah ketupat yang terdaftar dalam persegi panjang setara dengan setengah dari area ini.

Latihan terpecahkan

Latihan 1

Berapa area belah ketupat yang ukuran diagonal utamanya 14.6 cm dan diagonal bawah 9.8 cm?

Larutan

Dengan mengganti d = 14.6 cm dan d = 9.8 cm dalam formula area belah ketupat:

Area yang dicari adalah:

KE _berlian = 14.6 cm × 9.8 cm = 143.1 cm²

Latihan 2

Pada gambar bagian sebelumnya, diagonal utama belah ketupat yang terdaftar dalam ukuran persegi panjang d = 30 cm dan area persegi panjang bernilai 210 cm². Itu diminta untuk menghitung:

a) panjang diagonal minor

Itu dapat melayani Anda: segmen garis dan semi -river

b) Area belah ketupat, dalam dua cara: yang pertama melalui area persegi panjang dan yang kedua menggunakan formula area belah ketupat. Periksa apakah hasilnya sama.

Solusi untuk

Area persegi panjang adalah produk antara pangkalan dan tingginya. Diagonal terbesar adalah tingginya, sedangkan diagonal D terkecil akan menjadi dasar. Menggunakan rumus area dan mengganti nilai pernyataan, Anda memiliki:

KE _{persegi panjang} = basis × tinggi = d × 30 cm = 210 cm²

Maka pangkalannya layak:

D = 210 cm² / 30 cm = 7 cm

Solusi b

Seperti yang terlihat di atas, area belah ketupat adalah setengah dari area persegi panjang, dan ini diketahui:

KE _berlian = 210 cm² /2 = 105 cm²

Hasilnya diperiksa segera, mengganti dalam formula:

Diagonal sudah diketahui: D = 30 cm, d = 7 cm, lalu:

KE _berlian = 30 cm × 7 cm /2 = 105 cm²

Terbukti bahwa, seperti yang diharapkan, area belah ketupat adalah sama dalam kedua kasus.