Apa itu vektor coplanares? (Dengan latihan terpecahkan)

Itu Vektor coplanares o coplanarios adalah mereka yang terkandung di bidang yang sama. Saat Anda hanya memiliki dua vektor, ini selalu merupakan bait.

Jika Anda memiliki tiga atau lebih vektor, mungkin salah satu dari mereka tidak berada di bidang yang sama dengan yang lain, oleh karena itu mereka tidak dapat dianggap sebagai coplanares. Gambar berikut menunjukkan satu set coplanares yang dilambangkan dalam vektor tebal KE, B, C Dan D:

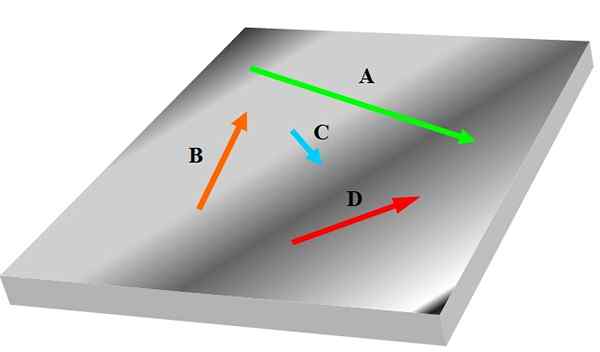Gambar 1. Empat coplanares. Sumber: Made sendiri.

Vektor terkait dengan perilaku dan sifat -sifat besaran fisik yang relevan dalam sains dan teknik; misalnya kecepatan, percepatan dan kekuatan.

Suatu gaya menghasilkan efek yang berbeda pada suatu objek ketika cara yang diterapkannya bervariasi, misalnya mengubah intensitas, arah, dan makna. Masih mengubah salah satu parameter ini hasilnya sangat berbeda.

Dalam banyak aplikasi, baik dalam statis maupun dinamika, kekuatan yang bertindak pada tubuh berada di bidang yang sama, oleh karena itu mereka dianggap coplanares.

[TOC]

Ketentuan untuk vektor menjadi coplanares

Agar tiga vektor menjadi coplanares, mereka harus berada di pesawat yang sama dan ini terjadi jika mereka memenuhi salah satu dari kondisi berikut:

-Vektor paralel, oleh karena itu komponennya proporsional dan tergantung secara linear.

-Produk campuran Anda batal.

-Jika Anda memiliki tiga vektor dan salah satu dari mereka dapat ditulis sebagai kombinasi linier dari dua lainnya, vektor ini adalah coplanares. Misalnya vektor yang dihasilkan dari jumlah dua lainnya, ketiganya semuanya berada di bidang yang sama.

Dapat melayani Anda: voltmeter: karakteristik, operasi, untuk apa, tipe

Atau, kondisi coplanarity dapat ditetapkan sebagai berikut:

U v w Mereka adalah coplanares jika ada tiga angka (skalar) α, β, γ sedemikian rupa sehingga αatau + βv + γW = 0 Dengan (α, β, γ) berbeda dari (0, 0, 0)

Produk campuran antara tiga vektor

Produk campuran antar vektor didefinisikan dengan tiga vektor atau, v Dan W, menghasilkan skalar yang dihasilkan dari melakukan operasi berikut:

atau · (v X W) = atau · (v X W)

Pertama produk silang yang ada dalam tanda kurung dibuat: v X W, yang hasilnya merupakan vektor normal (tegak lurus) ke bidang di mana mereka demikian v sebagai W.

Ya atau berada di bidang yang sama seperti v Dan W, Secara alami produk skalar (produk titik) antara U dan vektor normal tersebut harus 0. Dengan cara ini diverifikasi bahwa ketiga vektor adalah coplanares (mereka berbaring di pesawat yang sama).

Saat produk campuran tidak nol, hasilnya sama dengan volume paralelepiped yang memiliki vektor atau, v Dan W sebagai sisi yang berdekatan.

Aplikasi

Coplanares, kekuatan bersamaan dan non -kolineal

Kekuatannya bersamaan Mereka semua diterapkan pada titik yang sama. Jika mereka juga coplanares, mereka dapat digantikan hanya dengan satu, yang disebut kekuatan yang dihasilkan Dan memiliki efek yang sama dengan kekuatan asli.

Jika sebuah tubuh berada dalam keseimbangan berkat tiga coplanares, pasukan bersamaan dan non -kolineal (non -paralel), disebut KE, B Dan C, Dia Teorema Lamy Dia menunjukkan bahwa hubungan antara kekuatan -kekuatan ini (besaran) adalah sebagai berikut:

A / sin α = b / sen β = c / sen γ

Dengan α, β dan γ sebagai sudut yang menentang gaya yang diterapkan, seperti yang ditunjukkan pada gambar berikut:

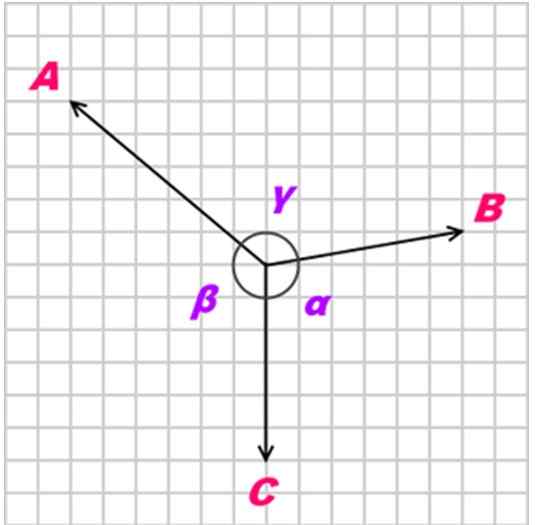Gambar 2. Tiga Kekuatan A, B dan C Coplanares bertindak atas suatu objek. Sumber: Kiwakwok di Wikipedia Inggris [domain publik]

Latihan terpecahkan

-Latihan 1

Temukan nilai k sehingga vektor berikut adalah coplanares:

Dapat melayani Anda: mesin Carnot

atau =

v =

W =

Larutan

Karena komponen vektor dimiliki, kriteria produk campuran digunakan, oleh karena itu: oleh karena itu:

atau · (v X W) = 0

Itu diselesaikan dulu v X W. Vektor akan dinyatakan dalam hal vektor unit yo, J Dan k Itu membedakan tiga arah tegak lurus dalam ruang (lebar, tinggi dan kedalaman):

v= 4 yo + J + 0 k

W= -1 yo + 2J -1 k

v X W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x J) - 2 (J x k) = 8 k + 4 J + k -2 i = -2 yo + 4 J + 9 k

Produk skalar sekarang diusulkan antara U dan vektor yang memiliki hasil dari operasi sebelumnya, operasi pencocokan ke 0:

atau · (v X W) = (-3 yo + k J + 2 k) · (-2 yo + 4 J + 9 k) = 6 + 4K +18 = 0

24 + 4K = 0

Nilai yang dicari adalah: k = - 6

Sehingga vektor atau adalah:

atau =

-Latihan 2

Gambar tersebut menunjukkan objek yang beratnya W = 600 N, tergantung pada keseimbangan berkat kabel yang ditempatkan sesuai dengan sudut yang ditunjukkan pada Gambar 3. Apakah mungkin untuk menerapkan teorema Lamy dalam situasi ini? Dalam hal apa pun temukan magnitudo T₁, T₂ Dan T₃ yang memungkinkan keseimbangan.

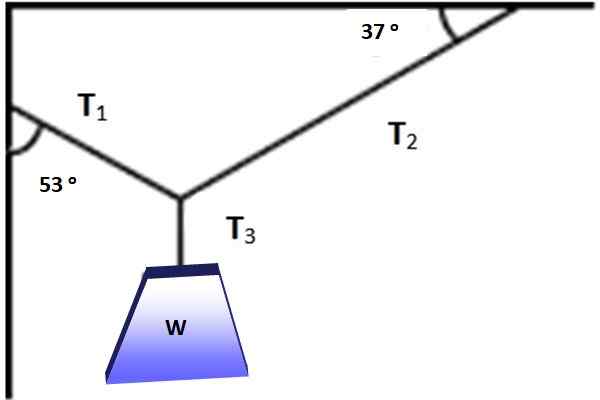Gambar 3. Bobot tergantung pada keseimbangan di bawah aksi tiga ketegangan yang ditunjukkan. Sumber: Made sendiri.

Larutan

Teorema Lamy berlaku dalam situasi ini jika simpul di mana ketiga ketegangan diterapkan dipertimbangkan, karena mereka merupakan sistem pasukan coplanar. Pertama diagram tubuh bebas dibuat untuk berat liontin, untuk menentukan besarnya t_3:

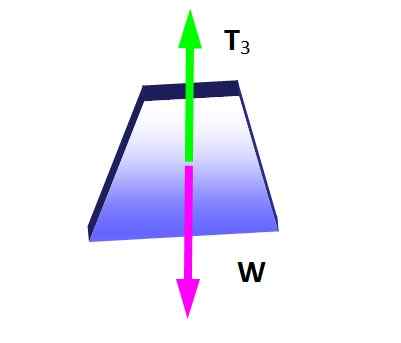Gambar 4. Diagram Tubuh Gratis untuk Menggantung Berat. Sumber: Made sendiri.

Dari kondisi keseimbangan itu mengikuti itu:

Dapat melayani Anda: difraksi suara: apa itu, contoh, aplikasi

T₃  = W = 600 n

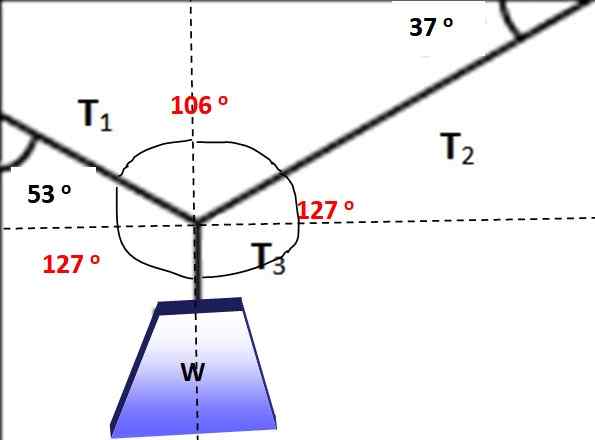
Sudut -sudut antara gaya ditandai merah pada gambar berikut, dapat dengan mudah diverifikasi bahwa jumlahnya adalah 360 °. Sekarang dimungkinkan untuk menerapkan teorema Lamy, karena salah satu kekuatan dan tiga sudut di antara mereka diketahui:

Gambar 5.- Merah sudut untuk menerapkan teorema Lamy. Sumber: Made sendiri.

T₁ / Sen 127º = w / sen 106º

Oleh karena itu: t₁ = sen 127º (w /sen 106º) = 498.5 n

Sekali lagi teorema Lamy diterapkan untuk membersihkan t₂:

T₂ / sin 127 = t₁ / Sen 127º

T₂ = T₁ = 498.5 n

Referensi

1. Figueroa, d. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. 31-68.
2. Fisik. Modul 8: Vektor. Dipulihkan dari: FRTL.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanika untuk Insinyur. Statis. Edisi ke -6. Perusahaan Editorial Kontinental.28-66.
4. McLean, w. Seri Schaum. Mekanika untuk Insinyur: Statis dan Dinamis. Edisi ke -3. Bukit McGraw. 1-15.
5. Wikipedia. Vektor. Pulih dari: itu.Wikipedia.org.