Definisi dan formula rata -rata kecepatan sudut, latihan terpecahkan

Itu Kecepatan sudut rata -rata rotasi didefinisikan sebagai sudut yang diputar oleh posisi satuan waktu vektor dari suatu titik yang menggambarkan gerakan melingkar. Bilah kipas langit -langit (seperti yang ditunjukkan pada Gambar 1), ikuti gerakan melingkar dan kecepatan rotasi sudut rata -rata dihitung dengan mengambil rasio antara sudut yang diputar dan waktu di mana sudut itu ditempuh.

Aturan yang diikuti oleh gerakan rotasi dengan cara tertentu mirip dengan kerabat gerakan translasi yang sudah ada. Jarak yang ditempuh juga dapat diukur dalam meter, namun besaran sudut mengambil relevansi khusus karena mereka sangat memfasilitasi deskripsi gerakan.

Gambar 1. Bilah kipas memiliki kecepatan sudut. Sumber: Pixabay

Huruf Yunani biasanya digunakan untuk magnitudo sudut dan huruf Latin untuk magnitudo linier yang sesuai.

[TOC]

Definisi dan Rumus

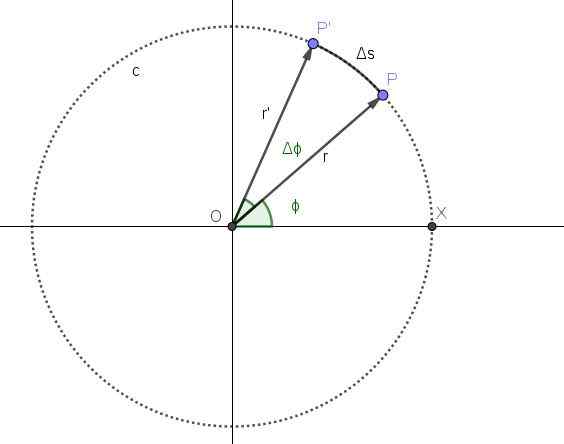
Gambar 2 mewakili pergerakan titik pada lintasan melingkar c. Posisi p dari titik sesuai dengan T instan dan posisi sudut yang sesuai dengan momen itu adalah ϕ. 

Dari saat periode waktu berlalu. Pada periode itu posisi baru dari titik adalah P 'dan posisi sudut telah meningkatkan sudut Δϕ.

Gambar 2. Pergerakan sirkular suatu titik. Sumber: Made sendiri

Kecepatan sudut rata -rata Ω adalah sudut yang ditempuh per unit waktu, sehingga hasil bagi Δϕ/Δt akan mewakili kecepatan sudut rata -rata antara momen t dan t+Δt:

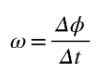
Karena sudut diukur dalam radian dan waktu dalam detik, kesatuan kecepatan sudut rata -rata adalah rad/s. Jika Anda ingin menghitung Kecepatan sudut Tepat pada saat t, maka hasil bagi Δϕ/Δt harus dihitung ketika Δt ➡0.

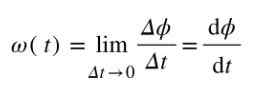Unit ukuran kecepatan sudut instan juga rad/s.

Dapat melayani Anda: 31 jenis kekuatan dalam fisika dan karakteristiknya

Rotasi seragam

Gerakan rotasi seragam jika setiap saat diamati, sudut yang ditempuh adalah sama dalam periode waktu yang sama. Jika rotasi seragam, maka kecepatan sudut kapan saja bertepatan dengan kecepatan sudut rata -rata.

Dalam gerakan rotasi yang seragam, waktu di mana belokan lengkap disebut disebut periode Dan itu dilambangkan dengan t. 

Selain itu, ketika sudut yang ditempuh penuh, 2π, jadi dalam rotasi seragam kecepatan sudut Ω terkait dengan periode t, dengan rumus berikut:

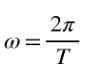
Itu frekuensi F dari rotasi yang seragam seperti rasio antara jumlah belokan dan waktu yang dihabiskan dalam bepergian, yaitu, pada saat waktu Δt ada frekuensinya:

F = n/Δt

Sebagai pangkuan (n = 1) itu dilalui dalam waktu t (periode), hubungan berikut tersedia:

F = 1/t

Yaitu, dalam rotasi yang seragam kecepatan sudut terkait dengan frekuensi melalui hubungan:

Ω = 2π ・ f

Hubungan antara kecepatan sudut dan kecepatan linier

Kecepatan linier v, Ini adalah hasil bagi antara jarak yang ditempuh dan periode waktu yang digunakan untuk menempuhnya. Pada Gambar 2 jarak yang ditempuh adalah panjang busur ΔS. 

Busur ΔS sebanding dengan sudut yang ditempuh Δϕ dan radio r, memenuhi hubungan berikut:

ΔS = r ・ Δϕ

Setiap kali Δϕ diukur dalam radian.

Jika kita membagi ekspresi sebelumnya antara periode waktu Δt kita akan memperoleh:

(ΔS/ΔT) = r ・ (Δϕ/Δt)

Rasio anggota pertama adalah kecepatan linier dan hasil bagi anggota kedua kecepatan sudut rata -rata:

Dapat melayani Anda: Gunung Olympus (Mars)

v = r ・ Ω

Latihan terpecahkan

-Latihan 1

Ujung -ujung bilah kipas atap yang ditunjukkan pada Gambar 1 bergerak dengan kecepatan 5 m/s dan bilahnya adalah radius 40 cm.

Dengan data ini menghitung: i) kecepatan sudut rata -rata roda, ii) jumlah belokan yang diberikan roda dalam satu detik, iii) periode dalam detik.

Larutan 

i) Kecepatan linier adalah V = 5 m/s.

Radio adalah r = 0,40 m.

Dari hubungan antara kecepatan linier dan kecepatan sudut, kami membersihkan yang terakhir:

V = R ・ Ω => Ω = V/R = (5 m/s)/(0,40 m) = 12,57 rad/s

ii) Ω = 2π ・ f => f = Ω / 2π = (12.57 rad / s) / (2π rad) = 2 belokan / s

iii) t = 1 / f = 1 / (2 belokan / s) = 0,5 d.

-Latihan 2

Jalan -jalan mainan bergerak di trek melingkar 2m. Pada 0s posisi sudutnya adalah 0 rad, tetapi setelah beberapa waktu posisi sudutnya

φ (t) = 2 ・ t .

Dengan data ini 

i) Hitung kecepatan sudut rata -rata dalam interval waktu berikut [0s, 0.5S]; [0.5s, 1.0s]; [1.0, 1.5s] dan akhirnya dalam periode [0.0, 1.5s]. 

ii) berdasarkan hasil bagian i) apa yang bisa dikatakan tentang gerakan?

iii) Tentukan kecepatan linier rata -rata dalam periode waktu yang sama dari Bagian I)

iv) Temukan kecepatan sudut dan kecepatan linier untuk setiap saat.

Larutan 

i) Kecepatan sudut rata -rata diberikan oleh rumus berikut:

Kami melanjutkan untuk menghitung sudut yang ditempuh dan periode waktu berlalu di setiap interval.

Interval 1: Δϕ = ϕ (0.5s) - ϕ (0.0s) = 2 (rad/s)*0.5s - 2 (rad/s)*0.0s = 1.0 rad

                   Δt = 0.5S - 0.0s = 0.5S

Dapat melayani Anda: BTU (Unit Termal): Kesetaraan, Penggunaan, Contoh

                   Ω = Δϕ/Δt = 1.0RAD/0.5s = 2.0 rad/s

Interval 2: Δϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad/s)*1.0s - 2 (rad/s)*0.5s = 1.0 rad

                   Δt = 1.0s - 0.5s = 0.5S

                   Ω = Δϕ/Δt = 1.0RAD/0.5s = 2.0 rad/s

Interval 3: Δϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*1.0s = 1.0 rad

                   Δt = 1.5S - 1.0s = 0.5S

                   Ω = Δϕ/Δt = 1.0RAD/0.5s = 2.0 rad/s

Interval 4: Δϕ = ϕ (1.5s) - ϕ (0.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*0.0s = 3.0 rad

                   Δt = 1.5S - 0.0s = 1.5S

                   Ω = Δϕ/Δt = 3.0RAD/1.5s = 2.0 rad/s

ii) Mengingat hasil sebelumnya, di mana kecepatan sudut rata -rata dihitung dalam interval waktu yang berbeda, hasil yang sama selalu diperoleh. Tampaknya menunjukkan bahwa itu adalah gerakan melingkar yang seragam. Namun, hasil ini tidak konklusif.

Cara untuk memastikan kesimpulannya adalah dengan menghitung kecepatan sudut rata -rata untuk interval sewenang -wenang [t, t -t)

                                     Δt = t ' - t

                                     Ω = Δϕ/Δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

Ini berarti bahwa jalan -jalan mainan memiliki kecepatan sudut rata -rata konstan 2 rad/s dalam periode waktu apa pun yang dipertimbangkan. Tetapi Anda dapat melangkah lebih jauh jika kecepatan sudut instan dihitung:

Ini ditafsirkan sebagai mobil mainan setiap saat memiliki kecepatan sudut konstan = 2 rad/s.

Referensi

1. Giancoli, d. Fisika. Prinsip dengan aplikasi. Edisi ke -6. Prentice Hall. 30-45.
2. Kirkpatrick, l. 2007. Fisika: Pandangan Dunia. 6^ta Edisi Singkat. Pembelajaran Cengage. 117.
3. Resnick, r. (1999). Fisik. Volume 1. Edisi ketiga dalam bahasa Spanyol. Meksiko. Perusahaan Editorial Kontinental S.KE. dari c.V. 33-52.
4. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Edisi. Meksiko. Editor Pembelajaran Cengage. 32-55.
5. Wikipedia. Kecepatan sudut. Pulih dari: wikipedia.com