Definisi Radio Konvergensi, Contoh dan Latihan Terselesaikan

Dia Radius konvergensi dari serangkaian kekuatan adalah jari -jari lingkaran konvergensi yang menjadi seri konvergen. Lingkaran ini meluas dari nilai yang membatalkan dasar kekuatan ke singularitas terdekat dari fungsi yang terkait dengan seri.

Semua fungsi analitik f (z) Itu telah mengaitkan serangkaian kekuatan di sekitar titik non -singular, yang disebut Seri Taylor:

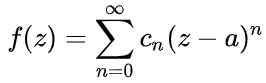
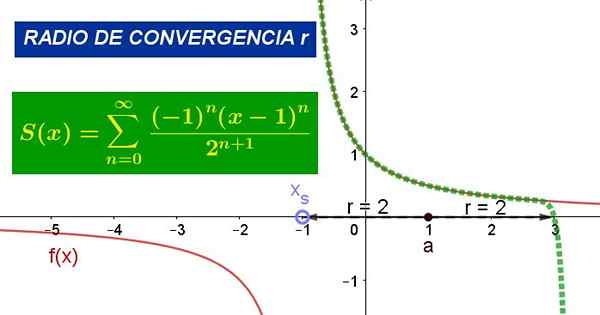
Gambar 1. Grafik menunjukkan seri daya di sekitar nilai a = 1 untuk fungsi f (x). Radius konvergensinya adalah r = 2. Sumber: Fanny Zapata.

Di mana ke Itu adalah pusat lingkaran konvergensi, z variabel independen dari fungsi dan C_N Mereka adalah koefisien yang terkait dengan yang berasal dari fungsi tersebut F pada intinya z = a.

Radius konvergensi R Ini adalah bilangan real positif yang mendefinisikan wilayah ini:

| Z - A | < r

Dimana seri konvergen. Di luar wilayah itu seri yang berbeda, yaitu, dibutuhkan nilai -nilai tak terbatas. Saat jari -jari konvergensi tidak terbatas, maka seri konvergen di seluruh bidang kompleks.

[TOC]

Bagaimana jari -jari konvergensi ditentukan?

Agar serangkaian konvergen, perlu bahwa nilai absolut dari istilah berturut -turut akan berkurang ketika jumlah istilah sangat besar. Dengan cara matematika itu akan dinyatakan sebagai berikut:

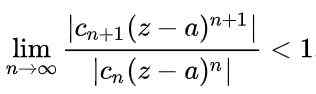
Menggunakan sifat -sifat batas dalam ekspresi sebelumnya, diperoleh:

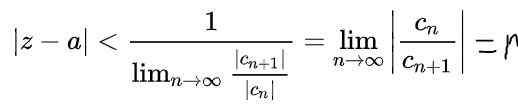
Di Sini R Itu adalah jari -jari konvergensi dan | Z - A | < r Itu adalah lingkaran perbatasan terbuka di bidang kompleks di mana seri konvergen. Dalam hal nilainya ke dan variabel z adalah bilangan real, maka interval terbuka konvergensi pada sumbu nyata adalah: (A - r, a+r).

Seri Taylor

Serangkaian fungsi Taylor f (x) Sekitar suatu nilai ke Di mana fungsi memiliki turunan tak terbatas, itu adalah serangkaian kekuatan yang didefinisikan sebagai:

Itu dapat melayani Anda: aksioma probabilitas: jenis, penjelasan, contoh, latihan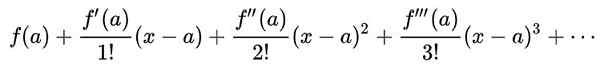

Di lingkungan | X - A | < r, dengan R sebagaiJari -jari konvergensi dari seri, seri Taylor dan fungsinya harus f (x) Mereka bertepatan.

Di sisi lain, radius konvergensi R Itu adalah jarak titik ke dan singularitasnya X_S Lebih dekat ke intinya ke, menjadi titik tunggal nilai -nilai tersebut di mana batas fungsi cenderung tak terbatas.

Itu, kapan x → x_S Jadi F → ± ∞.

Contoh

Contoh 1

Menjadi S (x) Kekuatan yang diberikan oleh ekspresi berikut:

S (x) = 1 - x + x²- X³+ X⁴-.. .+(-1)^N ⋅ x^N +.. .

Untuk menentukan wilayah di mana seri konvergen, kami menghitung hasil bagi antara istilah (n-beeimo + 1) dan istilah (n-emem):

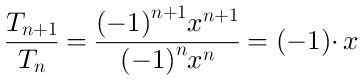
Nilai absolut dari hasil bagi anterior adalah | x | dan batasnya saat N → ∞ itu juga  | x |.

Agar seri ini menjadi konvergen, perlu bahwa:

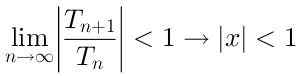
Jadi jari -jari konvergensi dari seri ini adalah R = 1, karena itu menyatu untuk nilai x yang berada pada jarak kurang dari 1 sehubungan dengan pusat x = 0.

Contoh 2

Anda ingin menemukan serangkaian fungsi Taylor f (x) = 1 / (1 + x) sekitar titik x = 0 dan tentukan jari -jari konvergensi.

Untuk menemukan seri, kami mengambil turunan berturut -turut dari fungsi f (x), yang akan kami tunjukkan tiga yang pertama:

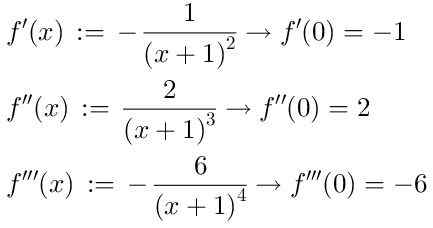
Dengan mempertimbangkan bahwa istilah nol urutan dari seri Taylor adalah:

 f (0) = 1,

Urutan pertama: F '(0)/1!

Pesanan kedua:

 F "(0)/2!

Urutan ketiga:

 f "(0)/3!

Dan seterusnya, seri Taylor dari fungsi yang diberikan adalah:

f (x) = 1 - x + x² - X³ + X⁴ -.. .+(-1)^N ⋅ x^N +.. .

Dapat melayani Anda: segitiga sama sisi: karakteristik, sifat, formula, area

Itu bertepatan dengan seri Power yang dipelajari dalam Contoh 1.

Kami telah mengatakan bahwa jari -jari konvergensi dari seri Taylor adalah jarak dari pusat ekspansi dalam seri, yang dalam kasus kami adalah nilainya x = 0 Sampai singularitas fungsi pertama f (x). 

Karena fungsi kami memiliki singularitas (yaitu, tak terhingga) di x = -1, Jarak antara nilai -1 dan pusat ekspansi 0 adalah | -1 - 0 | = 1, Disimpulkan bahwa jari -jari konvergensi seri Taylor 1.

Hasil ini sepenuhnya bertepatan dengan yang diperoleh dalam Contoh 1 dengan metode lain.

Fakta bahwa zona konvergensi seri Taylor adalah interval terbuka (-1, 1) menyiratkan bahwa fungsi dan seri bertepatan dalam interval ini, tetapi tidak di luar yang sama.

Yang ditunjukkan pada Gambar 2, di mana 41 istilah seri Taylor telah diambil, ditarik oleh garis biru kontinu, sedangkan fungsi asli ditampilkan pada garis merah segmen.

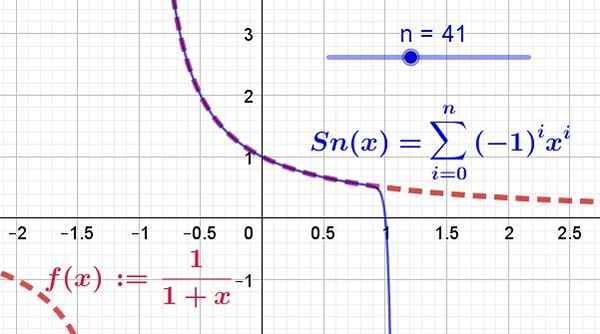Gambar 2. Fungsi f (x) (berwarna merah) dan serangkaian kekuatannya (atau seri Taylor dengan warna biru) ditampilkan. Ini dapat dilihat sebagai 41 istilah pertama dari seri konvergen antara -1 dan 1. Selain itu fungsi dan seri hanya bertepatan di wilayah konvergensi. (Sumber: Fanny Zapata)

Latihan terpecahkan

- Latihan 1

Pertimbangkan fungsi yang sama f (x) = 1 / (1 + x) Contoh 2, tetapi kali ini diminta untuk menemukan seri fungsi Taylor di sekitar titik A = 1.

Larutan

Kami menemukan istilah seri berturut -turut, dimulai dengan istilah independen yaitu f (1) = ½.

Koefisien berikutnya yang sesuai dengan istilah urutan pertama adalah:

F '(1)/1! = -¼

Urutan kedua adalah:

f "(1)/2! = 2/(2³ 2!)

Ikuti koefisien urutan ketiga:

Itu bisa melayani Anda: tetradecágon

f "(1)/3! = -6 / (2⁴ 3!)

Dan seterusnya. Seri Taylor akan menjadi:

Sf (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Latihan 2

Temukan jari -jari konvergensi dari seri sebelumnya

Larutan

Kami menulis istilah n-eme dan istilah n-alkaus lebih banyak:

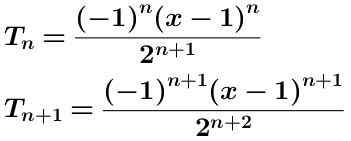Kami menghitung hasil bagi dua istilah ini yang ditunjukkan di bawah ini disederhanakan:

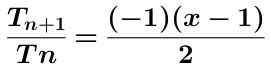
Nilai absolut dari ekspresi sebelumnya diambil dengan mendapatkan:

| X - 1 | / 2

Namun, untuk seri konvergen, perlu bahwa jumlah sebelumnya lebih rendah dari unit, yaitu:

| X - 1 | < 2

Yang menunjukkan bahwa jari -jari konvergensi di sekitar nilai x = 1 adalah:

R = 1

Di sisi lain, ekspresi sebelumnya setara dengan ketidaksetaraan ganda:

-2 < x - 1 < +2

Jika kita menambahkan +1 ke masing -masing dari tiga anggota dari ekspresi sebelumnya, itu diperoleh:

-1 < x < 3

Yang merupakan interval konvergensi seri.

Gambar 1 menunjukkan fungsi asli dan seri Taylor dari fungsi tersebut di sekitar titik x = 1. Pada gambar dapat diverifikasi bahwa seri bertepatan dengan fungsi dalam lingkungan titik x = 1, tetapi dalam radius konvergensi.

Referensi

1. Yayasan CK-12. Seri Daya: Representasi Fungsi dan Operasi. Dipulihkan dari: CK12.org.
2. Engler, a. 2019. Kalkulus integral. Universitas Nasional Pantai.
3. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
4. Teks Matematika Gratis. Seri Kekuatan. Pulih dari: matematika.Liibretexts.org.
5. Wikipedia. Seri Kekuatan. Pulih dari: is.Wikipedia.org.
6. Wikipedia. Radius konvergensi. Diperoleh dari: di.Wikipedia.org