Alasan Trigonometrik Contoh, Latihan, dan Aplikasi

Itu alasan trigonometri Mereka adalah quotient atau alasan yang dapat dilakukan dengan nilai sisi segitiga siku. Sisi ini adalah: dua kategori yang membentuk 90º dengan satu sama lain dan hipotenuse, yang membentuk sudut akut θ dengan salah satu kategori.

6 Quotients dapat dibentuk. Nama mereka dan singkatan masing -masing adalah:

• Brease (Sen)
• Coseno (cos)
• Tangent (TG atau TAN)
• Cotangent (CTG atau COTA)
• Secante (detik) dan
• Harvester (Harmony)

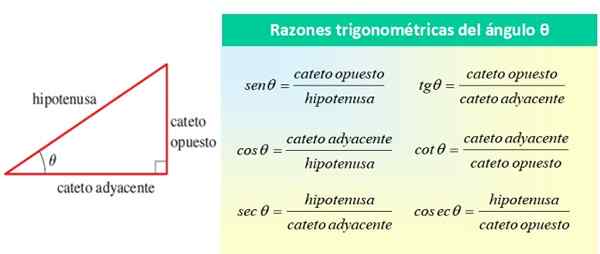
Semuanya merujuk pada sudut θ, seperti yang ditunjukkan pada gambar berikut:

Gambar 1. Alasan trigonometri sudut akut θ. Sumber: f. Zapata.

Alasan trigonometri dasar sudut θ adalah sin θ, cos θ dan tan θ, sedangkan alasan yang tersisa dapat dinyatakan dalam ketiganya. Dari gambar sebelumnya Anda dapat melihat itu:

• Dtk θ = 1/ cos θ
• Harm θ = 1/ sin θ
• cot θ = 1/tg θ

Ukuran sisi segitiga tidak mempengaruhi nilai alasannya, karena dua segitiga yang sudutnya mengukur sama adalah segitiga yang sama dan kutipan masing -masing di antara sisi memiliki nilai yang sama.

[TOC]

Contoh

Misalnya, mari kita hitung alasan trigonometri sudut θ di segitiga berikut:

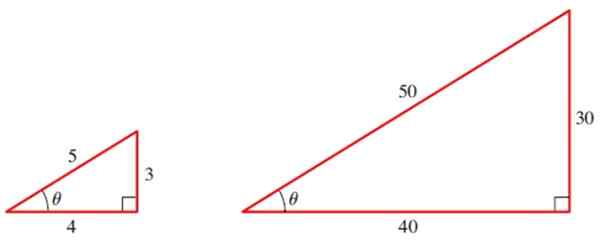Gambar 2. Dua segitiga serupa memiliki alasan trigonometri yang sama dari sudutnya. Sumber: Stewart, J.PRECCCULMENT: Matematika untuk Perhitungan.

Untuk segitiga kecil kami memiliki tiga alasan dasar sudut θ:

sin θ = 3/5

cos θ = 4/5

tg θ = ¾

Dan sekarang mari kita menghitung tiga alasan dasar θ dengan segitiga besar:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

Detail penting yang perlu dipertimbangkan adalah sebagai berikut: Baik sin θ dan cos θ kurang dari 1, karena kategori selalu mengukur kurang dari hipotenuse. Memang:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Latihan terpecahkan

Dalam latihan berikut, ia diminta untuk menyelesaikan segitiga kanan, yang berarti menemukan panjang ketiga sisi dan ukuran sudut internalnya, salah satunya selalu berukuran 90º.

Dapat melayani Anda: Persamaan -Degree Pertama: Formula, Cara menyelesaikannya, Contoh, Latihan

Teorema Pythagoras berlaku untuk segitiga persegi panjang dan sangat berguna ketika dua sisi diketahui dan yang hilang harus ditentukan. Teorema mengatakan:

Sisi miring² = Cateto yang berlawanan² + Cateto yang berdekatan²

Kita dapat memverifikasi teorema Pythagoras dengan segitiga kecil Gambar 2, yang kakinya 3 dan 4. Urutan di mana kategori diambil tidak masalah. Menerapkan teorema yang kami miliki:

Sisi miring² = 3² + 4² = 9 + 16 = 25

Oleh karena itu penggunaan hipoten adalah:

Hypotenuse = √25 = 5

- Latihan 1

Hitung alasan trigonometri sudut yang ditunjukkan pada segitiga berikut:

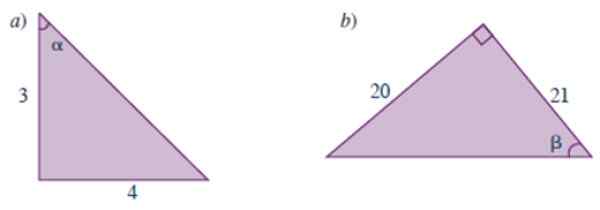Gambar 3.- Segitiga untuk tahun ini diselesaikan 1. Sumber: carena, m. 2019. Manual Matematika Preuniversity.

Solusi untuk

Segitiga ini sama pada Gambar 3, tetapi mereka meminta kami alasan trigonometri dari sudut akut lainnya, dilambangkan α. Pernyataan itu tidak menawarkan nilai hypotenusa, bagaimanapun, dengan penerapan teorema Pythagoras kita tahu bahwa itu bernilai 5.

Alasannya dapat dihitung langsung dari definisi, berhati -hati saat memilih kaki yang merupakan kebalikan dari sudut α untuk menghitung sen α. Mari kita lihat:

• sin α = 4/5
• cos α = 3/5
• TG α = 4/3
• cot α = ¾
• SEC α = 1/(3/5) = 5/3
• Harm α = 1/(4/5) = 5/4

Dan seperti yang bisa kita lihat, nilai -nilai alasan trigonometri telah dipertukarkan. Memang, α dan θ adalah sudut yang saling melengkapi, yang berarti mereka menambahkan 90º. Dalam hal ini dipenuhi bahwa sen α = cos θ dan seterusnya untuk alasan lainnya.

Solusi b

Mari kita menghitung hipotenus dari segitiga melalui teorema Pythagoras:

Sisi miring² = 20² + dua puluh satu² = 841

√841 = 29

Maka 6 alasan trigonometri sudut β adalah:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• Cot β = 21/20
• SEC β = 1/(21/29) = 29/21
• Harm β = 1/(20/29) = 20/29

Dapat melayani Anda: Operasi gabungan

- Latihan 2

a) Temukan nilai x dalam gambar.

b) Hitung perimeter dari 3 segitiga yang ditampilkan.

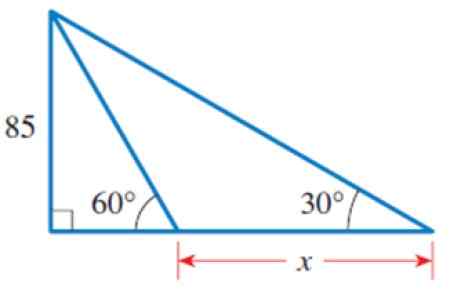Gambar 4. Segitiga untuk tahun ini diselesaikan 2. Sumber: Stewart, J. PRECCCULMENT: Matematika untuk Perhitungan.

Solusi untuk

Pada gambar kita dapat mengidentifikasi beberapa segitiga, khususnya segitiga persegi panjang dari kiri, yang memiliki kategori sama dengan 85 dan sudut akut 60º.

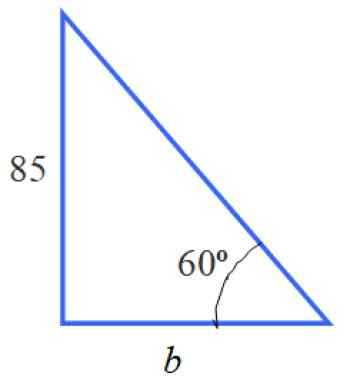Gambar 5. Segitiga di sebelah kiri.

Dengan informasi segitiga ini kita dapat menghitung sisi b. Bukan ukuran yang ditanyakan oleh pernyataan itu, tetapi mengetahui nilainya adalah langkah sebelumnya.

Untuk menentukan alasan yang tepat adalah TG 60 º = 85 /B, karena B adalah kaki yang berdekatan dengan 60 ° dan 85 adalah sebaliknya dengan sudut tersebut. Karena itu:

B = 85 / tg 60º = 85 / √3

Setelah diketahui B, kita akan menggunakan segitiga persegi panjang besar dan luar, yang memiliki sisi umum dengan segitiga sebelumnya: yang berukuran 85. Ini adalah cateto yang bertentangan dengan sudut 30º.

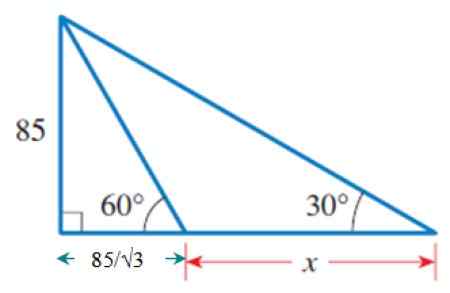Gambar 6. Segitiga Luar, di mana bagian dari pangkalan sudah diketahui.

Dari sana:

Cateto berdekatan dengan 30º = (85/√3) + x

Sekarang kita dapat meningkatkan yang berikut:

85 / [(85 / √3) + x] = tg 30º

Apa yang ada di braket persegi melipatgandakan 30º TG:

85 = [(85/√3) + x]. TG 30º

Menerapkan properti distributif perkalian:

85 = TG 30º. (85/√3) + x. TG 30º

Karena itu:

X.TG 30º = 85 - TG 30º. (85/√3) = 85 [1 - TG 30º . (1/√3)] = 85 . (2/3) = 170/3

Mengganti nilai TG 30º = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.limabelas

Solusi b

Perimeter segitiga kecil

Menjadi h₁ Segitiga hypotenuse dari segitiga ini, yang dapat dihitung dengan teorema Pythagoras atau melalui alasan trigonometri, misalnya cos 60º:

cos 60 º = 85 / √3 / h₁→ H₁ = (85/√3) ÷ cos 60º = 98.1

Untuk menemukan P, perimeter segitiga ini, kami cukup menambahkan 3 sisi:

Dapat melayani Anda: statistik deskriptif: sejarah, karakteristik, contoh, konsep

P = 85 + (85/√3) + 98.1 = 232.2

Perimeter segitiga eksternal

Menjadi h₂ ke hypotenuse dari segitiga eksternal:

Sen 30º = 85 ÷ h₂  

H₂ = 85 ÷ dosa 30º = 170

Untuk segitiga ini perimeter adalah:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Perimeter segitiga non -rectangle

Dari segitiga ini kita sudah tahu semua sisinya:

P = x + h₁ + H₂ = 98.15 + 98.15 + 170 = 366.3

Aplikasi alasan trigonometri

Alasan trigonometri memiliki banyak aplikasi praktis, misalnya ketinggian dapat dihitung.

Misalkan menara air berjarak 325 kaki dari sebuah bangunan. Seorang pengamat yang terletak di jendela mencatat bahwa sudut ketinggian ujung atas menara adalah 39 º, sedangkan sudut depresi yang dengannya dasar menara terlihat 25º. Keajaiban:

a) Berapa ketinggian menara?

b) Berapa Jendela?

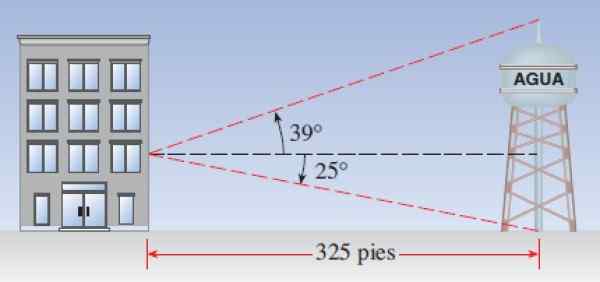Gambar 7. Skema untuk menghitung ketinggian vista torre dari sebuah bangunan. Sumber: Stewart, J. PRECCCULMENT: Matematika untuk Perhitungan.

Solusi untuk

Dari kateto yang berlawanan dengan 39 dari segitiga atas kita mendapatkan bagian dari jawabannya:

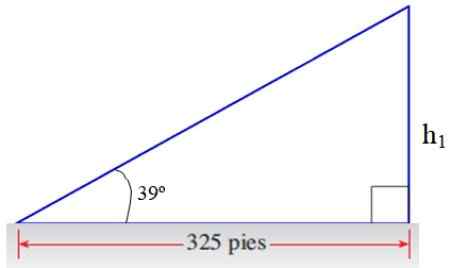Angka 8. Segitiga untuk Latihan Aplikasi. Sumber: f. Zapata.

H₁/325 = TG 39º → H₁ = 325 . TG 39º kaki = 263.2 kaki

Dengan cara yang sama kita mendapatkan sisa ketinggian menara, yang disebut h₂ Dari segitiga bawah:

H₂/325 = TG 25º → H₂ = 325 . TG 25º kaki = 151.6 kaki

Tinggi total menara adalah H₁ + H₂ = 263.2 + 151.6 kaki = 414.7 kaki.

Solusi b

Jendela justru pada ketinggian h₂ tanah:

H₂ = 151.6 kaki.

Referensi

1. Carena, m. 2019. Manual Matematika Preuniversity. Universitas Nasional Pantai.
2. Hoffman, J. Pemilihan masalah matematika. Volume 3.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.