Fisik

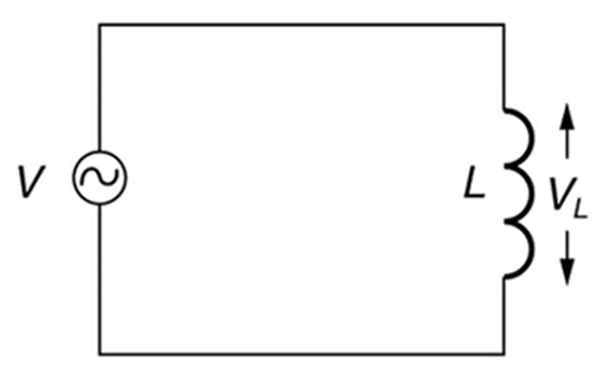
Reaktansi induktif

Reaktansi induktif
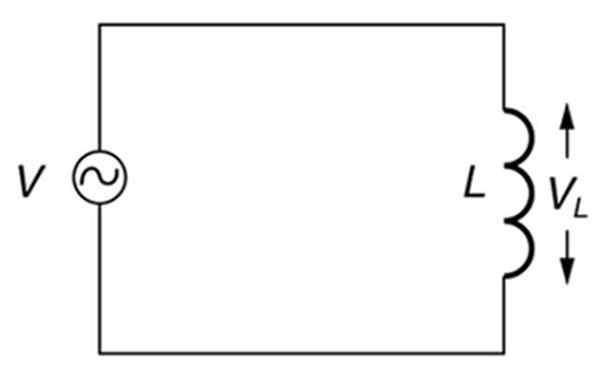Sirkuit alternatif yang murni induktif. Sumber: buka stax. Fisika Perguruan Tinggi.

Apa reaktansi induktif?

Itu Reaktansi induktif Itu mengacu pada oposisi yang disajikan oleh koil ke bagian arus, di sirkuit alternatif. Dengan kata lain, itu adalah kemampuan penginduksi untuk mengurangi arus di sirkuit alternatif. Dilambangkan sebagai xL, Nilainya tergantung pada induktansi dan frekuensi sudut tegangan:

XL= Ω ∙ l

Di mana Ω adalah frekuensi sudut dalam radian/s dan induktansi L, diukur dalam henrios (h) dalam sistem unit internasional jika.

Induktansi besar menghasilkan reaktansi induktif yang besar, karena ketahanan terhadap perubahan lebih besar. Dan reaktansi juga meningkat dengan frekuensi, sehingga induktansi tertentu L akan menghasilkan reaktansi yang lebih besar, semakin tinggi frekuensi tegangan.

Unit reaktansi induktif adalah ohmio, dilambangkan dengan Ω. Itu adalah unit resistensi listrik yang sama, tetapi tidak seperti ini, xL Itu tidak konstan, karena tergantung pada frekuensi tegangan alternatif yang diterapkan.

Oleh karena itu, dalam suatu sirkuit yang satu -satunya elemen adalah sumber alternatif dan induktansi (sirkuit induktif), seperti yang ditunjukkan pada gambar di atas, reaktansi induktif akan tergantung pada frekuensi sumber.

Namun, analogi XL Dengan ketahanan listrik dapat diperluas ke sirkuit induktif, memungkinkan penerapan hukum Ohm. Jika x didefinisikanL sebagai rasio antara amplitudo tegangan vL Di induktor, dan saya saat iniL yang melintasinya:

XL = VL / YOL

Anda dapat menulis undang -undang OHM untuk sirkuit induktif murni sebagai berikut:

VL = XL∙ iL

Rumus reaktansi induktif

Untuk menghitung reaktansi induktif, formula yang diberikan pada awal digunakan, di mana L mewakili induktansi (Henrios) dan Ω adalah frekuensi sudut (radian/kedua):

Dapat melayani Anda: Millikan Eksperimen: Prosedur, Penjelasan, Pentingnya

XL= Ω ∙ l

Adalah umum untuk frekuensi diekspresikan dalam Hertz atau Hertzio (Hz). Dalam hal ini, itu dilambangkan dengan F dan terkait dengan frekuensi sudut melalui rumus:

Ω = 2π ∙ f

Dalam hal ini, reaktansi dihitung sebagai:

XL= 2πf ∙ l

Dalam salah satu formula ini, reaktansi induktif menghasilkan ohm, seperti yang dijelaskan sebelumnya.

Efek induktansi pada sirkuit induktif

Karena induktansi menentang perubahan atau variasi arus, reaktansi induktif ditandai dengan menunda gelombang arus sehubungan dengan gelombang tegangan.

Dalam grafik berikut, yang menunjukkan tegangan vL (Biru) dan saat ini iL (merah) dalam induktor, keduanya sinoidally, diamati bahwa kedua gelombang sudah ketinggalan zaman 90º. Mulai dari t = 0, nilai tegangan maksimum, namun, arusnya nol pada saat itu.

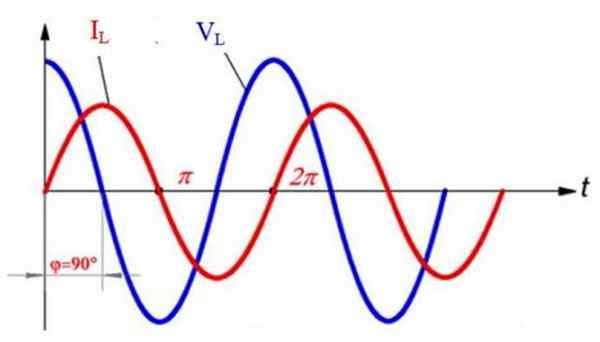Arus dan tegangan alternatif dalam sirkuit induktif. Disiapkan oleh: f. Zapata.

Kemudian, diamati bahwa arus mencapai nilai maksimum pada t = π /2, tetapi pada saat itu tegangan dibatalkan dan menginvestasikan polaritasnya, yaitu menjadi negatif. Secara bersamaan, arus mengurangi nilainya, sedangkan tegangan menjadi semakin negatif.

Selanjutnya, pada t = π, tegangan mencapai besarnya maksimum, meskipun dengan polaritas terbalik, dan kemudian arus dibatalkan. Dari semua ini, maka setiap kali vL Itu mencapai puncak, arus dibatalkan, dan setiap kali arus mencapai besarnya maksimum, tegangannya 0.

Arus selalu mencapai puncaknya setelah tegangan melakukannya, dan ini karena, seperti yang dinyatakan pada awalnya, induktansi menentang meningkat atau berkurang.

Dapat melayani Anda: Keuntungan Mekanik: Formula, Persamaan, Perhitungan, dan Contoh

Cara menghitung reaktansi induktif

Menghitung reaktansi induktif sangat sederhana: perlu untuk mengetahui nilai induktansi dan frekuensi tegangan alternatif yang diterapkan. Kemudian, data ini diganti dalam salah satu rumus yang diberikan di bagian sebelumnya dan operasi yang sesuai dilakukan.

Contoh -contoh berikut dan latihan terselesaikan menunjukkan cara melakukannya dalam berbagai situasi.

Contoh

Contoh 1

Misalkan induktor L = 5 mH, di mana tegangan frekuensi alternatif diterapkan 60.0 Hz. Reaktansi induktif dalam kasus ini dihitung oleh:

XL= 2πf ∙ l

Tetapi sebelum mengganti nilai, induktansi harus menjadi Henrios, dikalikan dengan faktor 1 × 10−3. Karena itu:

L = 5 × 10−3 H

Jadi:

XL= 2πf ∙ l = xL= 2π × 60 Hz × 5 × 10−3 H = 1. 88 ohm

Contoh 2

Sekarang induktansi yang sama terhubung ke tegangan frekuensi alternatif yang berbeda: 10.0 kHz. Dalam hal ini, induktansi menyajikan reaktansi yang lebih besar:

XL= 2πf ∙ l = xL= 2π × 10.0 × 103 Hz × 5 × 10−3 H = 314.2 ohm

Contoh 3

Tegangan yang diterapkan pada induktansi Contoh 1 dan 2 memiliki nilai 120 V RMS. Arus RMS masing -masing ditentukan melalui hukum OHM VL = XL∙ iL:

yoL = VL / XL

Untuk frekuensi 60.0 Hz, arusnya adalah:

yoL = 120 V / 1. 88 ohm = 63.8 a

Dan untuk frekuensi 10.0 kHz:

yoL = 120 V / 314.2 ohm = 0.38 a

Karena dalam kasus terakhir reaktansi jauh lebih besar, diharapkan arus akan lebih kecil. Properti ini menjadikan induktor filter frekuensi tinggi, fitur yang digunakan untuk mengurangi suara frekuensi tinggi dalam peralatan suara, atau untuk melindungi perangkat dari UPS arus mendadak, di antara aplikasi lainnya.

Dapat melayani Anda: Teorema Steiner: Penjelasan, Aplikasi, Latihan

Latihan terpecahkan

Latihan 1

Tentukan reaktansi induktif di sirkuit yang terdiri dari induktansi 2.5 mh, secara seri dengan sumber tegangan alternatif, yang frekuensinya 75 r.P.M.

Larutan

Revolusi atau siklus lengkap sama dengan 2π radian, dan satu menit memiliki 60 detik, oleh karena itu, frekuensi 75 r.P.M setara dengan:

75 r.P.M = 75 × 2π radian / 60 detik = 7.85 radian/s

Dan dengan nilai ini, reaktans adalah:

XL= Ω ∙ l = (7.85 radian/s) × 2.5 × 10−3 H = 0.02 Ω

Latihan 2

Induktansi serial digunakan dengan sumber komputer untuk memfilter kebisingan dari frekuensi tinggi.

a) Apa yang seharusnya menjadi nilai induktansi minimum yang diperlukan untuk menghasilkan reaktansi 2 kΩ, jika frekuensi sinyal yang disaring adalah 15 kHz?

b) Temukan reaktansi induktor ini pada frekuensi 60 Hz.

Solusi untuk

XL = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Oleh karena itu, pembersihan persamaan xL= 2πf ∙ l, Anda memiliki:

L = xL / 2π ∙ f = 2000 Ω / 2π × 15000 Hz = 0.0212 H = 21.2 mh

Solusi b

Menggunakan x lagiL= 2πf ∙ l, tetapi dengan f = 60 Hz, hasilnya:

XL= 2π × 60 Hz × 0.0212 h = 8 ohm.

Referensi

  1. Bauer, w. (2011). Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 
  2. Giancoli, d. (2006). Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
  3.  Katz, d. (2013). Fisika untuk Ilmuwan dan Insinyur. Yayasan dan Koneksi. Pembelajaran Cengage.
  4. Buka Stax. Fisika Perguruan Tinggi. Diperoleh dari: OpenStax.org.
  5. Sears, z. (2016). Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 2. Pearson