Aturan korespondensi suatu fungsi

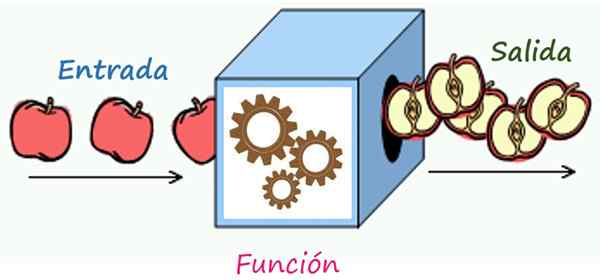
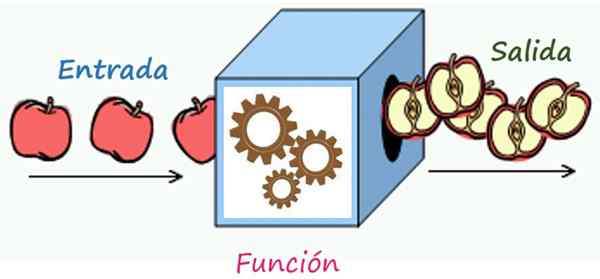Aturan korespondensi adalah mekanisme yang mengubah elemen masuk ke dalam elemen output. Sumber: Wikimedia Commons/F. Zapata

Apa aturan korespondensi suatu fungsi?

Itu aturan korespondensi suatu fungsi Tunjukkan cara elemen satu set terkait dengan unsur -unsur lain. Elemen set pertama dikenal sebagai domain, dan untuk yang kedua, seperti Kodominium salah satu kontradominium.

Hubungan atau tautan antar set dapat ditentukan dengan instruksi verbal atau tertulis, namun, ketika set adalah numerik, aturan korespondensi ditunjukkan oleh rumus.

Formula ini berisi operasi yang harus dilakukan dengan elemen rakitan awal, dan dengan demikian mendapatkan serangkaian elemen yang termasuk dalam kodominium.

Sekarang, ketika hubungan antara elemen adalah fungsi, aturan korespondensi memenuhi dua kondisi khusus:

• Ke masing -masing elemen domain dikaitkan, melalui aturan korespondensi, satu elemen kodominium, yang dikenal sebagai gambar.
• Gambar ini unik, dengan kata lain, tidak ada elemen domain yang dikaitkan dengan lebih dari satu elemen kodominium.

Dengan cara ini, Anda dapat membayangkan aturan korespondensi suatu fungsi sebagai mekanisme yang terkunci dalam sebuah kotak. Setiap nilai domain, tanpa kecuali, dapat memasukkan kotak dan keluar dari itu diubah, melalui operasi yang ditunjukkan oleh aturan korespondensi. Contohnya akan segera dilihat.

Contoh

Contoh 1

Aturan korespondensi suatu fungsi dapat dinyatakan sebagai instruksi tertulis, ketika elemen tidak numerik.

Misalnya, ada satu set negara, dilambangkan sebagai P, dan satu set kota lain C:

Itu dapat melayani Anda: u -test mann - Whitney: apa itu dan saat diterapkan, eksekusi, contoh

P = Kanada, Meksiko, Spanyol, AS, Prancis, Argentina, Brasil, Jerman

C = Paris, London, Buenos Aires, Berlin, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Roma, Brasilia, Toronto

Jadilah aturan korespondensi F Antara P dan C yang diberikan oleh:

F: P → c

Di mana F Itu adalah aturannya "... siapa modal itu .. ”, Yang mengaitkan masing -masing negara di P (set awal), dengan ibu kota di C (set kedatangan).

Misalnya: “Spanyol, yang modal siapa Madrid". Elemen "Spanyol" milik set p start, dan elemen "madrid" ke seluruh C, kedatangan.

Representasi fungsi ini dapat dilakukan melalui diagram Venn atau hanya melalui pasangan yang dipesan.

Pasangan yang dipesan berisi, sesuai namanya, dua elemen dengan urutan tertentu, dalam contoh ini, elemen pertama dari pasangan ini adalah negara, dan yang kedua, ibukotanya.

Untuk bagiannya, diagram Venn adalah cara untuk memvisualisasikan fungsi, menunjukkan set awal dan kedatangan, serta aturan korespondensi di antara mereka.

Representasi F as yang dipesan

F = (Kanada, Ottawa); (Meksiko, Mexico City); (Spanyol Madrid); (AS; Washington); (Paris, Prancis); (Argentina Buenos Aires); (Brasil Brasilia); (Jerman, Berlin)

Pasangan pertama Associates Canada, yang modal siapa Ottawa, rekan kedua Meksiko, yang modal siapa Mexico City dan sebagainya.

Representasi F sebagai Diagram Venn

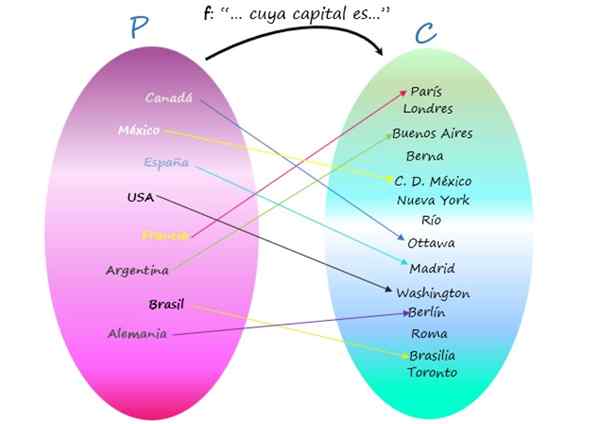
Perhatikan bahwa ada kota -kota yang bukan ibukota negara mana pun, karena, meskipun mereka adalah elemen kodominium, mereka bukan gambar dari elemen apa pun dari set awal. Meski begitu, hubungannya adalah fungsi, karena yang penting adalah bahwa masing -masing negara memiliki modalnya, dan ini unik.

Dapat melayani Anda: area pentagon biasa dan tidak teratur: bagaimana itu diambil, latihan

Subset yang dibentuk oleh elemen kodominium yang merupakan gambar beberapa elemen domain, disebut rentang atau fungsi fungsi. Sebagai contoh, rute r F adalah:

R = Paris, Buenos Aires, Mexico City, Ottawa, Madrid, Berlin, Washington, Brasilia

Perlu bertanya apakah hubungan antara C dan P dapat dibangun, di mana C menjadi set awal dan kedatangan. Jawabannya adalah ya, tetapi itu bukan fungsi, karena ada kota -kota yang bukan ibukota, seperti New York, atau negara yang modal mereka tidak muncul di antara unsur -unsur kompleks P, seperti Roma.

Contoh 2

Ketika set keberangkatan dan set kedatangan adalah numerik, aturan korespondensi fungsi yang menghubungkannya adalah rumus. Misalnya, jadilah penguasaan fungsi set berikut:

D = 0, 1, 2, 3, 4, 5, 6)

Aturan korespondensi F: D → r yang menghubungkan elemen D dengan himpunan bilangan real R adalah:

F: "Dobel"

Jika "X" adalah elemen dari set awal, F (x) adalah elemen yang sesuai dari set kedatangan, dan aturan korespondensi ditulis seperti ini:

f (x) = 2x

Kodominium adalah himpunan bilangan real. Subset dari REAIS adalah rute fungsi ini, set angka yang nilainya dua kali lebih dari x:

R = 0, 2, 4, 6, 8, 10, 12

Dalam bentuk pasangan yang dipesan, aturan korespondensi menghasilkan:

F = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Pasangan yang dipesan bisa menjadi grafik di pesawat Cartesian. Elemen pertama torsi ditempatkan pada sumbu horizontal, juga disebut sumbu absis atau sumbu "x", sedangkan yang kedua terjadi pada sumbu vertikal, sumbu dari sumbu yang dipesan atau hanya "y":

Dapat melayani Anda: properti distributif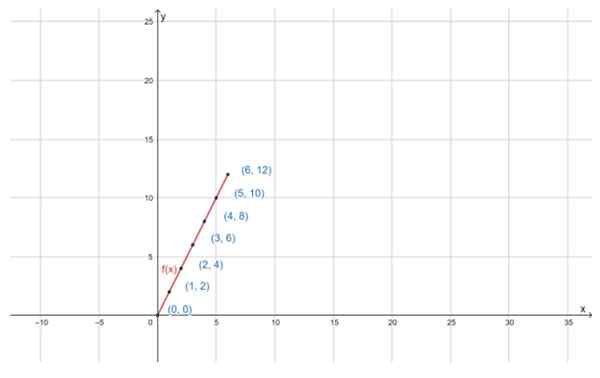 Grafik fungsi f (x) = 2x, untuk domain d yang ditentukan, adalah garis lurus. Sumber: f. Zapata melalui Geogebra

Latihan

Tentukan aturan korespondensi untuk hubungan berikut, menunjukkan apakah itu fungsi atau tidak. Himpunan bilangan alami adalah n dan yang nyata adalah r.

Juga menunjukkan domain, kodominium dan rute fungsi, dalam kasus -kasus di mana ia sesuai:

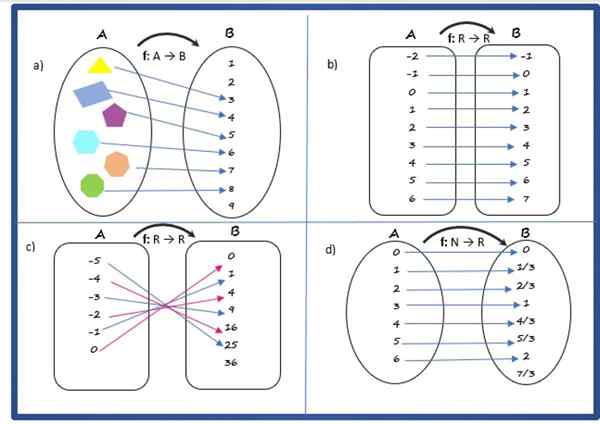
Solusi untuk

Ini adalah fungsi, karena setiap elemen set awal, yang terdiri dari poligon, memiliki gambar yang unik dalam set kedatangan.

Aturan korespondensi menghubungkan poligon dengan jumlah sisinya, domain terdiri dari set A dari poligon:

A = Triangle, Quadrilateral, Pentagon, Hexagon, Heptagon, Octagon

Kodominium adalah himpunan bilangan alami pertama, termasuk 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Dan CO C adalah bilangan alami dari 3 hingga 8:

C = 3, 4, 5, 6, 7, 8

Solusi b

Itu adalah fungsi, karena memenuhi persyaratan yang ditentukan di atas.

Aturan korespondensi adalah:

f (x) = x + 1

Aturan korespondensi menunjukkan bahwa fungsi ditentukan oleh r → r, oleh karena itu, domain adalah himpunan bilangan real. Dan co -oominium dan rute juga bertepatan dengan yang asli.

Solusi c

Ini adalah fungsi, dengan aturan korespondensi:

f (x) = x²

Domain dan kodominium adalah set reais, tetapi rute hanya terdiri dari bilangan real positif, dilambangkan sebagai r⁺ dan termasuk 0.

Solusi d

Itu adalah fungsi. Aturan korespondensi adalah:

f (x) = x/3

Domainnya adalah himpunan bilangan alami N dan kodominium, serta rute, adalah angka N nyata R.