Aturan Tangan Kanan

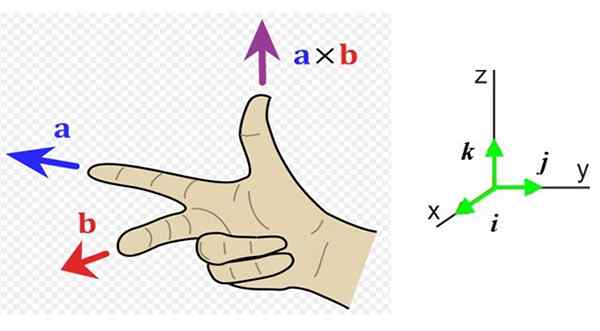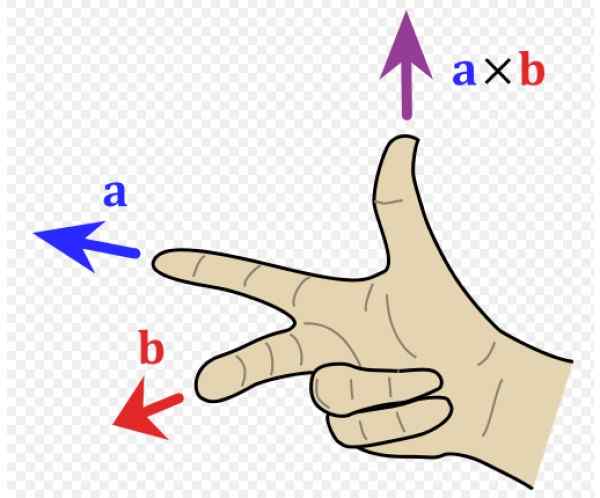
Gambar 1. Aturan Tangan Kanan. Sumber: Wikimedia Commons. ACDX [CC BYS-S (http: // createveCommons.Org/lisensi/by-sa/3.0/]].

Apa aturan tangan kanan?

Itu Aturan Tangan Kanan Ini adalah sumber mnemonik untuk menetapkan arah dan arah vektor yang dihasilkan dari produk vektor atau produk silang. Ini banyak digunakan dalam fisika, karena ada besaran vektor penting yang merupakan hasil dari produk vektor. Begitulah kasus torsi, gaya magnet, momentum sudut dan momen magnetik, misalnya.

Menjadi dua vektor generik ke Dan B Produk silang siapa ke X B. Modul vektor semacam itu adalah:

ke X b = ke.B.dosa α

Di mana α adalah sudut minimum antara ke Dan B, Sementara A dan B mewakili modul mereka. Untuk membedakan vektor dari modul mereka, huruf tebal digunakan.

Sekarang kita perlu mengetahui arah dan makna vektor ini, jadi lebih mudah untuk memiliki sistem referensi dengan tiga arah ruang (Gambar 1 kanan). Vektor unit yo, J Dan k Mereka masing -masing menunjuk ke pembaca (di luar halaman), ke kanan dan ke atas.

Dalam contoh Gambar 1, vektor ke sedang menuju ke kiri (alamat Dan Jari negatif dan telunjuk tangan kanan) dan vektor B Pergi ke pembaca (alamat X positif, jari tengah tangan kanan).

Vektor yang dihasilkan ke X B memiliki arah ibu jari, ke arah z positif.

Aturan kedua tangan kanan

Aturan ini banyak digunakan ketika ada besaran yang arah dan maknanya berputar, seperti medan magnet B diproduksi oleh kawat tipis dan bujursangkar yang mengangkut arus.

Dalam hal ini, garis medan magnet adalah keliling konsentris dengan kawat, dan arah belokan diperoleh dengan aturan ini sebagai berikut: ibu jari kanan menunjukkan arah arus dan empat jari yang tersisa melengkung ke arah arah arah lapangan. Kami mengilustrasikan konsep pada Gambar 2.

Dapat melayani Anda: guncangan elastis: dalam dimensi, kasus khusus, latihan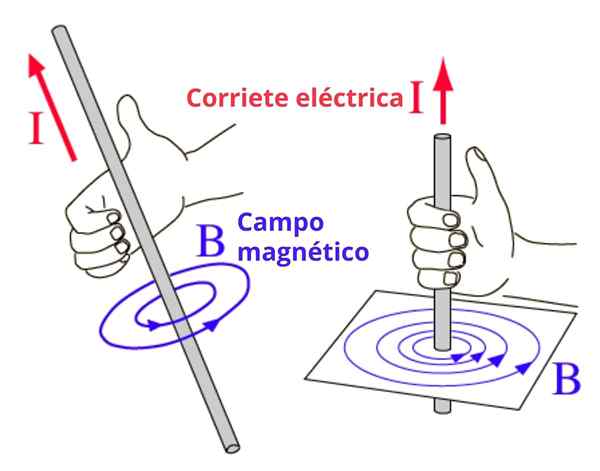Gambar 2. Aturan Tangan Kanan untuk menentukan arti sirkulasi medan magnet

Aturan alternatif tangan kanan

Gambar berikut menunjukkan bentuk alternatif dari aturan kanan. Vektor yang muncul dalam Pencerahan adalah:

• Kecepatan v dari beban tepat waktu itu.
• Medan magnet B di mana beban bergerak.
• F_B Gaya yang diberikan medan magnet pada beban.

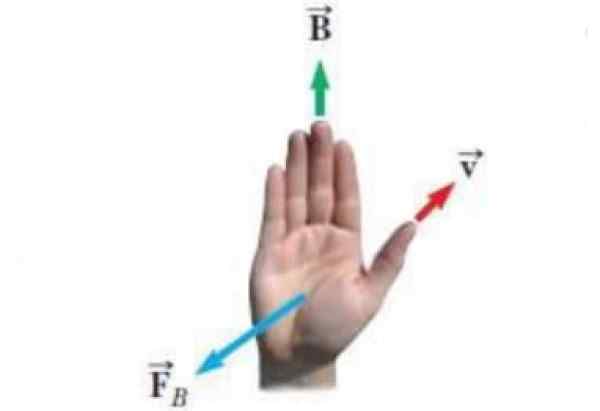Gambar 3. Aturan alternatif tangan kanan. Sumber: Wikimedia Commons. ExperticUis [CC BY-SA (https: // createveCommons.Org/lisensi/by-sa/4.0)]

Persamaan untuk gaya magnet adalah F_B = qv X B dan aturan tangan kanan untuk mengetahui arah dan rasa F_B Ini berlaku seperti ini: poin jempol menurut V, empat jari yang tersisa ditempatkan sesuai dengan bidang B. Jadi F_B Itu adalah vektor yang keluar dari telapak tangan, tegak lurus terhadapnya, seolah -olah mendorong beban.

Perhatikan itu F_B akan menunjuk ke arah yang berlawanan jika beban yang negatif, karena produk vektor tidak komutatif. Nyatanya:

ke X B = - b X ke

Aplikasi

Aturan tangan kanan dapat diterapkan pada berbagai besaran fisik, mari kita tahu beberapa di antaranya:

Kecepatan dan percepatan sudut

Keduanya kecepatan sudut Ω Seperti akselerasi sudut α Mereka adalah vektor. Jika suatu objek berputar di sekitar sumbu tetap, ada kemungkinan kecepatan sudut Ω.

Untuk bagiannya percepatan sudut α akan memiliki alamat yang sama dengan Ω, Tapi artinya tergantung pada jika Ω meningkatkan atau mengurangi besarnya dari waktu ke waktu. Dalam kasus pertama, keduanya memiliki arah dan makna yang sama, tetapi di detik mereka akan memiliki indera yang berlawanan.

Dapat melayani Anda: watt law: apa itu, contoh, aplikasi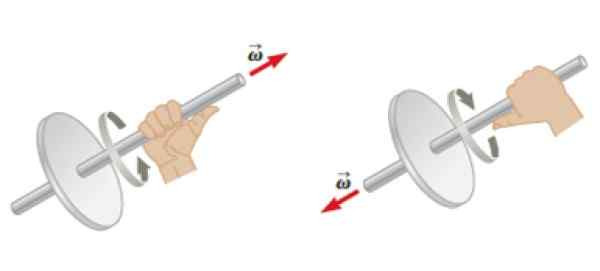Gambar 4. Aturan tangan kanan diterapkan pada objek dalam rotasi untuk menentukan arah dan arah kecepatan sudut. Sumber: Serway, R. Fisik.

Momentum sudut

Vektor sudut L_{SALAH SATU} dari partikel yang berputar di sekitar sumbu tertentu atau didefinisikan sebagai produk vektor dari vektor posisi instannya R  dan jumlah gerakan linier P:

L = R X P

Aturan kanan diterapkan dengan cara ini: jari telunjuk ditempatkan dalam arah dan arah yang sama R, Jari tengah di P, keduanya pada bidang horizontal, seperti pada gambar. Secara otomatis ibu jari meluas secara vertikal ke atas yang menunjukkan arah dan arah momentum sudut L_{SALAH SATU.}

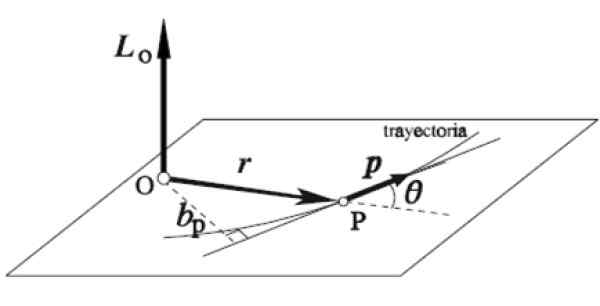Gambar 5. Vektor sudut. Sumber: Wikimedia Commons.

Latihan

Latihan 1

Putar Gambar 6 berjalan cepat dengan kecepatan sudut Ω dan sumbu simetrinya rusak lebih lambat di sekitar sumbu vertikal z. Gerakan ini disebut presesi. Jelaskan kekuatan yang bertindak pada putaran dan efek yang mereka hasilkan.

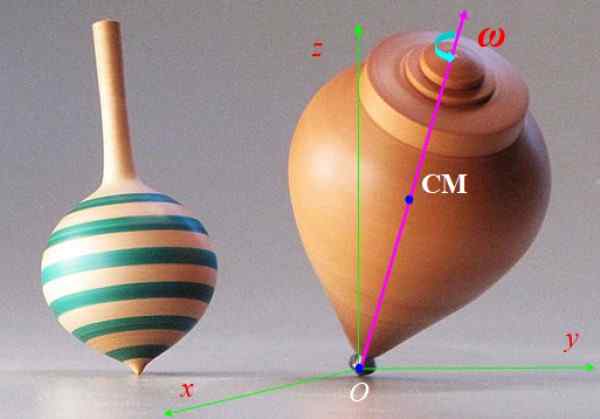Gambar 6. Putaran putaran. Sumber: Wikimedia Commons.

Larutan

Kekuatan yang bekerja pada putaran itu normal N, diterapkan pada titik dukungan dengan tanah atau lebih berat mG, diterapkan di tengah massa cm, dengan G Vektor akselerasi keparahan, diarahkan ke bawah secara vertikal (lihat Gambar 7).

Kedua kekuatan itu seimbang, oleh karena itu putaran tidak bergerak. Namun berat menghasilkan torsi atau torsi τ Bersih tentang poin atau, diberikan oleh:

τ_{SALAH SATU} = R_{SALAH SATU} X F, dengan F = MG.

Sebagai R dan mG Mereka selalu berada di pesawat saat putaran berbelok, sesuai dengan aturan tangan kanan torsi τ_{SALAH SATU} Itu selalu terletak di pesawat Xy, tegak lurus keduanya a R sebagai G.

Perhatikan itu N tidak menghasilkan torsi sehubungan dengan O, karena vektornya R Tentang atau nol. Torsi itu menghasilkan perubahan dalam momentum sudut yang menyebabkan presesi putaran di sekitar sumbu z.

Dapat melayani Anda: Saldo Termodinamika: Kelas dan Aplikasi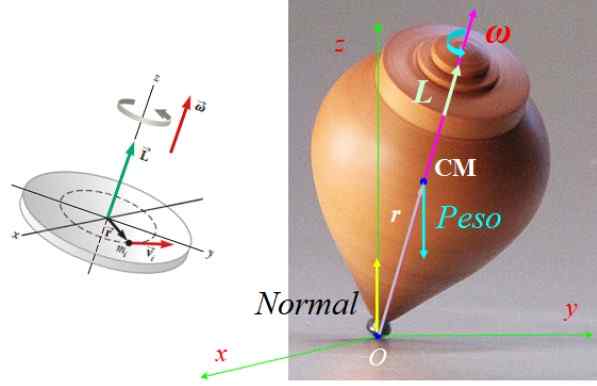Gambar 7. Kekuatan yang bekerja pada putaran dan vektor momentum sudutnya. Sumber figur kiri: Serway, R. Fisika untuk Sains dan Teknik.

Latihan 2

Tunjukkan arah dan arah vektor momentum sudut L dari Trumpe dari Gambar 6.

Larutan

Titik putaran apa pun memiliki massa m_yo, kecepatan v_yo dan posisi vektor R_yo, Saat berputar di sekitar sumbu z. Momentum sudut L_yo dari partikel tersebut adalah:

L_yo = R_yo X P_yo = R_yo x m_yov_yo

Mengingat R_yo Dan v_yo Mereka tegak lurus, besarnya L adalah:

L_yo = m_yoR_yov_yo

Kecepatan linier v terkait dengan kecepatan sudut Ω melalui:

v_yo = r_yoΩ

Karena itu:

L_yo = m_yoR_yo (R_yoΩ) = m_yoR_yo²Ω

Momentum sudut total dari trompo l adalah jumlah momentum sudut masing -masing partikel:

L = (∑m_yoR_yo² ) Ω

∑ m_yoR_yo²  Ini adalah momen inersia I putaran, lalu:

L= IΩ

Karena itu L Dan Ω Mereka memiliki arah dan makna yang sama, seperti yang ditunjukkan pada Gambar 7.