Aturan tuas

Apa aturan tuas?

Itu aturan tuas Ini adalah prosedur matematika yang memungkinkan untuk menghitung fraksi, persentase atau jumlah fase yang ada dalam keseimbangan dalam sistem biner. Tidak hanya matematika, tetapi juga cukup grafis dan tegas, menjadi sangat berguna dalam perhitungan fisikokimia dan teknik.

Aturan ini berlaku untuk diagram fase untuk sistem biner, terlepas dari jenis sistem itu sendiri. Artinya, fase bisa solid, seperti halnya paduan; atau cair dan gas, seperti yang kita lihat dalam sistem dalam keseimbangan uap cair.

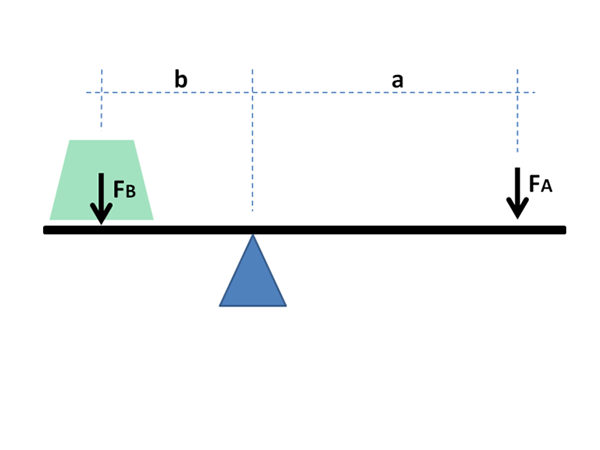
Prinsip fisik dan matematika tuas juga digunakan untuk tujuan kimia dan dalam fisika material. Sumber: Jimbowley, CC BY-SA 3.0, via Wikimedia Commons

Aturan tuas dapat diterapkan secara langsung dengan mempertimbangkan grafik nilai dalam sumbu absis, di mana fraksi global atau persentase komponen yang paling mudah menguap biasanya terjadi, dalam kasus cairan; atau refraktori, dalam kasus logam dalam paduan mereka.

Seperti yang akan dilihat di bawah ini, namanya adalah karena kesamaan besar yang dimilikinya dengan ekspresi matematika yang menunjukkan keseimbangan antara dua massa yang terletak di ujung rocker dengan fulcro.

Lengan tuas harus menyeimbangkan untuk menyeimbangkan massa beban; Dalam kasus diagram fase, fraksi dan mol fase dalam keseimbangan material.

Penjelasan

Aspek grafis

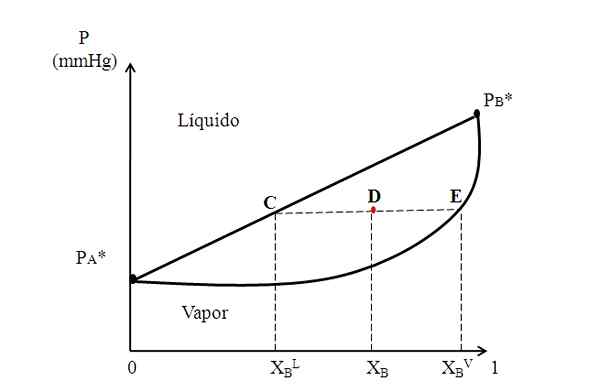Diagram biner hipotetis di mana garis pengikat menunjukkan komposisi fase cairan dan uap. Sumber: Gabriel Bolívar.

Di tengah diagram di atas kami memiliki wilayah di mana cairan dan uap hidup berdampingan; yaitu wilayah keseimbangan uap cair. Di atas wilayah ini campuran A dan B akan menjadi cair, dan di bawahnya akan menjadi soda karena tekanan yang lebih rendah.

Sekarang, pertimbangkan campuran dengan komposisi x_B dan yang tekanannya memposisikannya pada titik D. Kami menarik dari titik D garis horizontal yang menyentuh garis dan kurva di sisi, masing -masing titik yang berasal dari C dan E. Baris ini, yang mengkomunikasikan titik-titik C, D dan E, C-D-E, adalah yang dikenal sebagai garis persatuan, dan dengan memproyeksikannya ke arah sumbu dan harus memberi kita tekanan sistem.

Itu dapat melayani Anda: alkalinitas air: apa itu, tekad dan kepentingan

Kemudian, dari titik -titik ini kami menggambar garis lain yang tegak lurus terhadap garis pengikat, yang akan memainkan sumbu x. Saat titik E bertumpu pada kurva uap, maka kita akan memiliki fraksi molar b dalam fase uap (x_B^V). Demikian juga, titik C, pada garis lurus cairan, akan memberi kita fraksi molar B dalam fase cair (x_B^L).

Aturan tuas didasarkan pada garis pengikat, dan jarak antara x_B^L, X_B dan x_B^V.

Pengurangan matematika

Fraksi molar global B sama dengan:

X_B = N_B / (N^L + N^V)

Di mana N_B Mereka adalah mol total B baik dalam fase cairan dan uap, dan N^L Dan N^V adalah mol masing -masing untuk fase ini. Membersihkan N_B kami akan memiliki:

N_B = X_BN^L + X_BN^V (1)

Di samping itu, N_B Itu juga sama dengan:

N_B = N_B^L + N_B^V

= X_B^LN^L + X_B^VN^V  (2)

Sekarang menyamakan persamaan (1) dan (2) akan memberi kita:

X_BN^L + X_BN^V = X_B^LN^L + X_B^VN^V

Dan mengatur ulang:

N^L(X_B - X_B^L) = N^V(X_B^V - X_B) (3)

N^L(C-d) = N^V(DARI)

Dua ekspresi matematika terakhir ini adalah aturan tuas. Perhatikan bahwa x_B - X_B^L Itu adalah jarak antara titik C dan D; dan x_B^V - X_B, Ini adalah jarak antara titik D-E: dua bagian dari garis pengikat (lengan tuas).

Persamaan ini sangat mirip dengan yang menggambarkan keseimbangan massa pada rocker dengan fulcro:

M₁l₁ = m₂l₂

Dengan demikian, aturan tuas akan memungkinkan kita untuk menghitung total mol N^L Dan N^V asalkan total mol campuran diketahui, N_T (N_T = N^L + N^V).

Bentuk kedua

Ekspresi sebelumnya untuk aturan tuas berfungsi untuk menghitung jumlah (massa, mol, dll.) dari fase dalam keseimbangan. Namun, versi aturan tuas yang paling terkenal memungkinkan kita untuk menghitung fraksi atau persentase dari setiap fase, hanya mengambil jarak antara x_B, X_B^L dan x_B^V.

Pertimbangkan sistem yang sama di atas, memiliki bentuk lain dari aturan tuas:

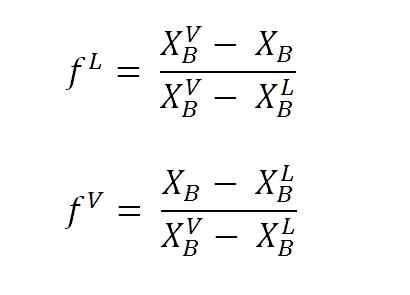Persamaan untuk menghitung fraksi cairan dan uap menggunakan lengan tuas. Sumber: Gabriel Bolívar.

Di mana F ^L Dan F ^VMereka adalah fraksi molar (atau persentase, tergantung pada grafik) dari fase cairan dan uap. Perhatikan itu, jelas, F ^L Dan F ^V Mereka tidak memiliki unit; ketika N^L Dan N^V Ya, mereka memiliki unit (tahi lalat, gram, dll.).

Dapat melayani Anda: panas reaksi

Contoh

Metode 1

Dalam wadah 28 mol B dan 12 mol dari A dicampur. Tentukan jumlah dan fraksi molar untuk fase yang terbentuk.

Kami menghitung x_B:

X_B = (28 mol B)/ (28 mol B + 12 mol A)

= 0.7

Nilai ini sesuai dengan x_B dari diagram teratas. Intersepsi akan memberi kita kira -kira nilai -nilai berikut untuk x_B^L dan x_B^V:

X_B^L = 0.41

X_B^V = 0.94

Dengan aturan tuas:

N^L(X_B - X_B^L) = N^V(X_B^V - X_B)

Dan mengetahui itu N_T = N^L + N^V, Dan? N_T = 40 mol, lalu kita jelas N^L salah satu N^V tergantung yang lain:

N^L(X_B - X_B^L) = (40 mol - N^L) (X_B^V - X_B)

Mengatur ulang dan membersihkan N^L kami akan memiliki:

N^L = (40 mol) (x_B^V - X_B) / (X_B^V - X_B^L)

Bukankah ungkapan ini ingat itu F ^L? Sekarang mengganti yang akan kita miliki:

N^L = (40 mol) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 mol dalam fase cair

Kita bisa menghitung N^V Dalam dua cara:

N^V = N^L(X_B - X_B^L) / (X_B^V - X_B)

salah satu

N^V = 40 mol - 18.11 mol

= 21.89 mol dalam fase uap

Metode 2

Bagaimana jika kita menghitung dulu F ^L Dan F ^V?

F ^L = (X_B^V - X_B) / (X_B^V - X_B^L)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 atau 45.28%

Yaitu, 45.2% dari tahi lalat berada dalam fase cair, menjadi jumlah yang sama dengan:

N^L = F ^LN_T

= (0.4528) (40 mol)

= 18.11 mol

DAN F ^V Kita dapat menghitungnya secara setara dalam dua cara:

F ^V = 1 - F ^L

salah satu

F ^V = (X_B - X_B^L) / (X_B^V - X_B^L)

Menjadi nilainya:

F ^V = 0.5472 atau 54.72%

Dan maka dari itu, N^V Itu akan sama dengan:

N^V = F ^VN_T

= (0.5472) (40 mol)

= 21.89 mol

Perhatikan bahwa menerapkan dua bentuk aturan tuas sebagai metode perhitungan alternatif, hasil yang sama dapat dicapai. Metode 2 tampaknya lebih langsung dan sederhana; tetapi jika diamati dengan hati -hati, setelah pembersihan diselesaikan N^L salah satu N^V, Akan terlihat bahwa kedua metode itu sebenarnya sama mudahnya.

Latihan terpecahkan

Selanjutnya, dua latihan lainnya akan diselesaikan, di mana sekarang sistem yang dipertimbangkan akan melibatkan cairan-padat dan non-cair-uap. Juga, diagram grafik sehubungan dengan suhu sistem dan bukan tekanannya.

Latihan 1

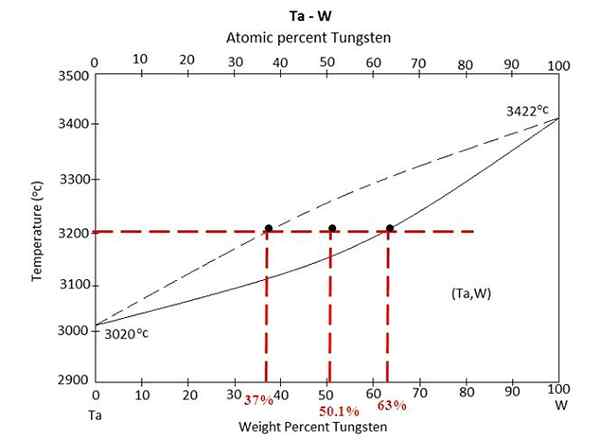Diagram fase untuk paduan antara tantalo dan tungsten. Sumber: Materialpedia, CC BY-SA 4.0, via Wikimedia Commons

Kami memiliki diagram fase di atas paduan antara tantalo dan tungsten, ta-w. Pada sumbu x persentase massa global tungsten, w% (m/m) diwakili.

Di dalam wilayah keseimbangan cair (TA+W) dan padat (paduan) ada campuran pada 3200 ºC. Tentukan massa dari setiap fase dengan asumsi bahwa 100 gram paduan dipanaskan.

Itu dapat melayani Anda: logam, non -logam dan metaloid

Prosedur

Kali ini latihan akan diselesaikan dengan menggunakan bentuk kedua dari aturan tuas. Garis Union memberi tahu kita bahwa: dalam fase padat kita memiliki 63% tungsten, sedangkan dalam fase cair kita memiliki 37% tungsten. Ini karena tungsten meleleh ke suhu yang lebih tinggi (3422 ºC) daripada tantal (3020 ºC).

Jadi kita punya:

W%^S atau w_S= 63%

W%^L atau w_L= 37%

Dan juga:

W₀ = 50.1%

Kami menerapkan aturan tuas untuk F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 atau 49.61%

Perhatikan bahwa jarak yang sesuai dengan fase cair adalah lengan tuas di dekat fase padat, sisi berlawanan dari titik medium.

Massa fase cair karena itu:

(0.4961) (100 gram) = 49.61 gram cair

Dan fase padat akan sama dengan:

100 gram - 49.61 gram = 50.39 gram paduan kaya tungsten

Latihan 2

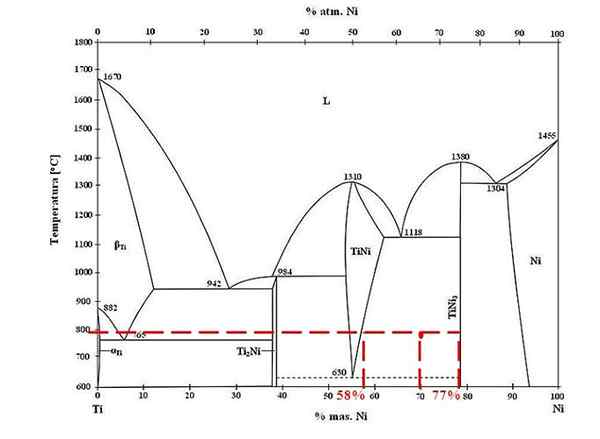Diagram fase untuk paduan titanium-nickel. Sumber: Doomgiver, CC BY-SA 3.0, via Wikimedia Commons

Untuk paduan titanium dan nikel pada 800 ºC, dan dengan 70% nikel, tentukan berapa banyak tini dan tini₃ mereka hadir.

Prosedur

Kali ini mereka hanya meminta fraksi massa dari setiap fase. Titik merah terletak di daerah kesetimbangan antara fase tini dan tini₃, yang kurva berada di tempat ia memainkan garis persatuan yang mengalir ke nilai 58% atau untuk fase tini, dan 77% atau untuk fase tini₃.

Perhatikan bahwa titik merah lebih dekat ke fase tini₃ bahwa fase tini. Ini berarti harus ada lebih banyak tini₃ tini itu; Dan karena itu, jarak atau lengan tuas yang sesuai dengan tini₃ Itu harus menjadi yang terpanjang, sebaliknya (70%-58%).

Mengetahui hal ini, kami melanjutkan untuk menghitung F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 atau 63.16%

Memang, 63.16% dari paduan sesuai dengan fase tini₃. Sementara itu, fase tini sesuai dengan:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 atau 36.84%

Sebagai kesimpulan dari latihan yang diangkat, kita dapat mengatakan bahwa aturan tuas sangat membantu untuk menentukan fraksi setiap fase dalam kesetimbangan untuk sistem dua komponen.

Referensi

1. Walter J. Moore. (1963). Kimia Fisik. Dalam Kinetika Kimia. Edisi Keempat, Longmans.
2. Iran. Levine. (2009). Prinsip -prinsip fisikokimia. Edisi Keenam. MC Graw Hill.
3. Wikipedia. (2020). Aturan tuas. Diperoleh dari: di.Wikipedia.org
4. Michael Adewumi. (18 Mei 2020). Aturan tuas. Pulih dari: eng.Librettexts.org
5. Adam Warren. (1997). Diagram fase: garis pengikat dan aturan tuas. Pulih dari: Southampton.Ac.Inggris
6. Universitas Cambridge. (2020). Aturan tuas. Diperoleh dari: Doitpoms.Ac.Inggris