Aturan Sarrus

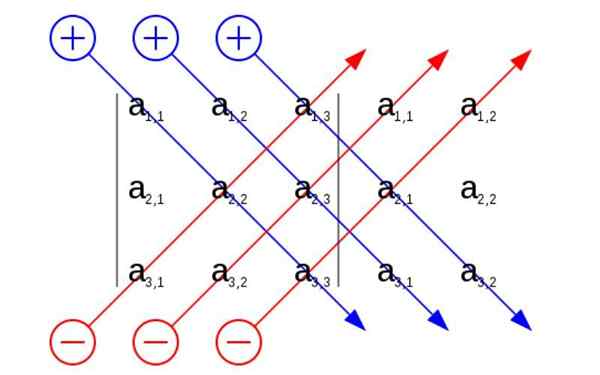
Aturan Sarrus. Sumber: Pengguna: Sevela.P, CC BY-SA 4.0, Wikimedia Commons

Apa aturan Sarrus?

Itu Aturan Sarrus Ini adalah teknik untuk menghitung penentu matriks persegi 3 × 3 atau lebih. Sistem ini memungkinkan solusi menjadi lebih mudah. Ini juga digunakan untuk menentukan apakah set vektor secara linear independen dan membentuk dasar ruang vektor.

Aplikasi ini didasarkan pada inversibilitas matriks. Jika matriks biasa, penentu berbeda dari 0. Jika tunggal, penentu bernilai 0. Penentu hanya dapat dihitung dalam matriks persegi.

Untuk menghitung matriks dari urutan apa pun, teorema Laplace dapat digunakan. Teorema ini memungkinkan kita untuk menyederhanakan matriks dimensi tinggi, dalam jumlah penentu kecil yang kita rusak dari matriks utama.

Menyatakan bahwa penentu suatu matriks sama dengan jumlah produk dari setiap baris atau kolom, dengan penentu matriks yang terpasang.

Ini mengurangi penentu, sehingga penentu derajat N, menjadi penentu N-1. Jika kami menerapkan aturan ini secara berurutan, kami dapat memperoleh penentu dimensi 2 (2 × 2) atau 3 (3 × 3), di mana perhitungannya jauh lebih mudah.

Aturan Sarrus

Pierre Frederic Sarrus (1798-1861) adalah ahli matematika Prancis. Sebagian besar perjanjian matematika didasarkan pada metode resolusi persamaan dan perhitungan variasi, dalam persamaan numerik.

Dalam salah satu perjanjiannya, ia memecahkan salah satu teka -teki mekanik yang paling kompleks. Untuk memecahkan masalah karya yang diartikulasikan, Sarrus memperkenalkan transformasi gerakan bujursangkar alternatif, dalam gerakan melingkar yang seragam. Sistem baru ini dikenal sebagai mekanisme Sarrus.

Itu dapat melayani Anda: eksternalisasi dan internalisasi biaya

Penelitian yang memberinya yang paling banyak adalah yang ia memperkenalkan metode baru untuk menghitung faktor penentu, dalam artikel "Metode Nouvelles menuangkan la résolution des équations" ("Metode Baru untuk Resolusi Persamaan"), yang diterbitkan pada tahun 1833. Cara menyelesaikan persamaan linier ini dikenal sebagai Sarrus Rule.

Aturan Sarrus memungkinkan untuk menghitung penentu matriks 3 × 3, tanpa menggunakan teorema Laplace, memperkenalkan metode yang lebih sederhana dan lebih intuitif. 

Untuk dapat memverifikasi nilai aturan Sarrus, kami mengambil matriks dimensi 3:

Perhitungan penentu akan dibuat oleh produk diagonal utamanya, mengurangi produk dari diagonal terbalik. Ini akan menjadi berikut:

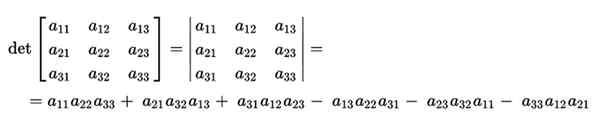
Aturan Sarrus memungkinkan kita untuk mendapatkan penglihatan yang jauh lebih sederhana saat menghitung diagonal penentu. Itu akan disederhanakan dengan menambahkan dua kolom pertama ke bagian belakang matriks.

Dengan cara ini, lebih jelas tentang diagonal utamanya dan yang terbalik, untuk perhitungan produk.

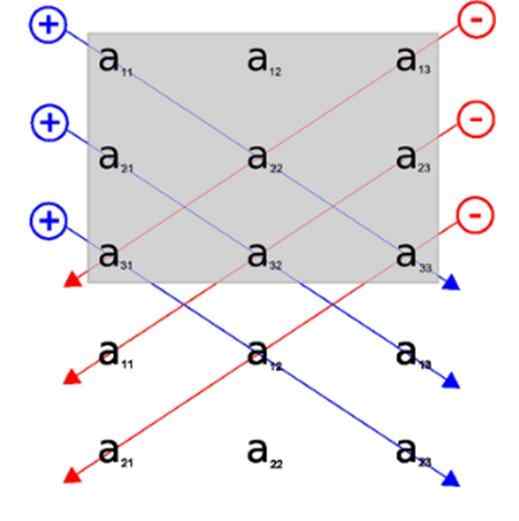
Melalui gambar ini kita dapat melihat penerapan aturan Sarrus, kami menyertakan baris 1 dan 2, di bawah representasi grafis dari matriks awal. Dengan cara ini, diagonal utama adalah tiga diagonal yang muncul di tempat pertama.

Tiga diagonal terbalik, pada gilirannya, adalah yang pertama kali muncul di belakang.

Dengan cara ini, diagonal muncul dengan cara yang lebih visual, tanpa menyulitkan resolusi penentu, mencoba mencari tahu elemen matriks apa yang dimiliki masing -masing diagonal.

Dapat melayani Anda: kata -kata quechua diterjemahkan ke dalam bahasa Spanyol

Seperti yang terlihat pada gambar, kami memilih diagonal dan menghitung produk yang dihasilkan dari setiap fungsi. Diagonal yang muncul dengan warna biru adalah yang bertambah. Dengan jumlah ini, kami mengurangi nilai diagonal yang muncul dengan warna merah.

Agar kompresi lebih mudah, kita dapat menggunakan contoh numerik, alih -alih menggunakan istilah aljabar dan istilah subter.

Jika kita mengambil matriks 3 × 3, misalnya:

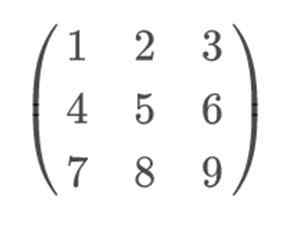
Untuk menerapkan aturan Sarrus, dan menyelesaikannya dengan cara yang lebih visual, kita harus menyertakan baris 1 dan 2, masing -masing sebagai baris 4 dan 5. Penting untuk mempertahankan baris 1 di posisi ke -4, dan baris 2 di 5. Karena jika kita menukarnya, aturan Sarrus tidak akan efektif.

Untuk menghitung penentu, matriks kami adalah sebagai berikut:

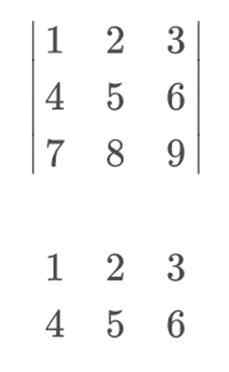
Untuk melanjutkan perhitungan, kami akan melipatgandakan elemen diagonal utama. Keturunan yang mereka mulai di sebelah kiri akan membawa tanda positif, sedangkan diagonal terbalik, yang merupakan yang dimulai di sebelah kanan, membawa tanda negatif.

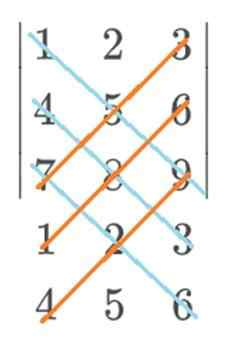
Dalam contoh ini, biru akan pergi dengan tanda positif dan merah dengan tanda negatif. Perhitungan terakhir dari aturan Sarrus akan tetap seperti ini:

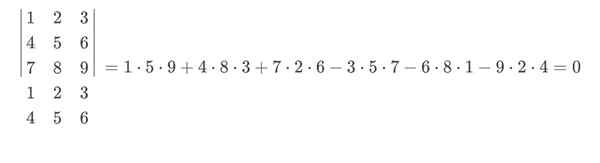
Teman-teman penentu

Penentu dimensi 1

Jika dimensi matriks adalah 1, matriks ini dengan cara ini: a = (a)

Oleh karena itu, penentunya adalah sebagai berikut: det (a) = | a | = a

Diringkas, penentu matriks A sama dengan nilai absolut matriks A, yang dalam hal ini adalah a.

Penentu dimensi 2

Jika kita pergi ke matriks dimensi 2, kita mendapatkan matriks dari jenis:

Dapat melayani Anda: taumaticgy

Di mana penentu didefinisikan sebagai:

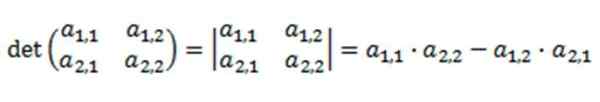
Resolusi penentu ini didasarkan pada perkalian diagonal utamanya, mengurangi produk dari diagonal terbaliknya.

Penentu dimensi 3

Jika dimensi matriks adalah 3, matriks yang dihasilkan akan dari jenis ini:

Penentu matriks ini akan diselesaikan melalui aturan Sarrus dengan cara ini:

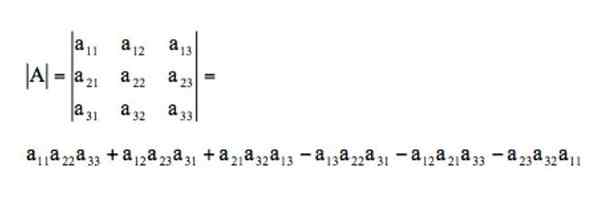
Referensi

1. Anthony Nicolaides (1994). Penentu & Matriks. Lulus publikasi.
2. M. Casteleiro Villalba (2004). Pengantar aljabar linier. Editorial ESIC.