Jenis bagian kerucut, aplikasi, contoh

Itu bagian kerucut Mereka adalah kurva yang diperoleh dengan mencegat pesawat dengan kerucut. Ada beberapa cara untuk melakukan ini; Misalnya, jika bidang dilewatkan secara tegak lurus ke sumbu aksial kerucut, keliling diperoleh.

Memiringkan pesawat sedikit sehubungan dengan sumbu aksial kerucut dan elips diperoleh, kurva yang ditutup, tetapi jika kita condongkan itu lebih banyak parabola atau hiperbola diperoleh, seperti yang dapat dilihat dalam animasi Gambar 1.

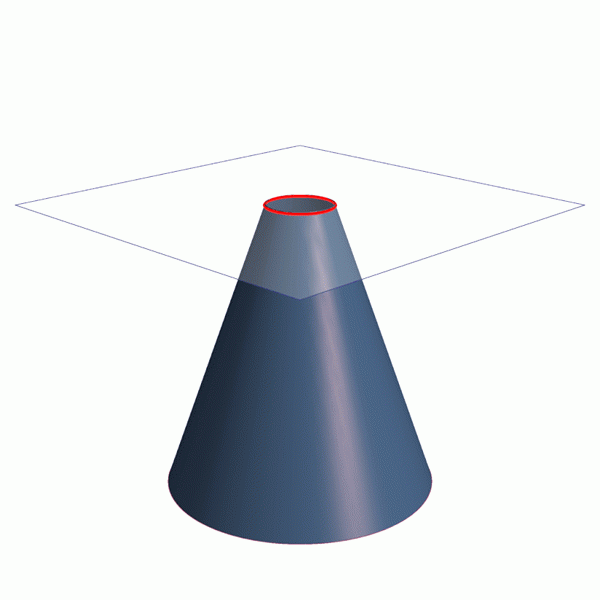Animasi yang menunjukkan cara mendapatkan empat bagian kerucut: keliling, perumpamaan dan elips hiperbola. Sumber: Wikimedia Commons. Baris / CC0

Bagian kerucut adalah bagian dari alam dan dunia di sekitar kita. Teknik, Arsitektur, dan Astronomi adalah cabang penting dari pengetahuan yang memanfaatkan kerucut.

[TOC]

Kondisi untuk bagian kerucut

Bagian kerucut didefinisikan sebagai tempat geometris yang memenuhi kondisi berikut:

Perumpamaan

Itu adalah tempat geometris dari semua titik yang terletak pada bidang yang sama ke titik tetap yang disebut fokus F dan garis lurus juga diperbaiki, dipanggil pengarahan.

Elips

Titik pesawat milik elips jika jumlah jarak antara titik itu dan dua titik tetap lainnya, disebut Fokus dan terletak di Sumbu Utama dari elips, tetap konstan.

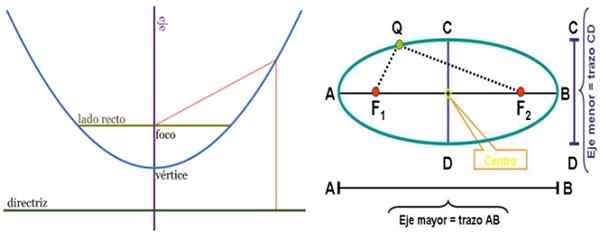Perumpamaan ke kiri dan elips ke kanan, dengan elemen masing -masing. Fokus adalah poin dengan banyak aplikasi. Sumber: Wikimedia Commons.

Lingkar

Ini adalah tempat geometris dari semua titik yang mempertahankan jarak yang sama ke titik lain yang disebut centro. Jarak ini adalah radio keliling.

Dapat melayani Anda: Euclidian Distance: Konsep, Formula, Perhitungan, Contoh

Hiperbola

Set poin di pesawat sedemikian rupa sehingga perbedaan antara jaraknya ke dua titik tetap yang disebut Fokus, itu konstan.

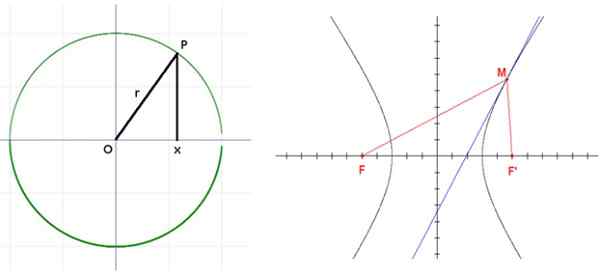Hiperbola dengan fokus f dan f. Sumber: Wikimedia Commons.

Aplikasi

Mari kita lihat beberapa aplikasi bagian kerucut:

Perumpamaan  

-Saat objek diluncurkan, lintasan yang mengikuti memiliki bentuk perumpamaan.

-Perumpamaan memiliki aplikasi teknik yang terkenal, misalnya di jembatan yang ditangguhkan kabel dengan cepat dalam bentuk perumpamaan.

-Perumpamaan juga bagus untuk membuat reflektor dan teleskop. Ini berkat properti yang menarik: Saat menempatkan luminer dalam fokus permukaan bagian transversal parabola, cahaya akan berjalan dalam sinar paralel ke sumbu perumpamaan.

-Jika sinar bercahaya sejajar dengan sumbu simetri mendekati permukaan parabola, ia memusatkan mereka dalam fokus, keadaan yang digunakan untuk membuat teleskop reflektor, seperti teleskop Hale de Monte Palomar Palomar.

Elips

-Planet -planet dari tata surya bergerak mengikuti lintasan elips, cukup dekat dengan keliling dalam kasus planet -planet besar, termasuk tanah tersebut. Matahari tidak ada di tengah, tetapi di salah satu lampu sorot.

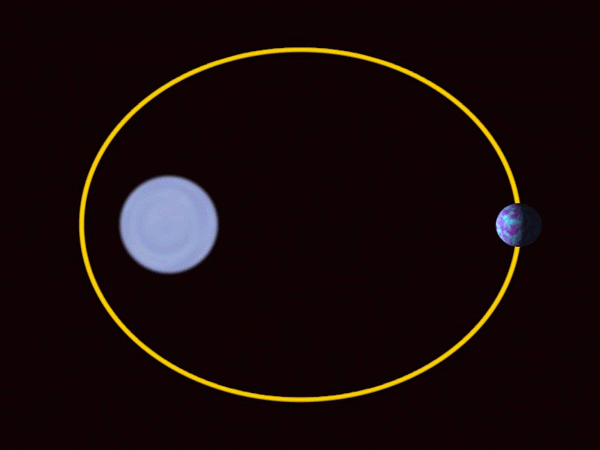Planet -planet tata surya bergerak dalam orbit elips dengan matahari di salah satu lampu sorot. Sumber: Wikimedia Commons.

-Elips ini banyak digunakan dalam arsitektur sebagai elemen dekoratif dan desain.

-Dengan menempatkan reflektor di salah satu lampu sorot elips, cahaya dipantulkan ke fokus lainnya. Hal yang sama terjadi dengan suara. Itulah sebabnya di aula berbentuk elips, yang berbicara diam -diam berada dalam satu fokus jelas didengar oleh pendengar yang terletak di fokus lainnya.

Itu bisa melayani Anda: prisma hepagonal

-Properti yang sama ini memiliki aplikasi yang mengejutkan di bidang kedokteran. Perhitungan ginjal dapat dihancurkan dengan suara. Gelombang USG dengan intensitas besar dihasilkan dalam salah satu fokus bak elips penuh air, dan pasien terletak di fokus lainnya. Gelombang suara mempengaruhi dan merefleksikan dalam perhitungan, dan dengan energinya mereka memecahnya dalam potongan -potongan kecil, yang kemudian dengan mudah dikeluarkan selama buang air kecil selama buang air kecil.

Hiperbolas

-Beberapa komet dalam tata surya mengikuti lintasan hiperbolik, selalu dengan matahari di salah satu fokus.

-Fokus hiperbolas juga sangat menarik untuk mempelajari fenomena refleksi gelombang. Misalnya, dengan mengarahkan sinar cahaya ke fokus cermin parabola, ia tercermin dalam fokus lain, properti yang sangat berguna untuk membangun teleskop, karena cahaya dapat fokus pada cermin parabola dan diarahkan ke tempat lain yang lebih tepat yang lebih tepat yang lebih tepat Menurut desain.

-Menara pendingin tanaman nuklir memiliki siluet berbentuk hiperbolas.

-Sebelum munculnya GPS, hiperbola digunakan dalam navigasi untuk menemukan kapal. Kapal -kapal yang dibawa dengan sinyal papan yang dikeluarkan secara bersamaan oleh stasiun radio A dan B dan komputer bertanggung jawab untuk mendaftarkan perbedaan waktu kedatangan sinyal, untuk mengubahnya menjadi perbedaan jarak jarak. Dengan cara ini kapal terletak di cabang hiperbola.

Prosedur ini diulangi dengan dua stasiun radio C dan D lainnya, yang menempatkan kapal di cabang Hiperbola lain. Posisi pasti perahu adalah persimpangan kedua hiperbolas.

Dapat melayani Anda: Fungsi Tumbuh: Cara Mengidentifikasi, Contoh, Latihan

Keliling

-Kedatangan roda mengubah arah sejarah.

-Gerakan melingkar sangat umum, banyak bagian berputar untuk menghasilkan berbagai efek, dari pabrik hingga kipas.

-Meskipun lintasan planet utama bersifat elips, lintasan melingkar adalah pendekatan yang baik dalam banyak kasus.

-Circunferences sering menjadi elemen dalam arsitektur, desain, teknik dan konstruksi. Daftar bentuk melingkar atau disk tidak ada habisnya: koin, cd, jam tangan dan banyak lagi.

Contoh

Lalu ada dua kerucut di pesawat, sebuah lingkaran dan elips.

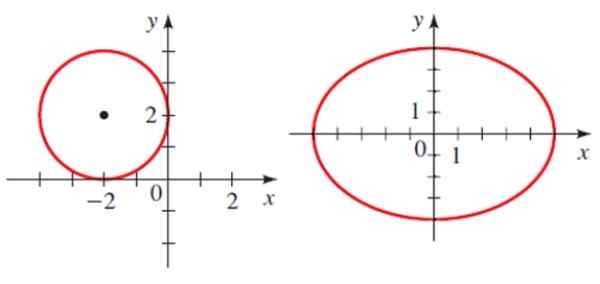Contoh bagian kerucut: lingkaran dan elips. Sumber: Stewart, J. Prekalkulasi.

Masing -masing memiliki persamaan analitik:

Lingkar

(X-H)² + (Y-K)² = R²

Di mana h dan k adalah koordinat pusat dan r adalah radio. Untuk keliling yang ditunjukkan pada gambar persamaannya adalah:

(x+2)² + (Y-2)² = 4

Elips

Persamaan elips yang pusatnya adalah titik koordinat (h, k):

[(X-h)² /ke² ]+ [(y-k)² /B² ] = 1

Dimana a dan b adalah semi -gilips dari elips. Untuk elips yang ditunjukkan, pusatnya berada pada titik 0,0, semi -semi terbesar yang sama adalah sama dan semije minor adalah 4. Oleh karena itu persamaannya adalah:

(X² /25)+ (dan² / 16) = 1

Referensi

1. Hoffman, J. Pemilihan masalah matematika. Volume 2.
2. Jiménez, r. 2008. Aljabar. Prentice Hall.
3. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
4. Wikipedia. Bagian kerucut. Pulih dari: is.Wikipedia.org.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.