Sifat Seri Fibonacci, Hubungan Alami, Aplikasi

Itu O seri Suksesi Fibonacci adalah urutan angka yang diperoleh dengan memulai dengan 0 dan 1, berlanjut dengan jumlah mereka: 0 + 1 = 1, lalu jumlah dari dua: 1 + 1 = 2 sebelumnya dan seterusnya.

Mengikuti prosedur ini, istilah lain diperoleh, mari kita lihat: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

Jumlah pertama dari seri Fibonacci

Prosedur ini diulang sebanyak yang Anda inginkan. Dengan cara ini, suksesi Fibonacci memperoleh bentuk: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Angka yang membuatnya disebut Nomor Fibonacci.

[TOC]

Sejarah

Suksesi Fibonacci disebut ahli matematika Italia yang hidup di Abad Pertengahan: Leonardo de Pisa, juga dikenal sebagai Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo menghabiskan masa kecil di Afrika Utara dan bepergian ke seluruh Mediterania, di mana dia tahu sistem penomoran indo -arabik dan senang dengannya. Mungkin guru -guru Arab Leonardo mengajarinya tentang suksesi, yang sudah dikenal oleh ahli matematika Hindu.

Selanjutnya, saat kembali ke Pisa Fibonacci menulis buku berjudul Liber Abaci (Kitab Abacus), di mana selain menyoroti keunggulan bilangan indo -arab dalam menghadapi penomoran Romawi dan memperkenalkan 0, ia mengangkat masalah tentang reproduksi kelinci.

Dan solusi untuk masalah ini adalah jumlah suksesi Fibonacci.

Leonardo de Pisa tidak dianugerahi penciptaan suksesi; Dia hanya menyebutkannya dalam bukunya sebagai rasa ingin tahu, yang menarik perhatian banyak sarjana yang mengikutinya. Di antaranya adalah ahli matematika Prancis abad ke -19 Edouard Lucas, yang ketika mempelajari suksesi membaptisnya dengan nama orang bijak abad pertengahan yang membuatnya dikenal di barat.

Masalah kelinci fibonacci

Masalahnya mengatakan: ada beberapa kelinci yang hidup selamanya, yang pada dua bulan subur. Setelah kedewasaan tercapai, mereka memiliki beberapa bayi dari jenis kelamin yang berbeda setiap bulan, yang juga membutuhkan waktu dua bulan untuk bereproduksi dan memiliki beberapa kelinci bulanan.

Dapat melayani Anda: hukum de morgan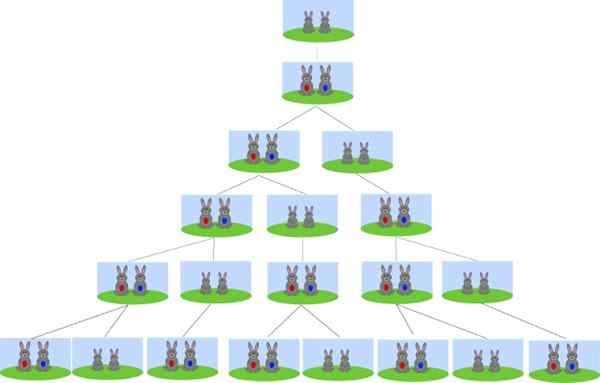Asal usul suksesi Fibonacci adalah masalah reproduksi kelinci. Sumber: Wikimedia Commons.

Dimulai dengan beberapa kelinci yang baru lahir, berapa banyak pasang kelinci dalam sebulan? Berapa banyak pasang kelinci setelah 2, 3 dan 4 bulan? Dan berapa banyak yang akan terjadi setelah 6 bulan?

Jawabannya adalah dalam nomor fibonacci. Setelah 1 bulan ada 1 pasang kelinci, pasangan asli, karena mereka hanya bereproduksi setelah 2 bulan.

Setelah 2 bulan ada 2 pasangan kelinci: pasangan asli dan sampah pertama mereka.

Pada 3 bulan, kami akan memiliki 3 pasangan, termasuk pasangan asli, sampah pertama mereka dan yang baru.

Setelah mencapai bulan ke -4, kami akan memiliki pasangan asli, sampah pertama yang pada gilirannya memiliki anak pertama mereka, sampah bulan ketiga dan sampah baru. Total 5 pasang kelinci.

Tetapi ini adalah jumlah dari urutan fibonacci, oleh karena itu setelah 6 bulan akan ada 13 pasangan kelinci, karena setiap bulan pasangan dari dua bulan sebelumnya ditambahkan.

Properti Seri Fibonacci

Berikut adalah beberapa sifat menarik dari suksesi Fibonacci.

Properti 1

Formula rekursif untuk menemukan ketentuan suksesi adalah:

ke_N+1 = a_N + ke_N-1  Untuk n lebih besar dari atau sama dengan 2.

Di mana n = 2, 3, 4, ... yaitu, untuk menemukan istilah ketujuh a₇, Kami melakukan n = 6, sehingga 6+1 = 7. Kita perlu mengetahui persyaratannya₅  sudah₆, dari daftar yang muncul di pengantar₅ = 5 dan a₆ = 8, oleh karena itu untuk₇ = 5+8 = 13.

Properti 2

Jika dua istilah yang ingin kami temukan tidak diketahui, maka kami dapat menggunakan formula berikut:

Itu dapat melayani Anda: Tesseldos: Karakteristik, Jenis (Reguler, Tidak Teratur), Contoh

Properti 3

Angka a_N sudah_N+1 adalah  Coprimos, yaitu, mereka adalah sepupu satu sama lain, yang berarti bahwa mereka tidak memiliki faktor umum yang sama.

Properti 4

Properti yang sangat menarik adalah hasil dari persyaratan untuk_2n sudah_N, yang bernilai 1, saat n = 1. Artinya:

ke₂ / ke₁ = 1

Kami dapat dengan mudah memeriksanya dengan daftar nomor fibonacci.

Di sisi lain, jika n ≠ 1, maka hasil bagi:

ke_2n / ke_N = a_N  + 2nd_N-1

Misalnya jika n = 3, maka a _2n = a₆ = 8 dan₃ = 2. Baiklah kalau begitu:

8/2 = 2 + 2. ke₂ = 2 + 2. 1

Memang: 8/2 = 4 dan 2 + (2.1) = 4. Dapat diverifikasi bahwa nilai n apa pun terpenuhi.

Properti 5

Rasio r_N = a_N+1 / ke_{N ,} Saat n menjadi hebat, konvergen ke Alasan emas salah satu Proporsi aurea, Bilangan irasional yang sering muncul di alam, diberikan oleh:

Hubungan alami dari suksesi fibonacci

Suksesi Fibonacci pada Tanaman

Manifestasi suksesi Fibonacci berlimpah di kerajaan tanaman

Cabang -cabang pohon tertentu keluar setiap tahun menurut suksesi Fibonacci. Tahun pertama bagasi tumbuh tanpa melempar cabang apa pun, setelah satu tahun menghasilkan satu dan karena setiap tahun. Pada gilirannya, setiap cabang dapat melempar yang baru setelah satu tahun, seperti halnya kelinci mereproduksi.

Pusat bunga bunga matahari berisi benih yang diatur dalam balok spiral logaritmik, dalam kedua arti, yang jumlahnya sesuai dengan dua angka fibonacci berturut -turut.

Jumlah fibonacci hadir dalam jumlah kelopak bunga bunga matahari dan margarit, serta dalam berbagai pola di mana tanaman memiliki daunnya.

Dapat melayani Anda: variabel ordinal

Para ahli mengatakan bahwa dengan cara ini tanaman mengoptimalkan ruang untuk daun dan bunga untuk memiliki pertumbuhan yang optimal.

Dengan titik sentral sebagai tempat awal, struktur ini tumbuh dan menerima sinar matahari, oleh karena itu daun dan kelopak baru harus menutupi sesedikit mungkin yang keluar. Dan cara terbaik untuk mencapai hal ini adalah dengan mengadopsi pola pertumbuhan dalam hal urutan fibonacci.

Suksesi Fibonacci pada Hewan

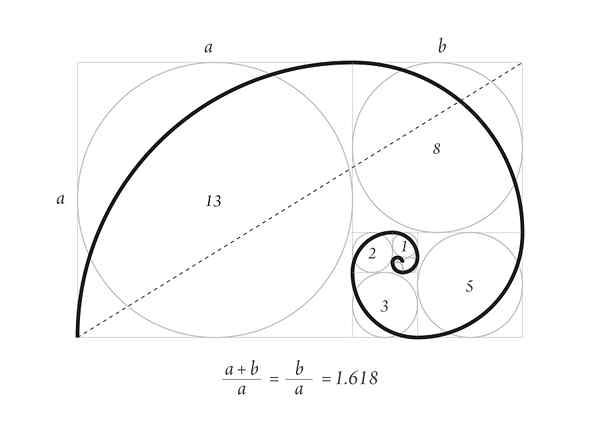Spiral Durero dengan jumlah pertama suksesi Fibonacci

Spiral tahan lama dari gambar superior adalah bagian dari pola pertumbuhan cangkang pada hewan laut dan tanduk beberapa ruminansia.

Mulailah dengan dua kotak 1, satu di atas yang lain, lalu persegi sisi 2 di sebelahnya, yang membentuk persegi panjang sisi 3, yang sisi -sisinya memiliki proporsi emas.

Di bawah ini adalah kuadrat sisi 3 dan ke kiri persegi sisi 5. Di atas ada persegi sisi 8 dan di sebelah kanan persegi sisi 13. Ini adalah jumlah pertama dari suksesi.

Akhirnya spiral ditarik dengan menyentuh titik -titik sudut kotak, seperti yang terlihat pada gambar.

Aplikasi

Suksesi Fibonacci diterapkan di berbagai bidang:

-Dalam seni proporsi emas yang terkait dengan suksesi Fibonacci muncul pada orang dan hal -hal yang diwakili oleh seniman hebat seperti Leonardo da Vinci, Miguel ángel dan Alberto Durero.

-Proporsi mitra di Athena juga menanggapi nomor emas.

-Dalam komposisi Mozart, Beethoven, Schubert dan Debussy.

-Untuk merancang benda -benda yang proporsinya terlihat harmonis bagi mata manusia, seperti kartu kredit, wadah, bendera.

-Di pasar saham digunakan untuk memprediksi harga apa yang mengembalikan trennya.

Referensi

1. Suksesi Fibonacci. Pulih dari: blogeducastur.adalah.
2. Stewart, J. 2007. Prekalkulasi. Ke -5. Edisi. Pembelajaran Cengage.
3. Vargas, m. Aplikasi Suksesi Fibonacci. Dipulihkan dari: MATESUP.Cl.
4. Wikipedia. Nomor Fibonacci. Diperoleh dari: di.Wikipedia.org.