Konsep gelombang linier, karakteristik, contoh

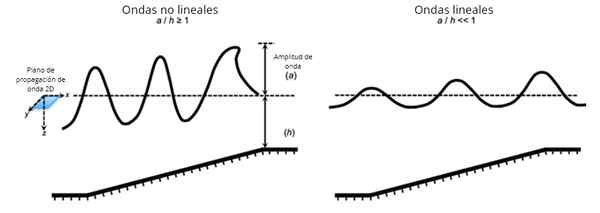
Itu Gelombang linier Ini adalah yang ada di mana prinsip superposisi berlaku, yaitu, di mana bentuk gelombang dan evolusi ruang-waktu dapat dicapai sebagai jumlah solusi dasar, misalnya jenis harmonik. Tidak semua gelombang memenuhi prinsip superposisi, yang tidak mematuhi itu disebut gelombang non-lineal.

Denominasi "linier" berasal dari fakta bahwa gelombang linier selalu memenuhi persamaan diferensial dalam turunan parsial, di mana semua istilah yang melibatkan variabel dependen atau turunannya dinaikkan ke kekuatan pertama.

Gelombang yang terlihat di kejauhan adalah gelombang linier, namun gelombang yang ketakutan dari latar depan adalah non-lineal. Sumber: Pixabay.

Di sisi lain, gelombang non-lineal memenuhi persamaan gelombang yang memiliki derajat kuadratik atau lebih tinggi dalam variabel dependen atau dalam turunannya.

Kadang -kadang bingung untuk gelombang linier dengan gelombang longitudinal, yang merupakan yang ada di mana getaran terjadi dalam arah propagasi yang sama, seperti gelombang suara.

Tetapi gelombang longitudinal, serta transversal, pada gilirannya bisa linier atau non-linear tergantung pada, di antara faktor-faktor lain, amplitudo gangguan awal dan lingkungan di mana mereka menyebar.

Secara umum terjadi bahwa ketika gangguan awal dari amplitudo kecil, persamaan yang menggambarkan perambatan gelombang, adalah tipe linier atau dapat dilapisi dengan pendekatan tertentu, meskipun tidak selalu demikian.

[TOC]

Persamaan diferensial dalam gelombang linier

Dalam media linier, bentuk gelombang terbatas dalam ruang dan waktu dapat diwakili dengan jumlah fungsi gelombang sinus atau cosinus dari frekuensi dan panjang gelombang yang berbeda melalui seri Fourier. 

Gelombang linier selalu memiliki persamaan diferensial dari tipe linier yang terkait, yang solusinya mewakili prediksi dari apa yang akan menjadi gangguan pada saat -saat posterior gangguan awal yang terletak secara spasial pada instan awal awal.

Persamaan gelombang linier klasik, dalam dimensi spasial tunggal, yang solusinya adalah gelombang linier adalah:

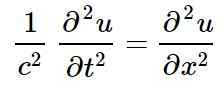
Dalam persamaan sebelumnya atau mewakili gangguan jumlah fisik tertentu di posisi tersebut X Dan saat ini T, artinya atau Itu adalah fungsi dari X Dan T:

Itu bisa melayani Anda: apa itu vektor coplanares? (Dengan latihan terpecahkan)

u = u (x, t)

Misalnya, jika itu adalah gelombang suara di udara, atau Itu dapat mewakili variasi tekanan sehubungan dengan nilainya tanpa mengganggu.

Dalam kasus gelombang elektromagnetik, atau mewakili medan listrik atau medan magnet yang berosilasi tegak lurus ke arah propagasi.

Dalam kasus tali tegang, atau mewakili perpindahan silang sehubungan dengan keseimbangan keseimbangan tali, seperti yang ditunjukkan pada gambar berikut:

Bentuk gelombang dalam sekejap tertentu, dalam kasus gelombang linier bentuk ini adalah tumpang tindih gelombang sinusoidal dari frekuensi dan panjang gelombang yang berbeda. Sumber: f. Zapata.

Solusi persamaan diferensial

Jika Anda memiliki dua atau lebih solusi dari persamaan diferensial linier, maka setiap solusi dikalikan dengan konstanta akan menjadi solusi dan juga akan menjadi jumlah dari mereka. 

Tidak seperti persamaan non-linear, persamaan wavelin mengakui solusi harmonik dari jenis: 

atau₁= A⋅sen (k⋅x - ω⋅t) Dan atau₂= A⋅sen (k⋅x + Ω⋅t) 

Ini dapat diverifikasi dengan substitusi sederhana dalam persamaan gelombang linier.

Solusi pertama mewakili gelombang progresif yang maju ke kanan, sedangkan yang kedua ke kiri dengan cepat C = Ω/k.

Solusi harmonik adalah karakteristik dari persamaan gelombang linier.

Di sisi lain, kombinasi linier dari dua solusi harmonik juga merupakan solusi untuk persamaan gelombang linier, misalnya: misalnya:

u = a₁ cos (k₁⋅x - Ω₁⋅t) + a₂ tenggelam₂⋅x - Ω₂⋅t) adalah solusi.

Karakteristik gelombang linier yang paling relevan adalah bahwa segala bentuk gelombang, betapapun kompleksnya, dapat diperoleh dengan jumlah gelombang harmonik sederhana di payudara dan cosinus:

u (x, t) = a₀ + ∑_N KE_N cos (k_N⋅x - Ω_N⋅t) + ∑_M B_M tenggelam_M⋅x - Ω_M⋅t).

Gelombang linier dispersif dan non -dispersif

Dalam persamaan gelombang linier klasik, C mewakili kecepatan propagasi denyut nadi.

Gelombang non -dispersif

Dalam kasus di mana C Ini adalah nilai konstan, misalnya gelombang elektromagnetik dalam kekosongan, kemudian pulsa pada saat awal t = 0 Membentuk f (x) Itu menyebar menurut:

u (x, t) = f (x - c⋅t)

Tanpa menderita distorsi apa pun. Ketika ini terjadi, dikatakan bahwa media tidak desain.

Gelombang dispersif

Namun, dalam media dispersif, kecepatan C dapat tergantung pada panjang gelombang λ, yaitu: C = C (λ).

Dapat melayani Anda: persamaan kontinuitas

Gelombang elektromagnetik dispersif saat bepergian melalui media material. Juga gelombang permukaan air bergerak dengan kecepatan yang berbeda sesuai dengan kedalaman air.

Kecepatan gelombang harmonik merambat A⋅sen (k⋅x - Ω⋅t) adalah Ω/k = c dan kecepatan fase disebut. Jika medianya dispersif, maka C Itu adalah fungsi bilangan gelombang k: C = c (k), Di mana k Itu terkait dengan panjang gelombang dengan cara K = 2π/λ.

Hubungan dispersi

Hubungan antara frekuensi dan panjang gelombang disebut rasio dispersi, yang diungkapkan dalam hal frekuensi sudut Ω dan nomor gelombang k adalah: Ω = C (k) ⋅K.

Beberapa karakteristik hubungan dispersi dari gelombang linier adalah sebagai berikut:

Dalam gelombang di mana panjang gelombang (jarak antar punggung) jauh lebih besar dari kedalaman H, Tetapi luasnya jauh lebih sedikit daripada kedalaman hubungan dispersi adalah:

Ω = √ (gh) ⋅k

Dari sana disimpulkan bahwa mereka menyebar dengan kecepatan konstan √ (GH) (setengah non -dispersif).

Tetapi gelombang di perairan yang sangat dalam bersifat dispersif, karena rasio dispersi mereka adalah:

Ω = √ (g/k) ⋅k

Ini berarti kecepatan fase itu Ω/k Itu bervariasi dan tergantung pada bilangan gelombang dan oleh karena itu panjang gelombang gelombang.

Kecepatan grup

Jika dua gelombang linier harmonik tumpang tindih tetapi maju pada kecepatan yang berbeda, maka kecepatan grup (yaitu, dari paket gelombang) tidak cocok dengan kecepatan fase.

Kecepatan grup v_G Ini didefinisikan sebagai turunan frekuensi sehubungan dengan angka gelombang dalam rasio dispersi: v_G = Ω '(k).

Gambar berikut menunjukkan tumpang tindih atau jumlah dari dua gelombang harmonik atau₁= A⋅sen (k₁⋅x - Ω₁⋅t) Dan atau₂= A⋅sen (k₂⋅x - Ω₂⋅t) Perjalanan dengan kecepatan yang berbeda v₁= Ω₁/k₁ Dan v₂= Ω₂/k₂. Perhatikan bagaimana kecepatan kelompok berbeda dari kecepatan fase, dalam hal ini kecepatan grup ∆Ω/∆K.

Itu dapat melayani Anda: sifat magnetik bahan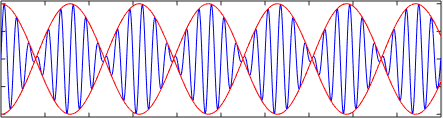Gelombang linier (biru) dalam media dispersif. Kurva merah telah ditambahkan untuk menyoroti bahwa kecepatan grup berbeda dari kecepatan propagasi

Tergantung pada rasio dispersi, kecepatan fase dan kecepatan kelompok, dalam arah yang berlawanan, bahkan dapat memiliki arah yang berlawanan.

Contoh gelombang linier

Gelombang elektromagnetik

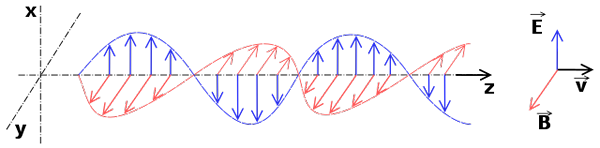gelombang elektromagnetik yang membentuk radiasi elektromagnetik

Gelombang elektromagnetik adalah gelombang linier. Persamaan gelombangnya disimpulkan dari persamaan elektromagnetisme (persamaan maxwell) yang juga linier.

Persamaan Schrödinger

Ini adalah persamaan yang menggambarkan dinamika partikel pada skala atom, di mana karakteristik bergelombang relevan, misalnya kasus elektron dalam atom.

Maka "gelombang elektron" atau fungsi gelombang seperti yang disebut juga, adalah gelombang linier.

Gelombang di air yang dalam

Gelombang linier juga di mana amplitudo jauh lebih rendah dari panjang gelombang dan panjang gelombang jauh lebih besar dari kedalaman. Gelombang di dalam air dalam mengikuti teori linier (dikenal sebagai teori bergelombang Airy).

Namun, gelombang yang mendekati pantai dan membentuk puncak karakteristik yang digulung (dan para peselancar mencintai) adalah gelombang non -linier.

Suara

Karena suara adalah gangguan kecil tekanan atmosfer, itu dianggap sebagai gelombang linier. Namun, gelombang kejut ledakan atau muka gelombang bidang supersonik, adalah contoh gelombang non -linier yang khas.

Gelombang pada tali tegang

Gelombang yang menyebar melalui tali tegang adalah linier, asalkan denyut nadi awal kecil, yaitu, batas elastis tali tidak terlampaui.

Gelombang linier pada senar tercermin pada ujungnya dan tumpang tindih, menimbulkan gelombang stasioner atau mode getaran yang memberikan nada harmonik dan subarmonik karakteristik instrumen string.

Referensi

1. Griffiths G dan Schiesser W. Gelombang linier dan nonlinier. Pulih dari: shololarpedia.org.
2. Whitham g.B. (1999) "Gelombang linier dan nonlinier". Wiley. 
3. Wikipedia. Gelombang non -linear. Pulih dari: is.Wikipedia.com
4. Wikipedia. Akustik nonlinier. Diperoleh dari: di.Wikipedia.com
5. Wikipedia. Ombak. Diperoleh dari: di.Wikipedia.com
6. Wikiwaves. Gelombang nonlinier. Pulih dari: gelombang wiki.org